SPSS之单因素方差分析

一 单因素方差分析原理

即比较不同组别的平均值有没有差异。比如我想比较1/2/3三个班的平均年龄有没有差异，就是个很典型的单因素方差分析案例，因素只有班级这一个。

方差分析认为，观测变量的变动会受到因素变量和随机变量两方面的影响。

观测变量的总变动用总离差平方和（SST）表示，

将其分解为组间离差平方和（SSB）

和组内离差平方和（SSE）。

其中，

SSB由于因素变量的不同水平而引起的观测变量的变动（也称系统误差）；

SSE是由于随机因素而引起的观测变量的变动。

SST=SSA+SSE

1.单因素方差分析的理论假设：

(1)各处理下的样本是随机的。

(2)各处理下的样本是相互独立的。

(3)各处理下的样本分别来自服从正态分布的总体。

    所以先要进行正态分布的检验，

如果不服从，处理办法

• 进行log等转换，再次看是否满足正态分布，如满足进行参数检验
• 剔除异常值后，再次看是否满足正态分布，如满足进行参数检验
• 进行非参检验

原文链接：https://blog.csdn.net/twocanis/article/details/125192298，（服从 不服从）

(4)各处理下的样本所属总体的方差相等。

对数据进行正态检验后，不满足正态分布，选用非参检验（为方便演示下面用另一组数据）：

2.单因素方差分析的基本步骤：

(1)建立假设；

(2)计算样本均值；

(3)计算总样本均值；

(4)计算样本方差；

(5)计算总体方差的组间估计；

(6)计算总体方差的组内估计；

(7)给定显著性水平α；

(8)计算F统计量的值；

(9)编制方差分析表。

(10)做出统计决策。

P＞0.05表示几个组别方差是齐的，没有显著差异，P＜0.05表示有显著差异

3.单因素方差中的多重比较

如果经过上述步骤推断总体均值之间存在显著差异，接下来的问题就是确定自变量的不同水平对因变量的影响程度如何，其中哪些水平的作用明显区别于其他水平，哪些水平的作用不显著。这就要用到多重比较的分析方法。

原文链接：https://blog.csdn.net/qq_52862974/article/details/128791589

二 SPSS实现单因素方差分析

1 导入数据

设置变量

数据如下：

2.30	A
2.32	A
2.40	A
2.45	A
2.58	A
2.35	B
2.30	B
2.42	B
2.60	B
2.35	B
2.20	C
2.00	C
1.90	C
2.10	C
2.03	C
2.54	D
2.61	D
2.60	D
2.57	D
2.54	D

2 变量类型转换

由于单因素自变量要求是数值型变量，数据不满足模型要求（是字符串），先进行自动重新编码。

编码之后：（字符串——数值，之后就对brand_new进行处理）

3 方差齐性检验和单因素方差分析

这两个步骤可以一起弄，SPSS有提供相关方法（分析--比较平均值--单因素ANOVA）

（1）要勾选项中的方差齐性检验，

（2）自变量和因变量不要搞错了，因为如果所有绝对偏差在每个单元格中为常量（某个定值，如果品牌为因变量，那绝对偏差有很多0）。无法计算莱文F统计。

（3）结果显著性0.332大于显著性水平0.05，所以各水平满足方差齐性

（4）单因素方差分析显著性P=0，P小于显著性水平a=0.05，拒绝零假设，认为控制变量不同水平下各总体均值有显著差异（P＜0.05）

4 多重比较检验

当不同水平下各总体均值有显著差异可继续进行多重比较检验。

多重比较检验：单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响，多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何，那个水平显著，哪个不显著。

其中：

LSD法：实际上就是t检验的变形，只是在变异和自由度的计算上利用了整个样本信息，因此仍然存在放大一类错误的问题

雪费Scheffe法：当各组人数不相等，或者想进行复杂的比较时，用此法较为稳妥。但它相对比较保守

S-N-K法：是运用最广泛的一种两两比较方法。它采用Student Range 分布进行所有各组均值间的配对比较。该方法保证在H0真正成立时总的α水准等于实际设定值，即控制了一类错误

图基Tukey法：对一、二类问题控制得很好，首选

邦弗伦尼Bonferroni法：LSD法的改进，有效控制假阳性（第一类错误）

5 参数估计和对比系数矩阵

（分析 —— 一般线性模型 —— 选项）

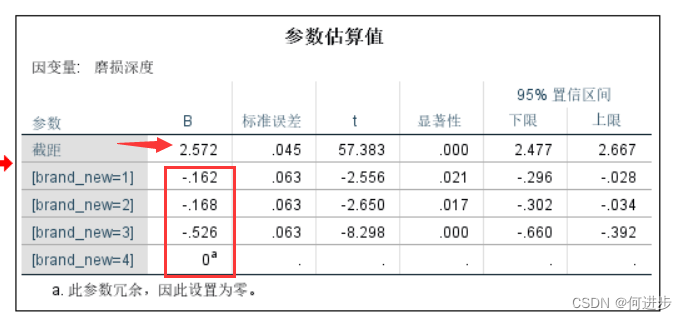
参数估计要结合对比系数矩阵来查看，

上图框红框证明是第一个和第四个做比较

参数估计中brandnew4 = 0，证明以第四个品牌为参考水平均值，其均值就等于截距2.572

brandnew1 = -0.162，所以brandnew1的均值为水平均值为2.572-0.162

三 SPSS导出数据分析表格

1 在输出界面，鼠标右键选择导出

2 选择路径，确定即可