机器人运动轨迹学习——GMM/GMR算法

机器人运动轨迹学习——GMM/GMR算法

• 前置知识

  GMM的英文全称为：Gaussian mixture model，即高斯混合模型，也就是说，它是由多个高斯模型进行混合的结果：当然，这里的混合是带有权重概念的。

  • 一维高斯分布

    GMM中的个体就是高斯模型，说认真点就是高斯基函数，它还有另一个名字，径向基函数。

    对于一维变量，其高斯分布为：

    

    对应高斯概率密度的图形：

    

    也就是说，对于一维变量x，它落在均值区间$[u-\sigma ,u+\sigma ]$的概率为68.26%

  • 多维高斯分布

    多维 Gaussian 分布的概率密度函数为：

    

    其中$\mu$为均值向量，$\Sigma$为协方差矩阵

• GMM对复杂轨迹的拟合

  一个复杂运动的表达式可由一系列简单信号的加权组合表述，我们称这些简单信号为基函数；

  一些流行的基函数有：Radial Basis Functions (RBFs)，Bernstein Basis Functions，Fourier Basis Functions

  其中，Radial Basis Functions (RBFs)，即径向基函数，一种应用如下图所示：通过为各基函数赋予不同的权重，生成了一条相对复杂的轨迹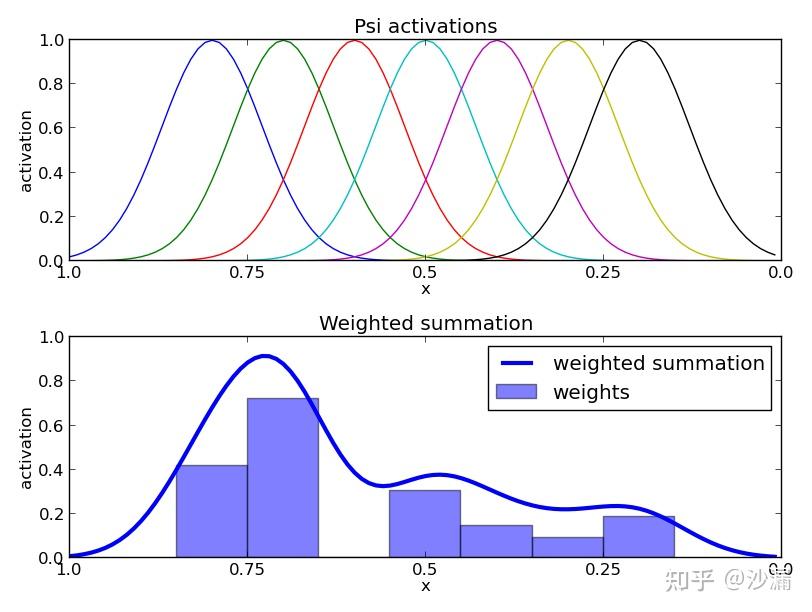

  

  图片源自：Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com)

• GMR的回归思想

  GMR（Gaussian mixture regression）的思想：

  对于一个输入，借用GMM进行回归，回归的结果是一个高斯分布，

  也就是说，我们回归得到的结果不是一个固定的值，而是一个概率值

  以一维高斯分布为例：

  

  我们回归得到的结果其均值为$\mu$，在$[u-\sigma$