使用物理信息神经网络求解二维热扩散方程实例

最近看了很多偏文献，对物理信息神经网络有一点了解，然后自己也做了一点实例练练手，以下是其中的一个例子，效果一般，如果有大佬觉得我哪里做得不对的话或者哪里需要改进的，希望能给点建议。

物理信息神经网络

物理信息网络，简称PINN，是一种应用神经网络来近似解决物理问题的方法，其独特之处在于将物理原理（通常通过偏微分方程进行数学表达）作为先验知识融入到神经网络的训练中。在训练过程中，PINN不仅会根据数据进行调整，还会受到物理定律的约束，从而确保学习到的结果既能够拟合数据，又能够符合物理定律。下面简单说一下物理信息神经网络的结构。

网络构架

神经网络架构：PINN通常由一个深度神经网络构成，其架构可以根据问题的复杂性进行选择。对于许多PINN应用，一个全连接的深度神经网络足以起始。如果问题涉及到图像或空间数据，可能需要使用卷积神经网络（CNNs）等更复杂的结构。
损失函数：PINN的损失函数是关键部分，它由两个主要组成部分构建：数据驱动损失和物理损失驱动。数据驱动损失用于衡量模型预测与观测数据之间的差异，而物理损失驱动则用于衡量模型预测与物理定律之间的差异。通过最小化这两个损失项，PINN可以确保预测结果既符合数据又符合物理定律。
物理信息网络结构图如下图所示：

简单来说，就是将与物理规律有关的方程作为网络的损失，一般这个方程是偏微分方程。我们知道，对于没有给定初始条件的偏微分方程的解是有无穷多个的，因此，我们在训练的时候，会将一部分初始条件（边界条件，以下称为边界条件）也作为网络的损失，一同优化整个网络。

简述二维热扩散方程

这里我们就直接给出二维热扩散方程的偏微分方程：
$$\frac{\partial T}{\partial t}=k(\frac{{\partial }^{2}T}{{\partial }^{2}x}+\frac{{\partial }^{2}T}{{\partial }^{2}y})$$

参数说明

T：温度场
t：时间
(x,y)：空间坐标

问题描述

给定初始的温度分布图如下,方框大小为1×1：

在y=0以及x=0的位置上温度为100°，其他地方均为0°，取k=1。
因此，对于物理场T(x,y,t)可知边界条件为
$$\begin{gathered} T(0,y,0)=100,T(x,0,0)=100 \\ T(x,y,0)=0,x,y\in (0,1) \end{gathered}$$
使用神经网络f(x,y,t)去逼近温度场T，网络层数为5层隐藏层，每层隐藏层神经元100个，输入神经元3个，对应输入空间坐标(x,y)，和时间t，输出为单个T。基于以上信息可知网络损失为
$$SSE=SS{E}_f+SS{E}_b$$
其中$SS{E}_f$为偏微分损失，$SS{E}_b$为边界损失
由已知信息定义为：
偏微分损失：
$$SS{E}_f=\frac{1}{N}\sum |\frac{\partial f}{\partial t}-(\frac{{\partial }^{2}f}{{\partial }^{2}x}+\frac{{\partial }^{2}f}{{\partial }^{2}y}){|}^2$$
边界损失：
$$SS{E}_b=\{\begin{array}{cc}& \frac{1}{N}\sum |f(x,y,0)-100{|}^2,x=0或y=0\\ & \frac{1}{N}\sum |f(x,y,0)-0{|}^2,x,y\in (0,1)\end{array}$$

效果

与FDTD所计算的效果进行对比，FDTD方法可参考链接:基于MATLAB的有限差分法求解二维瞬态热传导方程，所得结果为最终稳态温度场状态，如图：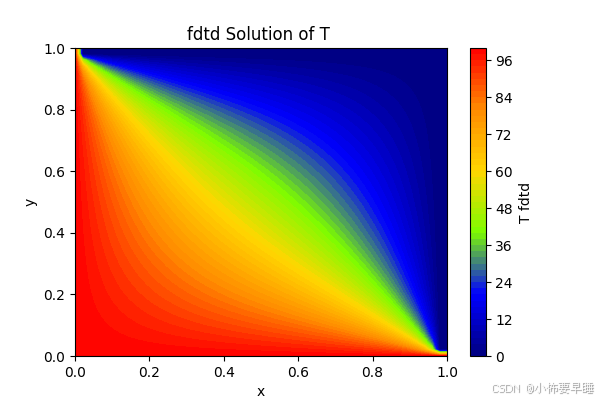
对于PINN可以得到关于1秒钟内的温度变化场，效果如下图：

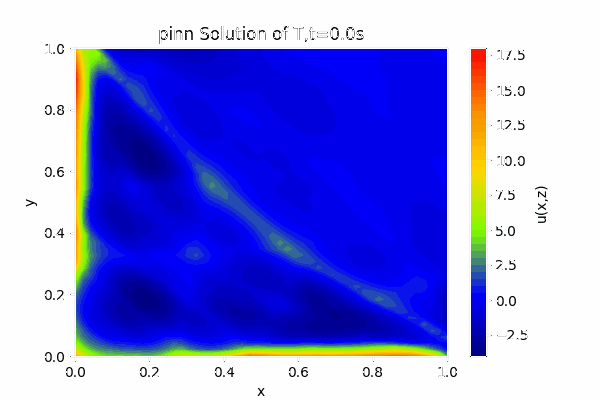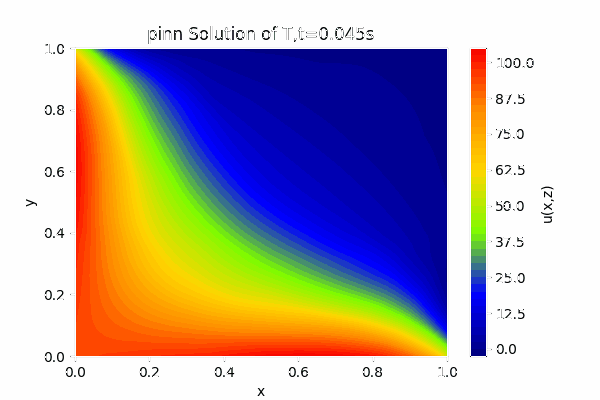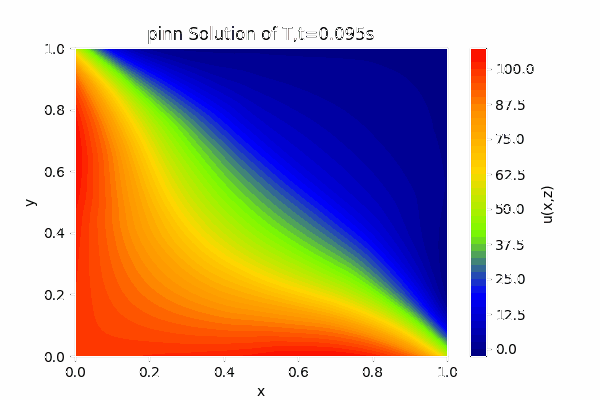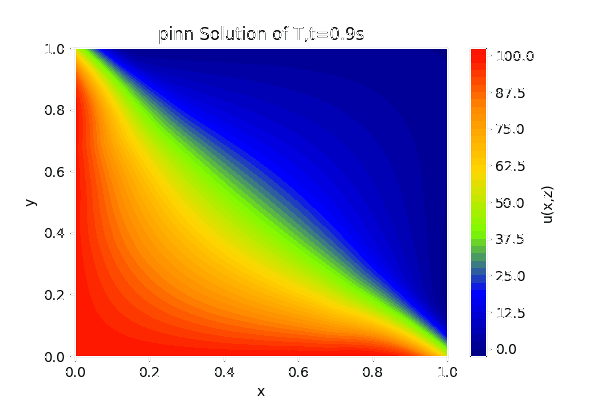
最终稳态效果为：

与FDTD所计算的误差图为：

总结

可以看出，效果一般，是因为训练次数有限，理论上来讲，训练次数达到一定程度时，pinn解可以无限逼近真实解。与其他方法对比，pinn是无网络方法，可以用少量的数据点得到更广泛的效果图。
以上是这篇博客内容，需要代码的可以联系我（不是买课的！！！！遇到好多博主说是可以免费分享代码，结果后面都是买课的。。。。）。