23考研李林880第九章曲线积分与曲面积分综合题3-20

视频讲解：23考研李林880第九章曲线积分与曲面积分综合题3-20

题目

设$f(x,y)$在$D=\left\{\left(x,y\right)|x^2+y^2\le 1\right\}$上有二阶连续偏导数，且$\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}=e^{-\left(x^2+y^2\right)}$，计算$I=\underset{D}{\iint }\left(x\frac{\partial f}{\partial x}+y\frac{\partial f}{\partial y}\right)dxdy$

解答

将二重积分做极坐标代换
$$\underset{D}{\iint }\left(x\frac{\partial f}{\partial x}+y\frac{\partial f}{\partial y}\right)dxdy={\int }_0^{2\pi }d\theta {\int }_0^1\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)\cdot rdr$$
交换积分次序，先对$\theta$进行积分，然后将一个$r$移到外积分上
$${\int }_0^{1}dr{\int }_0^{2\pi }\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)\cdot rd\theta ={\int }_0^{1}rdr{\int }_0^{2\pi }\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)d\theta$$
先来计算内积分，这里r为定值
$${\int }_0^{2\pi }\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)d\theta$$
由弧长公式可得$r\cdot d\theta =ds$（这里$ds$其正负视为与$d\theta$的正负相对应），如图所示，所以对角度$\theta$的积分可以转换为对半径为r的圆弧的线积分，该圆弧记为L，并且由于角度$\theta$是从$0$到$2\pi$变化的吗，所以L是以$(r,0)$为起点逆时针绕一圈再回到终点$(r,0)$

$$\therefore {\int }_0^{2\pi }\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)d\theta ={\int }_L\left(\frac{\partial f}{\partial x}\cdot \cos \theta \cdot ds+\frac{\partial f}{\partial y}\cdot \sin \theta \cdot ds\right)$$
由于$ds$是很小一段的弧长，所以可以认为是和圆弧相切的，以$ds$为斜边做一个直角三角形

放大看

可得$ds\cdot \sin \theta =-dx$(为什么会有负号要注意x的变化和前面角度的变化相对应)，$ds\cdot \cos \theta =dy$
$$\therefore {\int }_L\left(\frac{\partial f}{\partial x}\cdot \cos \theta \cdot ds+\frac{\partial f}{\partial y}\cdot \sin \theta \cdot ds\right)={\int }_L\left(\frac{\partial f}{\partial x}dy-\frac{\partial f}{\partial y}dx\right)$$
其实这里也可以通过做圆弧的单位法向量$\vec{n}=(cos\theta ,sin\theta )$（方向向外），如图所示，然后将其逆时针旋转90°再乘以$ds$获得对应的$dx,dy$分量

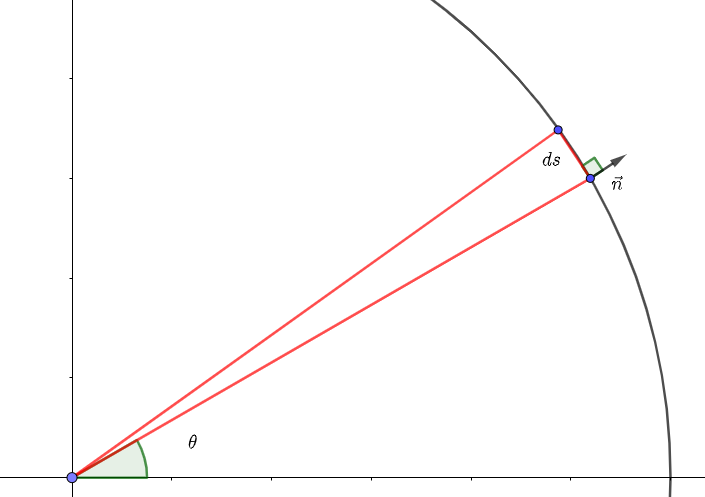
当然还可以套用方向余弦的那个公式进行两类积分的转换，其中$\theta$是与y轴的夹角，与x轴的夹角就是$\theta +\frac{\pi }{2}$，则$\cos \left(\theta +\frac{\pi }{2}\right)=-\sin \theta$

然后，我们对于那个线积分的计算可以用格林公式，记曲线L围成的区域为$D_L$
$$\therefore {\int }_L\left(\frac{\partial f}{\partial x}dy-\frac{\partial f}{\partial y}dx\right)=\underset{D_L}{\iint }\left(\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}\right)dxdy$$
带入题目所给的条件得
$$\underset{D_L}{\iint }\left(\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}\right)dxdy=\underset{D_L}{\iint }{e}^{-\left(x^2+y^2\right)}dxdy$$
做极坐标变换，注意积分区域是半径为$r$的圆，为了避免和被积函数中的混淆，被积函数中采用$\rho$来表示极径，即x与y是做的如下代换
$$\{\begin{array}{l}x=\rho \cos \theta \\ y=\rho \sin \theta \end{array}$$

$$\underset{D_L}{\iint }{e}^{-\left(x^2+y^2\right)}dxdy={\int }_0^{2\pi }d\theta {\int }_0^r\rho e^{-{\rho }^2}d\rho =-\pi \left(e^{-r^2}-1\right)$$

我们这里算得的是内积分，即
$${\int }_0^{2\pi }\left(r\cos \theta \cdot \frac{\partial f}{\partial x}+r\sin \theta \cdot \frac{\partial f}{\partial y}\right)d\theta =-\pi \left(e^{-r^2}-1\right)$$
再算外积分

$${\int }_0^1-\pi \left(e^{-r^2}-1\right)\cdot rdr=\frac{\pi }{2}{e}^{-1}$$