前言
干robocon的时候闲得慌,看看门狗军团里边那个小六足挺帅的,然后拍了一下大腿就决定开始做六足这个项目了,这篇文章主要分享一下关于六足的正运动学和逆运动学。
如何入门
在打算做六足的时候,我还只是一个单纯的做控制(也只是做全向轮底盘运动控制之类的)的学生,为了六足(毕竟自己设计的东西才帅,要是用了别人的机构和公式,总感觉有种ntr那味emm)自学了建模和matlab。
- 学习《机器人学导论》,了解DH参数和他们的意义以及应用
- 学好线性代数,毕竟运算几乎都是矩阵运算
- 会使用matlab(但是千万千万不要用他来求解析解!)
我这里的求解是针对一条腿的求解,因为如果以机器人中心为坐标原点,加上offset,整个公式会复杂很多倍,所以建议先把一条腿的做出来,怎么反推到绝对坐标系可以后期处理。
正运动学
首先是对着自己设计的机械模型,获取对应的dh参数,至于dh参数如何确定,建议自己百度。我这边是自己用sw画的全部结构,整体的dh参数就很好获取。

把这些参数代入matlab,基本就是这样

累积起来就可以得到末端的坐标和姿态,即

由于前面的旋转矩阵太长了,只截取了坐标这一列,于是可以得到正运动学解如下
以上就是一条腿的正运动学解析。
逆运动学
首先需要设置一个末端坐标矩阵,我设置为
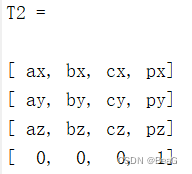 (这样就可以把xyz列入公式了)
(这样就可以把xyz列入公式了)
由上面求正运动学的公式可知
那么很容易得知
从matlab上运算可得等式左右两边的矩阵


由等式第四列来列方程获取运动学逆解,有
(1-1)
(1-2)
(1-3)
首先由(1-3)可以得到
(这个其实有限制条件,当px = 0时q1 = 90°,不过一般来说,六足是绝对扭不到这个角度的,故可以无视)
由(1-2)和(1-3)联立可得q2和q3,你可以看到我列方程的时候做了一些处理,接下来还有处理需要做,令
方程可以化简为
方程两边同时平方,相加,有
令
则可将方程化简为
既然你都会上csdn了,那么我相信这个方程你一定能够解出来吧(笑)
最终求得的结果就是
是不是非常简单?这个公式你就已经可以放进你的单片机或者是别的系统里了,通过输入xyz的坐标就能自动推出逆解,达到对应的坐标。
结语
其实作为一个机电的学生,做这个还是很挑战自己的,写这篇文章就当写了个日记吧,求这个逆解确实是花了不少时间。从只会嵌入式编程,到自学solid works建模,用3D打印机打出自己的第一个模型,再到学习机器人学导论,用matlab仿真机械臂的运动,一路上感觉学到了不少。当第一次把正运动学求出的结果和solid works实际的的距离完全相等的时候,那种开心简直难以言喻,实在是非常有趣的过程。
一路上并不是学到的全部都用上,也走了不少歪路,学会用platformio和micropython写esp32和树莓派pico以后,发现还是stm32最好使,这引脚数什么的,做机器人这块果然还得是stm家的芯片好使啊(笑)
写这篇文章是因为当时求逆解碰了不少歪路,把各种视频全都看了一遍,网上也没人写怎么求这种三轴机械臂的逆解(可能是我太菜了,勿喷),希望对看到这篇文章的人有一些的帮助吧XD(附个自己设计的六足的图)
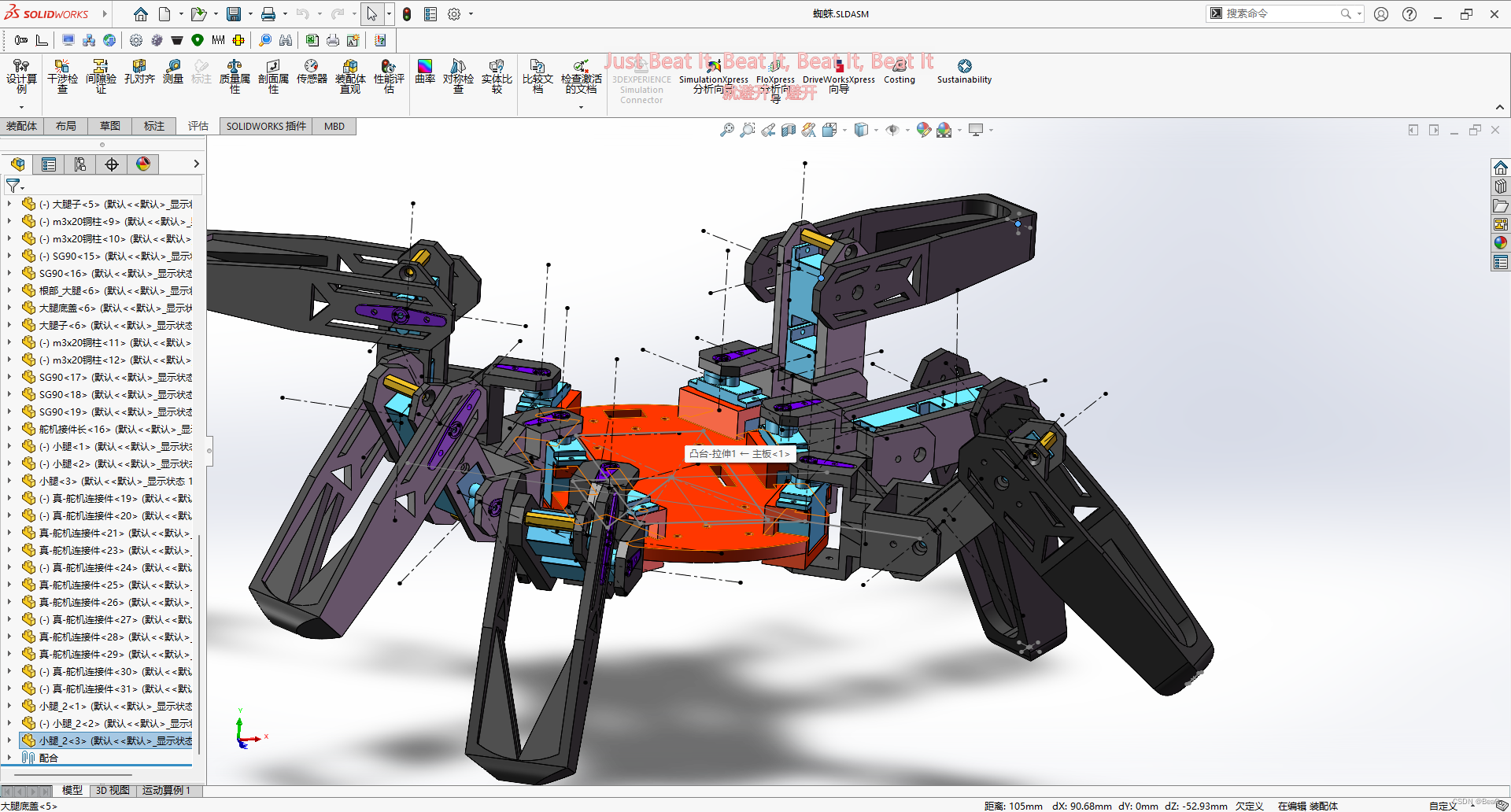








 本文作者分享了自学六足机器人过程中,如何从零开始掌握正运动学和逆运动学的求解。通过学习《机器人学导论》和MATLAB,实现了六足机器人一条腿的正逆运动学。详细介绍了DH参数的应用,正运动学的坐标计算,以及逆运动学的矩阵运算,最终得到了简单的逆解公式。整个过程充满挑战但也乐趣无穷,适合对机器人学感兴趣的读者参考。
本文作者分享了自学六足机器人过程中,如何从零开始掌握正运动学和逆运动学的求解。通过学习《机器人学导论》和MATLAB,实现了六足机器人一条腿的正逆运动学。详细介绍了DH参数的应用,正运动学的坐标计算,以及逆运动学的矩阵运算,最终得到了简单的逆解公式。整个过程充满挑战但也乐趣无穷,适合对机器人学感兴趣的读者参考。
















 1196
1196

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








