08.线性回归+从零实现+简洁实现(与课程对应)
目录
一、基础算法
1、线性回归
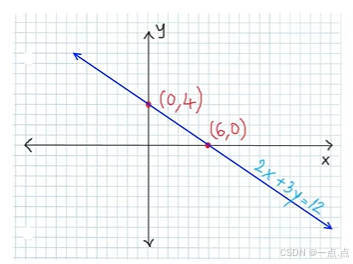
2、买房竞价应用:
- 买房流程:在美国买房需先看房了解信息,看中后参与竞价,给定时间窗内众多买家出价,价高者得房。
- 价格参考:卖房经纪人列价和 Redfin 网站估价仅供参考,最终成交价需买家自行出价竞争。
- 实例说明:以某房为例,列价 550 万美金,有 7 个卧室、5 个卫生间,居住面积 460 平米左右,Redfin 估价 540 万美金。
- 购房差价:展示两套房子成交价与系统估价情况,有买家因不懂规矩多花 10 万美金,系统估价在一年后仍低于其出价。
3、线性回归模型构建:
- 简化假设:假设影响房价的关键因素为卧室个数、卫生间个数和居住面积,分别记为 X1、X2、X3;成交价 y 是关键因素的加权和,即 y = W1*X1 + W2*X2 + W3*X3 + b ,其中权重 W1、W2、W3 和偏差 b 值后续确定。

- 一般化模型:给定 n 维输入 x(包含 x1 到 xn 项),线性模型有 n 维权重 w(含 w1 到 wn)和标量偏差 b,输出为输入的加权和加偏差,写成向量版本为输入 x 向量与权重 w 累积再加偏差 b。
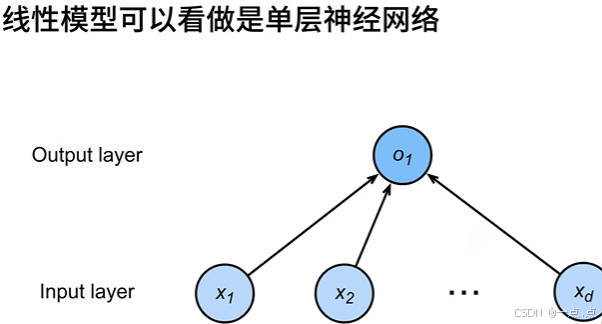
- 与神经网络关系:线性模型可看作单层神经网络,输入层有 n 个输入元素,输出层维度为 1,每箭头代表权重,此神经网络因带权重层仅一层而被称为单层神经系统,神经网络概念源于神经科学,虽现在发展超出其范畴,但部分模型仍有神经科学背景。
4、模型评估与参数学习:

- 损失函数定义:用平方损失衡量预测值y^与真实值y差异,即 1/2*(真实值 - 估计值)² ,其中 1/2 是为求导方便消去系数。
![]()
- 训练数据准备:基于数据学习模型参数,如采集过去 6 个月卖房信息及成交价作为训练数据,数据通常越多越好,但受多种因素限制,数据不足时有相关处理技术。
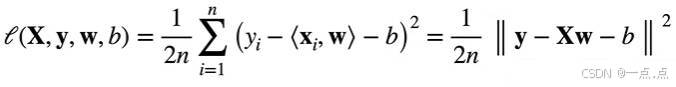
![]()
- 损失函数计算:假设有 n 个样本,将样本排列成矩阵形式,大 X 每行为一个样本,y 为列向量代表真实值,评估模型在每个数据上损失求均值得到损失函数,目标是找到使损失函数最小的权重 w 和偏差 b 。
二、从零实现
线性回归的从零实现(不使用任何的深度学习框架提供的计算,只使用最简单的在tensor上的计算):我们将从零开始实现整个方法,包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。
1、导入库
import random
import torch
from d2l import torch as d2l2、根据带有噪声的线性模型构造一个 人造数据集,我们使用线性模型参数 w = [2, -3.4]T、b = 4.2 和噪声项 ϵ,生成数据集及标签 y = Xw + b + ϵ
def synthetic_data(w, b, num_examples):
"""生成 y = Xw + b + 噪声"""
X = torch.normal(0, 1, (num_examples, len(w))) # 创建x,均值为0、方差为1的随机正态分布数,大小尺寸为(n个样本, w的长度)
y = torch.matmul(X, w) + b # y = Xw + b
y += torch.normal(0, 0.01, y.shape) # 加入随机噪音(均值为0,方差为0.01,形状与y相同):y = Xw + b + 噪声
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4]) # 真实的 w
true_b = 4.2 # 真实的 b
features, labels = synthetic_data(true_w, true_b, 1000) # 特征,标签
print("features:", features[0], "\nlabels:", labels[0]) # 打印第0个数据
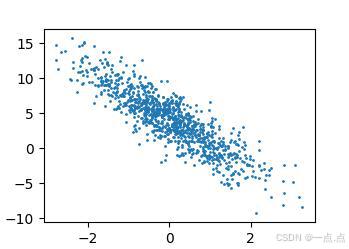
# 对样本数据集进行可视化
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
# d2l.plt.scatter(features[:, 1], labels, 1) # 这么写也行
d2l.plt.show() # 在线展示
3、每次读取小批量
def data_iter(batch_size, features, labels): # 批量大小,特征,标号
num_examples = len(features) # 样本数n
indices = list(range(num_examples)) # 0到n-1下标转成一个list
# 这些样本是随机读取的,没有特定的顺序
random.shuffle(indices) # 用random.shuffle()将下标完全打乱;这样就可以随机顺序去访问每个样本
for i in range(0, num_examples, batch_size): # 每一次从0开始,到n-1,每一次跳batch_size大小
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)]) # 前边没有到最后,那就取最小值;最后一次如果没有拿满会取个最小值
yield features[batch_indices], labels[batch_indices] # yield就是每次返回两组值,可以一直返回
batch_size = 10
# 打印一个批量的数据示例
for X, y in data_iter(batch_size, features, labels):
print('X:', X, '\n', 'y:', y)
break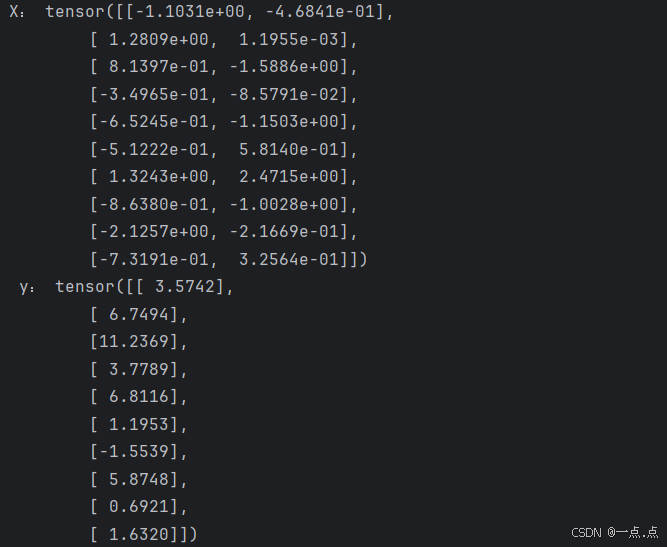
4、定义初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True) # 因为输入维度是2,所以w是一个长为2的向量,随机初始化为均值为0、方差为1 的随机的正太分布
b = torch.zeros(1, requires_grad=True) # 需要计算梯度
5、 定义模型
def linreg(X, w, b): # 给定输入X(就是批量大小);以及w, b
"""线性回归模型"""
return torch.matmul(X, w) + b # y = Xw + b6、 定义损失函数
def squqred_loss(y_hat, y): # y_hat预测值;y真实值
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape))**2 / 27、 定义优化算法
def sgd(params, lr, batch_size): # params所有参数,包含w、b;lr学习率;batch_size批量大小
"""小批量随机梯度下降"""
with torch.no_grad(): # 不需要计算梯度,更新的时候不要采用梯度计算
for param in params: # 对参数里面的每一个参数w、b
param -= lr * param.grad / batch_size # 自动求导时,导数存在.grad里面
param.grad.zero_() # 梯度设置为0,下一次计算梯度的时候,就不会跟上次的有关联了8、训练过程
# (1)超参数设置
lr = 0.03 # 学习率
num_epochs = 3 # 整个数据扫三遍
net = linreg # network 模型
loss = squqred_loss # 损失函数,均方损失
# (2)训练的实现大同小异,一般就是两层for循环:第一层是每一次对数据扫一遍;第二层是对于每一次拿出一个批量大小的X、y
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # 把 X, w, b 放到模型里面做预测;把 预测的y 与 真实的y 做损失;得到的损失就是 一个批量大小的向量
l.sum().backward() # 对loss求和(因为上一步得到的loss是批量大小的向量),求和之后算梯度
sgd([w, b], lr, batch_size) # 使用sgd()函数,来对w、b进行更新;此处的batch_size不够严谨,因为本次示例有100个样本,批量大小为10,所以可以整除,当遇到最后剩余的数据少于batch_size时,这么写会多出一部分,所以要进行特殊处理
# 对数据扫完一边之后,评价一下进度,此时是不需要梯度的,
with torch.no_grad():
train_l = loss(net(features, w, b), labels) # features, w, 传入到模型中,与真实的labels进行损失计算
print(f"epoch {epoch + 1}, loss {float(train_l.mean()):f}") # 打印评估的结果
9、 因为本次用的时人工数据集,可以看到真实的w、b;比较真实参数和通过训练学到的参数来评估训练的成功程度
print(f"w的估计误差:{true_w - w.reshape(true_w.shape)}")
print(f"b的估计误差:{true_b - b}")
10、完整代码:
import random
import torch
from d2l import torch as d2l
# 线性回归的从零实现(不使用任何的深度学习框架提供的计算,只使用最简单的在tensor上的计算):我们将从零开始实现整个方法,包括数据流水线、模型、损失函数和小批量随机梯度下降优化器
# 1、根据带有噪声的线性模型构造一个 人造数据集,我们使用线性模型参数 w = [2, -3.4]T、b = 4.2 和噪声项 ϵ,生成数据集及标签 y = Xw + b + ϵ
def synthetic_data(w, b, num_examples):
"""生成 y = Xw + b + 噪声"""
X = torch.normal(0, 1, (num_examples, len(w))) # 创建x,均值为0、方差为1的随机正态分布数,大小尺寸为(n个样本, w的长度)
y = torch.matmul(X, w) + b # y = Xw + b
y += torch.normal(0, 0.01, y.shape) # 加入随机噪音(均值为0,方差为0.01,形状与y相同):y = Xw + b + 噪声
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4]) # 真实的 w
true_b = 4.2 # 真实的 b
features, labels = synthetic_data(true_w, true_b, 1000) # 特征,标签
print("features:", features[0], "\nlabels:", labels[0]) # 打印第0个数据
# 对样本数据集进行可视化
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
# d2l.plt.scatter(features[:, 1], labels, 1) # 这么写也行
# d2l.plt.show() # 在线展示
# 2、每次读取小批量
def data_iter(batch_size, features, labels): # 批量大小,特征,标号
num_examples = len(features) # 样本数n
indices = list(range(num_examples)) # 0到n-1下标转成一个list
# 这些样本是随机读取的,没有特定的顺序
random.shuffle(indices) # 用random.shuffle()将下标完全打乱;这样就可以随机顺序去访问每个样本
for i in range(0, num_examples, batch_size): # 每一次从0开始,到n-1,每一次跳batch_size大小
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)]) # 前边没有到最后,那就取最小值;最后一次如果没有拿满会取个最小值
yield features[batch_indices], labels[batch_indices] # yield就是每次返回两组值,可以一直返回
batch_size = 10
# 打印一个批量的数据示例
for X, y in data_iter(batch_size, features, labels):
print(X, '\n', y)
break
# 3、定义初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True) # 因为输入维度是2,所以w是一个长为2的向量,随机初始化为均值为0、方差为1 的随机的正太分布
b = torch.zeros(1, requires_grad=True) # 需要计算梯度
# 4、定义模型
def linreg(X, w, b): # 给定输入X(就是批量大小);以及w, b
"""线性回归模型"""
return torch.matmul(X, w) + b # y = Xw + b
# 5、定义损失函数
def squqred_loss(y_hat, y): # y_hat预测值;y真实值
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape))**2 / 2
# 6、定义优化算法
def sgd(params, lr, batch_size): # params所有参数,包含w、b;lr学习率;batch_size批量大小
"""小批量随机梯度下降"""
with torch.no_grad(): # 不需要计算梯度,更新的时候不要采用梯度计算
for param in params: # 对参数里面的每一个参数w、b
param -= lr * param.grad / batch_size # 自动求导时,导数存在.grad里面
param.grad.zero_() # 梯度设置为0,下一次计算梯度的时候,就不会跟上次的有关联了
# 7、训练过程
# (1)超参数设置
lr = 0.03 # 学习率
num_epochs = 3 # 整个数据扫三遍
net = linreg # network 模型
loss = squqred_loss # 损失函数,均方损失
# (2)训练的实现大同小异,一般就是两层for循环:第一层是每一次对数据扫一遍;第二层是对于每一次拿出一个批量大小的X、y
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # 把 X, w, b 放到模型里面做预测;把 预测的y 与 真实的y 做损失;得到的损失就是 一个批量大小的向量
l.sum().backward() # 对loss求和(因为上一步得到的loss是批量大小的向量),求和之后算梯度
sgd([w, b], lr, batch_size) # 使用sgd()函数,来对w、b进行更新;此处的batch_size不够严谨,因为本次示例有100个样本,批量大小为10,所以可以整除,当遇到最后剩余的数据少于batch_size时,这么写会多出一部分,所以要进行特殊处理
# 对数据扫完一边之后,评价一下进度,此时是不需要梯度的,
with torch.no_grad():
train_l = loss(net(features, w, b), labels) # features, w, 传入到模型中,与真实的labels进行损失计算
print(f"epoch {epoch + 1}, loss {float(train_l.mean()):f}") # 打印评估的结果
# 8、因为本次用的时人工数据集,可以看到真实的w、b;比较真实参数和通过训练学到的参数来评估训练的成功程度
print(f"w的估计误差:{true_w - w.reshape(true_w.shape)}")
print(f"b的估计误差:{true_b - b}")
三、简洁实现
线性回归的简洁实现(使用深度学习框架提供的计算);包括数据流水线、模型、损失函数和小批量随机梯度下降优化器
1、导入库
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn
2、人造数据集,使用线性模型参数 w = [2, -3.4]T、b = 4.2;得到features, labels
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
def load_array(data_arrays, batch_size, is_train=True):
"""构造一个Pytorch数据迭代"""
dataset = data.TensorDataset(*data_arrays) # 得到数据集,*表示接受任意多个参数并将其放在一个元组中,拆包
return data.DataLoader(dataset, batch_size, shuffle=is_train) # 加载数据集,shuffle表示是否随机打乱
batch_size = 10
data_iter = load_array(data_arrays=(features, labels), batch_size=batch_size) # 把features, labels做成一个list传入到data.TensorDataset,得到数据集dataset
print(next(iter(data_iter)))
3、 模型定义;'nn'是神经网络的缩写
# (1)使用框架的预定义好的层
net = nn.Sequential(nn.Linear(2, 1)) # 指定输入维度为2,输出维度为1
# (2)初始化模型参数
net[0].weight.data.normal_(0, 0.01) # 就是对w初始化化为均值为0,方差为0.01的正态分布
net[0].bias.data.fill_(0) # 就是对b初始化为04、计算均方误差使用的是MSELoss类,也称为 平方范数
loss = nn.MSELoss()5、实例化SGD实例,优化器
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # 传入参数、学习率6、训练过程
# (1)超参数设置
num_epochs = 3 # 整个数据扫三遍
# (2)训练的实现大同小异,一般就是两层for循环:第一层是每一次对数据扫一遍;第二层是对于每一次拿出一个批量大小的X、y
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X), y) # 把 X 放到模型里面做预测(net本身自己带了模型参数,所以不需要w、b再传入了);把 预测的y 与 真实的y 做损失;得到的损失就是 一个批量大小的向量
trainer.zero_grad() # 优化器梯度清0
l.backward() # 求梯度,此处不用求sum,因为已经自动求完sum了
trainer.step() # 调用step()函数,进行一次模型参数的更新
# 对数据扫完一边之后,评价一下进度,此时是不需要梯度的,
l = loss(net(features), labels)
print(f"epoch {epoch + 1}, loss {l:f}") # 打印评估的结果
7、完整代码:
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn
# 线性回归的简洁实现(使用深度学习框架提供的计算);包括数据流水线、模型、损失函数和小批量随机梯度下降优化器
# 1、人造数据集,使用线性模型参数 w = [2, -3.4]T、b = 4.2;得到features, labels
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
def load_array(data_arrays, batch_size, is_train=True):
"""构造一个Pytorch数据迭代"""
dataset = data.TensorDataset(*data_arrays) # 得到数据集,*表示接受任意多个参数并将其放在一个元组中,拆包
return data.DataLoader(dataset, batch_size, shuffle=is_train) # 加载数据集,shuffle表示是否随机打乱
batch_size = 10
data_iter = load_array(data_arrays=(features, labels), batch_size=batch_size) # 把features, labels做成一个list传入到data.TensorDataset,得到数据集dataset
print(next(iter(data_iter)))
# 2、模型定义;'nn'是神经网络的缩写
# (1)使用框架的预定义好的层
net = nn.Sequential(nn.Linear(2, 1)) # 指定输入维度为2,输出维度为1
# (2)初始化模型参数
net[0].weight.data.normal_(0, 0.01) # 就是对w初始化化为均值为0,方差为0.01的正态分布
net[0].bias.data.fill_(0) # 就是对b初始化为0
# 3、计算均方误差使用的是MSELoss类,也称为 平方范数
loss = nn.MSELoss()
# 4、实例化SGD实例,优化器
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # 传入参数、学习率
# 5、训练过程
# (1)超参数设置
num_epochs = 3 # 整个数据扫三遍
# (2)训练的实现大同小异,一般就是两层for循环:第一层是每一次对数据扫一遍;第二层是对于每一次拿出一个批量大小的X、y
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X), y) # 把 X 放到模型里面做预测(net本身自己带了模型参数,所以不需要w、b再传入了);把 预测的y 与 真实的y 做损失;得到的损失就是 一个批量大小的向量
trainer.zero_grad() # 优化器梯度清0
l.backward() # 求梯度,此处不用求sum,因为已经自动求完sum了
trainer.step() # 调用step()函数,进行一次模型参数的更新
# 对数据扫完一边之后,评价一下进度,此时是不需要梯度的,
l = loss(net(features), labels)
print(f"epoch {epoch + 1}, loss {l:f}") # 打印评估的结果
如果此文章对您有所帮助,那就请点个赞吧,收藏+关注 那就更棒啦,十分感谢!!!
























 1667
1667

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








