向量代数
数量积
投影符号
向量积
方向性,由右手法则确定
几何应用,表示同时垂直于由a,b向量构成平面的法向量
混合积
几何应用,表示三个向量为棱边的平行六面体的体积
空间平面和直线
平面方程
(1)一般式:
(2)点法式:
注意点法式和一般式都直接给出了平面方程的法向量
(3)截距式:
(4)平面束:对于直线
可以给出平面束方程
在直线平面综合应用上非常实用
直线方程
(1)一般式,表示两个平面的交线
(2)对称式,对称式给出了直线的方向向量和经过的点
(3)由对称式可写出参数式
点面距离,点线距离
点面距离
点线距离,书上公式过于复杂,化简后易于理解
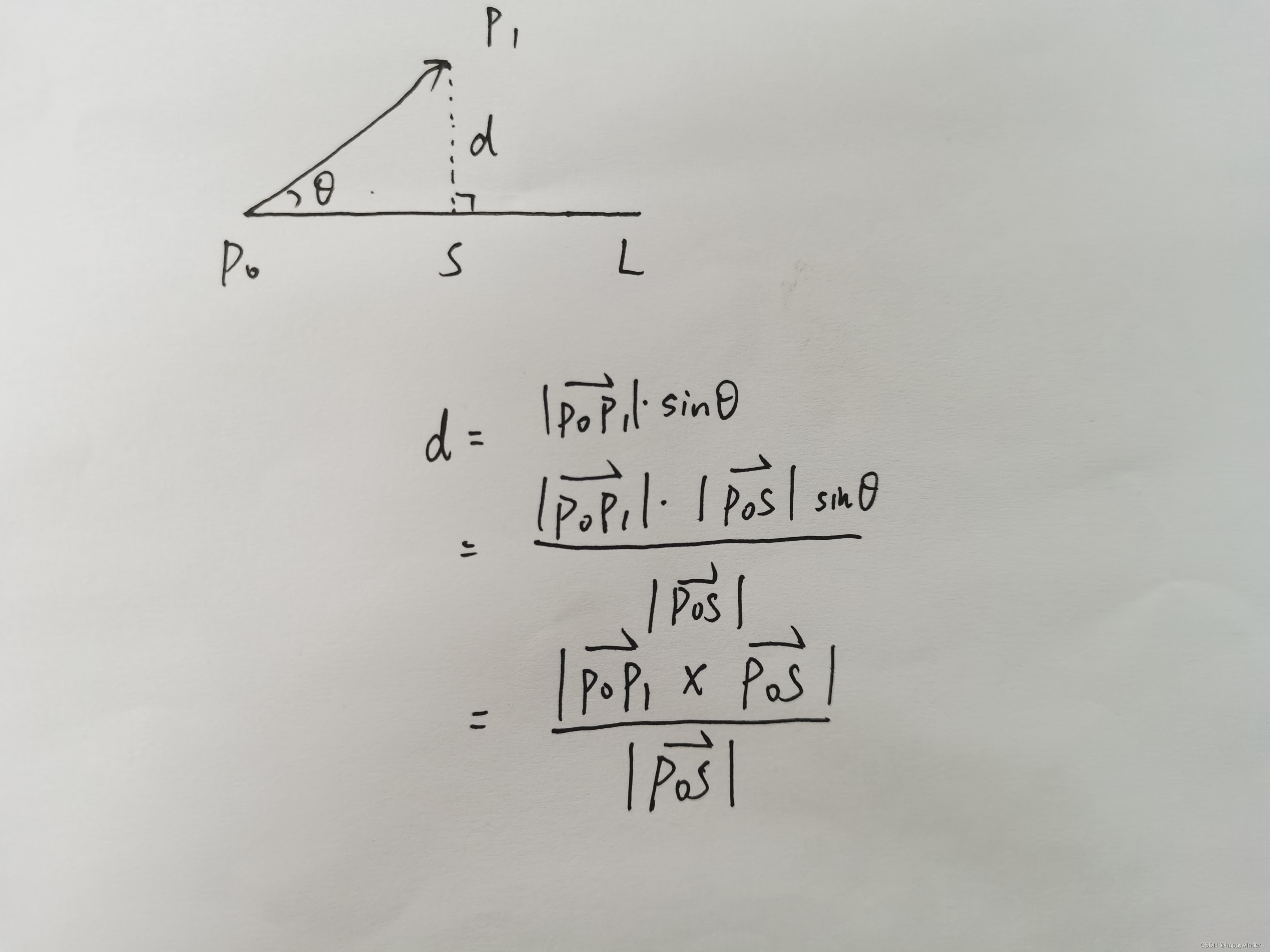








 本文介绍了向量代数的基础概念,包括数量积、向量积及其几何应用,如确定法向量和体积。同时,探讨了空间中平面的方程形式,如一般式、点法式和截距式,以及直线方程的不同表达方式。此外,还涉及点到面、点到线的距离计算方法。
本文介绍了向量代数的基础概念,包括数量积、向量积及其几何应用,如确定法向量和体积。同时,探讨了空间中平面的方程形式,如一般式、点法式和截距式,以及直线方程的不同表达方式。此外,还涉及点到面、点到线的距离计算方法。
















 504
504

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








