机器学习支持向量机SVM的原理、算法、应用解释及完整代码

1.引言
2.原理（线性可分、线性不可分、核函数）
3.时间序列SVM回归+贝叶斯寻找最优参数，可直接用

一.引言

1.支持向量机[1-2](support vector machines，SVM)是建立在统计学习理论[3-4]VC维理论和结构风险最小化原理基础上的机器学习方法。用于解决数据挖掘或模式 识别领域中数据分类问题它在解决小样本、非线性和高维模式识别问题中表现出许多特有的优势，并在很大程度上克服了“维数灾难”和“过学习”等问题。此外，它具有坚实的理论基础，简单明了的数学模型，因此，在模式识别、回归分析、函数估计、时间序列预测等领域都得到了长足的发展，并被广泛应用于文本识别[5]、手写字体识别[6]、人脸图像识别[7]、基因分类[8]及时间序列预测[9]等。

二、基本原理

它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。它基于结构风险最小化理论之上在特征空间中构建最优超平面，使得学习器得到全局最优化，并且在整个样本空间的期望以某个概率满足一定上界。
1.线性可分
首先，对于SVM来说，它用于二分类问题，也就是通过寻找一个分类线(二维是直线，三维是平面，多维是超平面）可以将数据分为两类。 并用线性函数f(x)=w*x+b来构造这个分类器(如下图是一个二维分类线）

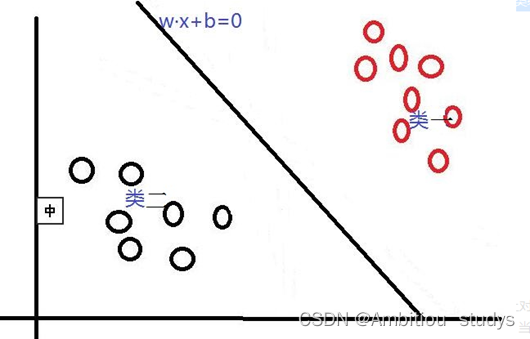
其中，w是权重向量，x为训练元组（X=(X1,X2…Xn),n为特征个数，Xi为每个X在属性i上对应的值），b为偏置，w•x是w和x的点积。当某数据被分类时，就会代入此函数，通过计算f(x)的值来确定所属的类别，当f(x)>0时，此数据被分为类一，当f(x)<0时，此数据被分为类二。通过观察，我们可以发现，如果我们平移或者旋转一下此分类线，同样可以完成数据的分类，那么，选择哪一个分类线才是最好的呢？

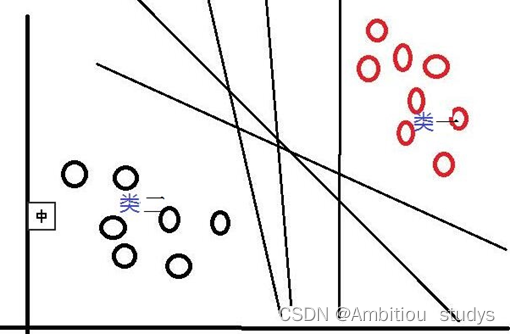
对于这个问题，SVM是通过搜索“最大边缘距离分类线”（面）来解决的。那么，什么是边缘距离，为什么要寻找最大的边缘距离呢？如下图所示，如果我们将某一分类线向右平移，在平移到右侧最大限度，又能确保此时的这个被平移的线仍然能将数据分为两类时，也就是如下图所示的：右侧与类一中某个或某些数据（实心点）相交的位置。此时正好，在线右侧和线上的数据是类一，在线左侧的数据是类二；同理，如果我们将这个分类线向左移动，也是移动到左侧最大限度（线二），此时这条线刚好也与类二中的某个或某些（实心点）数据相交，线上和线左侧的数据是类二，线右侧的数据是类一。对于这两条“极限边界线”，我们可以称之为支持线，或者对于面来说，就是支持面，而确定这些支持面或者支持线的那些数据点，我们称之为支持向量。两个支持线或支持面之间的这个距离，就是我们所说的边缘距离。

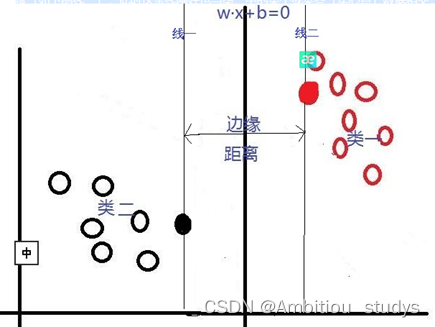
在这里我们可以发现，不同的分类线（面）会对应不同的支持线(面），支持线（面）之间的边缘距离也是不同的，并且，我们认为：边缘距离越大的分类线，对分类精度更有保证，所以，我们要找的”最好的“分类线（面），就是拥有最大边缘距离的那个分类线（面）。也就是说：对于线性可分的情况，SVM会选择最大化两类之间边缘距离的那个分类线（面）来完成二分类问题。并且此分类线（面）平行于两个支持线（面），平分边缘距离。下图是一个与上图相比，拥有更大边缘距离的分类线（面）。

2.线性不可分
对于线性可分的情况，我们上面说到，可以通过一个线性函数f(x)=w•x +b来构造一个分类器，寻找一个有着最大边缘距离的分类线（面）来完成对数据的分类。但是，我们还会遇到另一个问题，就是，如果数据是线性不可分的情况，用一个二维直线，三维平面或者多维超平面不能完成二分类，又该如何呢？对于线性不可分问题，SVM采取的方法是将这些线性不可分的原数据向高维空间转化，使其变得线性可分。就像下图所示，对于一些数据，他们是线性不可分的，那么，通过将他们向高维转化，也许就像图中所示，将二维数据转化到三维，就可以通过一个分类面将这些数据分为两类。所以说，SVM通过将线性不可分的数据映射到高维，使其能够线性可分，再应用线性可分情况的方法完成分类。而在这个高维转化过程中，SVM实际上并没有真正的进行高维映射，而是通过一种技巧来找出这个最大边缘分类面，即将一个叫做核函数的函数，应用于原输入数据上。
3.核函数
这个技巧首先允许我们不需要知道映射函数是什么，只将选定的核函数应用到原输入数据上就行；其次，所有的计算都在原来的低维输入数据空间进行，避免了高维运算。对于这个核函数，可选项有好几种，包括多项式核函数，高斯径向基函数核函数，S型核函数等

1.多项式核计算数据点之间的高维关系，并且在不添加任何特征的前提下将数据映射到更高的维度。这里的q是一个超参数，指的是函数应该使用的多项式的次数。
举个栗子，图一的数据是低维的线性不可分的，但是我们使用多项式核的SVM转化后，我们就得到了如图二所示的高维线性可分的映射。再说一遍，多项式内核只是把数据从低维映射到高维，并计算高维之间的关系，并不转化或者新增特征。另外，多项式次数越高，拟合能力越强，如果感觉模型过拟合了，可以适当减小多项式的次数。

2.高斯核也是拔高特征的维度，将低纬度的特征映射到高纬度，只不过映射方式使用的是高斯函数。其中，x表示样本点，x’表示地标。地标本质上是也是样本中的点，我们用来计算和其他样本点之间的相似性。如图三所示，是一个1维的图，图中有两个地标（红色的点），对于样本x=-1，它距离第一个地标1个距离，距离第二个地标 2个距离。

因此，将图三根据高斯公式被映射过后的特征如图四所示。我们可以很轻松的使用图中红线将样本点分为两类（蓝色和绿色）。

三、参考代码

1.时间序列SVM代码

# 1. 导入必要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from sklearn.svm import SVR  # 导入支持向量机回归模型
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import math  # 用于计算均方根误差（RMSE）

# 2. 加载数据
data1 = pd.read_csv(r'/data/train.csv')

# 筛选时间范围内的数据
start_time = '2020-06-01 '
end_time = '2024-12-31'
data = data1[(data1['date_time'] >= start_time) & (data1['date_time'] <= end_time)].copy()

# 确保日期时间列是 datetime 类型
data['date_time'] = pd.to_datetime(data['date_time'])

# 假设目标变量是 'car_obs'，特征变量是其他列（除了 'date_time' 和 'car_obs'）
target_column = 'car_obs'
features = [col for col in data.columns if col not in ['date_time', target_column]]

# 3. 数据预处理
# 将时间特征转换为数值特征（例如：小时、分钟等）
data['hour'] = data['date_time'].dt.hour
data['minute'] = data['date_time'].dt.minute

# 特征和目标变量
X = data[features + ['hour', 'minute']]
y = data[target_column]

# 数据标准化
scaler_X = StandardScaler()
scaler_y = StandardScaler()

X_scaled = scaler_X.fit_transform(X)
y_scaled = scaler_y.fit_transform(y.values.reshape(-1, 1)).flatten()

# 数据集划分（75% 训练集，25% 测试集）
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.25, random_state=42)

# 4. 使用支持向量机（SVM）进行建模
svm_model = SVR(kernel='rbf', C=1.0, epsilon=0.1)  # 使用 RBF 核
svm_model.fit(X_train, y_train)

# 5. 预测
y_pred_train_scaled = svm_model.predict(X_train)  # 训练集预测
y_pred_test_scaled = svm_model.predict(X_test)    # 测试集预测

# 反标准化预测结果和真实值
y_pred_train = scaler_y.inverse_transform(y_pred_train_scaled.reshape(-1, 1)).flatten()
y_pred_test = scaler_y.inverse_transform(y_pred_test_scaled.reshape(-1, 1)).flatten()
y_train = scaler_y.inverse_transform(y_train.reshape(-1, 1)).flatten()
y_test = scaler_y.inverse_transform(y_test.reshape(-1, 1)).flatten()

# 6. 模型评估
# 测试集评估指标
mse_test = mean_squared_error(y_test, y_pred_test)
rmse_test = math.sqrt(mse_test)
mae_test = mean_absolute_error(y_test, y_pred_test)
r2_test = r2_score(y_test, y_pred_test)
mbe_test = np.mean(y_pred_test - y_test)  # 均方偏差（MBE）

# 训练集评估指标
mse_train = mean_squared_error(y_train, y_pred_train)
rmse_train = math.sqrt(mse_train)
mae_train = mean_absolute_error(y_train, y_pred_train)
r2_train = r2_score(y_train, y_pred_train)
mbe_train = np.mean(y_pred_train - y_train)  # 均方偏差（MBE）

# 打印测试集评估指标
print("测试集评估指标：")
print(f"均方误差 (MSE): {mse_test:.4f}")
print(f"均方根误差 (RMSE): {rmse_test:.4f}")
print(f"平均绝对误差 (MAE): {mae_test:.4f}")
print(f"决定系数 (R²): {r2_test:.4f}")
print(f"均方偏差 (MBE): {mbe_test:.4f}")

# 打印训练集评估指标
print("\n训练集评估指标：")
print(f"均方误差 (MSE): {mse_train:.4f}")
print(f"均方根误差 (RMSE): {rmse_train:.4f}")
print(f"平均绝对误差 (MAE): {mae_train:.4f}")
print(f"决定系数 (R²): {r2_train:.4f}")
print(f"均方偏差 (MBE): {mbe_train:.4f}")

# 7. 可视化预测结果
# 测试集可视化
plt.figure(figsize=(12, 6))
plt.plot(y_test, label='True Values (Test)', color='blue')
plt.plot(y_pred_test, label='Predicted Values (Test)', color='red', linestyle='--')
plt.xlabel('Sample Index')
plt.ylabel('car ')
plt.title('SVM car  Prediction (Test Set)')
plt.legend()
plt.show()

# 训练集可视化
plt.figure(figsize=(12, 6))
plt.plot(y_train, label='True Values (Train)', color='blue')
plt.plot(y_pred_train, label='Predicted Values (Train)', color='green', linestyle='--')
plt.xlabel('Sample Index')
plt.ylabel('car')
plt.title('SVM car Prediction (Train Set)')
plt.legend()
plt.show()

2.使用 GridSearchCV 或 RandomizedSearchCV 来优化支持向量回归（SVR）模型的超参数

# 1. 导入必要的库
from sklearn.model_selection import t GridSearchCV


# 4. 使用 GridSearchCV 寻找最优参数
param_grid = {
    'C': [0.1, 1, 10, 100],  # 惩罚参数
    'epsilon': [0.01, 0.1, 0.2, 0.5],  # 误差容忍度
    'gamma': [1e-3, 1e-2, 1e-1, 1],  # RBF核的参数
    'kernel': ['linear', 'poly', 'rbf', 'sigmoid'],  # 核函数类型
    'degree': [2, 3, 4, 5],  # 多项式核的阶数
    'coef0': [0, 0.5, 1],  # 核函数的常数项
    'tol': [1e-5, 1e-4, 1e-3, 1e-2],  # 收敛容差
    'shrinking': [True, False],  # 是否使用收缩启发式
    'max_iter': [-1, 1000, 5000, 10000]  # 最大迭代次数
}
svr = SVR(kernel='rbf')
grid_search = GridSearchCV(estimator=svr, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1, verbose=1)
grid_search.fit(X_train, y_train)

# 输出最优参数
print("Best parameters found: ", grid_search.best_params_)
print("Best cross-validation score: ", -grid_search.best_score_)

# 使用最优参数重新训练模型
best_svr = grid_search.best_estimator_

# 5. 预测
y_pred_train_scaled = best_svr.predict(X_train)
y_pred_test_scaled = best_svr.predict(X_test)

# 反标准化预测结果和真实值
y_pred_train = scaler_y.inverse_transform(y_pred_train_scaled.reshape(-1, 1)).flatten()
y_pred_test = scaler_y.inverse_transform(y_pred_test_scaled.reshape(-1, 1)).flatten()
y_train = scaler_y.inverse_transform(y_train.reshape(-1, 1)).flatten()
y_test = scaler_y.inverse_transform(y_test.reshape(-1, 1)).flatten()

# 6. 模型评估
mse_test = mean_squared_error(y_test, y_pred_test)
rmse_test = math.sqrt(mse_test)
mae_test = mean_absolute_error(y_test, y_pred_test)
r2_test = r2_score(y_test, y_pred_test)
mbe_test = np.mean(y_pred_test - y_test)

mse_train = mean_squared_error(y_train, y_pred_train)
rmse_train = math.sqrt(mse_train)
mae_train = mean_absolute_error(y_train, y_pred_train)
r2_train = r2_score(y_train, y_pred_train)
mbe_train = np.mean(y_pred_train - y_train)

print("\n测试集评估指标：")
print(f"均方误差 (MSE): {mse_test:.4f}")
print(f"均方根误差 (RMSE): {rmse_test:.4f}")
print(f"平均绝对误差 (MAE): {mae_test:.4f}")
print(f"决定系数 (R²): {r2_test:.4f}")
print(f"均方偏差 (MBE): {mbe_test:.4f}")

print("\n训练集评估指标：")
print(f"均方误差 (MSE): {mse_train:.4f}")
print(f"均方根误差 (RMSE): {rmse_train:.4f}")
print(f"平均绝对误差 (MAE): {mae_train:.4f}")
print(f"决定系数 (R²): {r2_train:.4f}")
print(f"均方偏差 (MBE): {mbe_train:.4f}")