练习放在文末
同态映射

这里算是重点(老师在这里讲了很长时间,而且这里比较抽象)

找到的一个比较好的解释
同态像

同态象 <f(S),∗′,Δ′,k′> ,是代数系统 A′=<S′,∗′,Δ′,k′> 的子代数(该条是一个定理,下面会有证明)
我的理解就是A的元素通过 f 关系变成 f(A),然后f(A)是已经映射到B上的了,那么f(A)应该是与B中的运算符相关的,所以是<f(S),∗′,Δ′,k′>。而象的概念在之前二元关系这一章有(A的象是ran(F限制A)),所以同态象的定义即是<f(S),∗′,Δ′,k′>是V1的同态象
说明


同态映射的分类
同构就是f是双射
实例

性质

同余关系与同余类

a~b——f(a)=f(b)
运算上的同余关系:
设A=<S,*,Δ>是一个代数系统,~是载体S上的等价关系,任取a,b,c∈S。
(1)当a~b时,若Δa~Δb,则等价关系~在一元运算Δ下是可保持的,称~是关于运算Δ的同余关系。
(2)当a~b和c~d时,若有a*c~b*d,则等价关系~在二元运算*下是可保持的,称~是关于运算*的同余关系。
等价关系在运算下的可保持性是指参与运算的对应元素,如果在同一个等价类中,则运算后所得的结果也必在同一个等价类中
代数系统上的同余关系:
设A=<S,*,Δ>是一个代数系统,~是载体S上的等价关系,若~在A上的所有运算下都是可保持的,则称~为代数系统A上的同余关系。 同余关系使得元素所在的等价类在运算上可以作为一个整体来看待
设g是从代数系统A=<S,*,Δ,k>到A’=<S’,*’,Δ’,k’>的一个同态映射,如果在A上定义等价关系R为:<a,b>∈R,当且仅当g(a)=g(b),则R是A上的一个同余关系。
证明:
(i)若a~b,则g(a)=g(b),Δ’g(a)=Δ’g(b)。又g是从A到A’的同态映射,所以有Δ’g(a)=g(Δa)=Δ’g(b)=g(Δb) 故Δa~Δb,这说明~在运算Δ下是可保持的。
(ii)若a~b且c~d,且有g(a)=g(b),g(c)=g(d),所以 g(a)*’g(c)=g(b)*’g(d),又因g是从A到A’的同态映射,所以有g(a)*’g(c)=g(a*c)=g(b)*’g(d)=g(b*d),故a*c~b*d,这说明等价关系~在运算*下是可保持的。
由(i)(ii)可得,~是代数系统A上的同余关系

商代数

例子

性质

不一定满足消去律




例题
先找自同态


要证明R是f导出的同余关系,需要证明——当有a~b,f(a)~f(b)
这个(4)的原理是 任何商代数都是同态像 ,所以证明同态像为V1,然后知道f导出的R,就知道(V1*V2)/R和V1同构
练习
11题

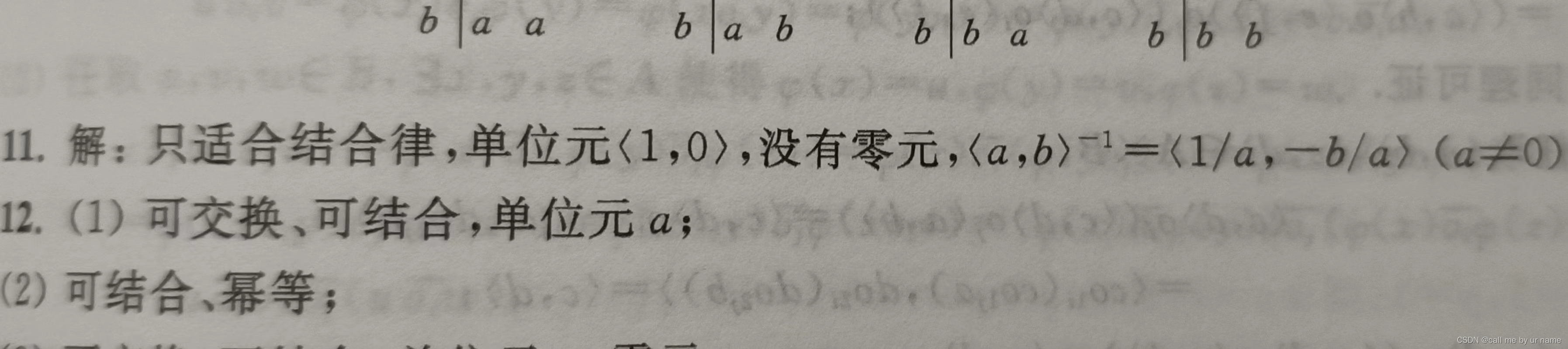 这道题的解法应该不是很规范,看看就行
这道题的解法应该不是很规范,看看就行
14题
这道题没难度
16题


没有难度
20题
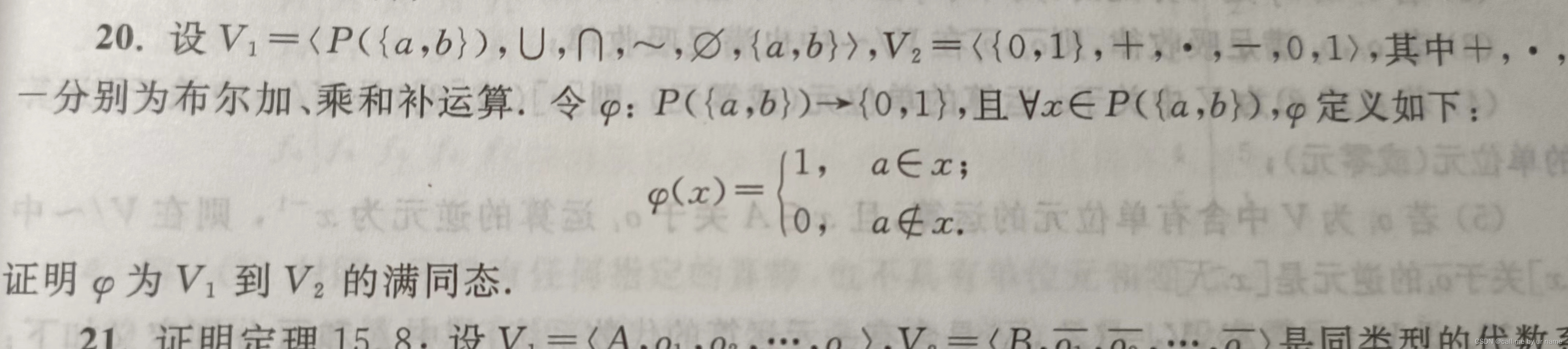
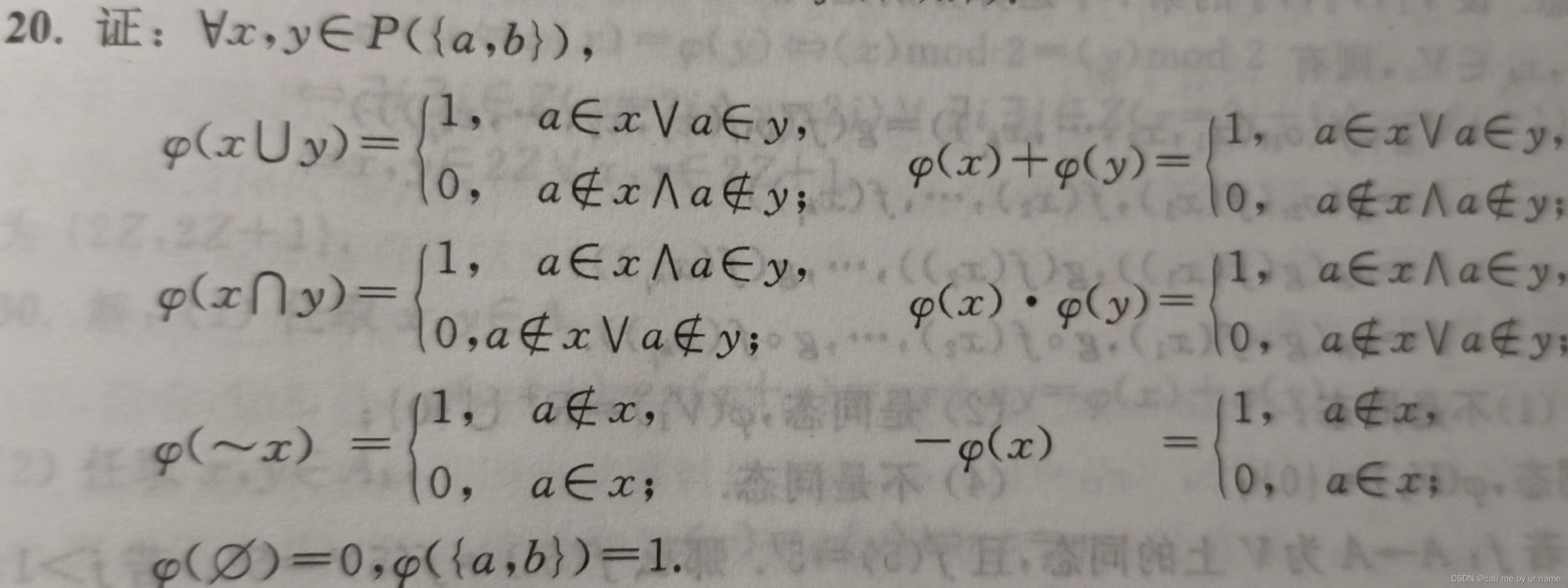
首先,证明同态映射(也要满足代数常元);接着,易知满射
之前,写得不太好
要证明满同态,应该是像题目中这样,同态映射的基础上(而且取值那里也要两边也要一致),然后f(x)知道满射
看看怎么证明同态映射,对应好相应的运算符,然后,进行同态映射
24题


这个题做法就是看——f(x*x)=x*x(受条件限制,无法展示得很贴切,但是应该能看懂我的意思)
(3)属于零同态,但(4)不是同态
29题
好好看(1),当然也不一定非要这么做,证明右边等于左边也可以。重要的是清楚证明同态的过程
第2问主要是通过商集导出划分,而商集需要等价关系,而等价关系可以通过同余关系得知(mod2易知满足同余关系),之后的步骤就很清晰了
30题


看看第(2)问,确定商代数
1.看n是否为0
2.确定商代数的运算符,关于这个,如果给出了具体的元素时,自设一个运算符,然后用运算表;但是像这道题这样的












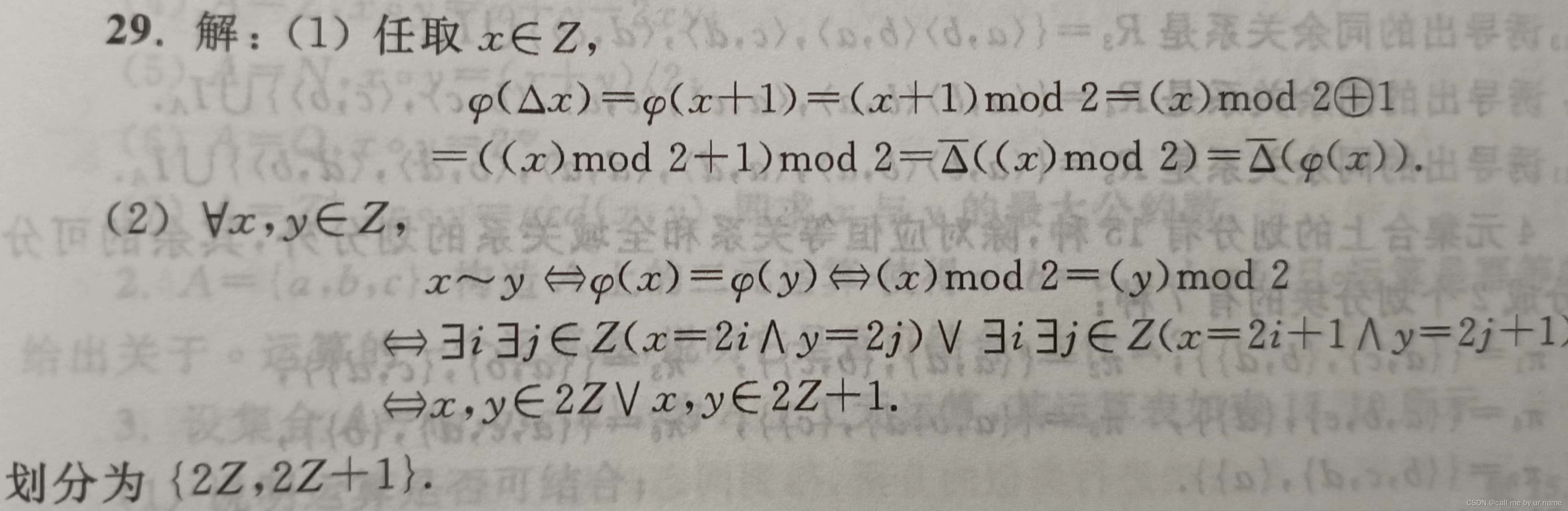
















 4289
4289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








