时间序列预测的迁移学习

在本文中，我们将了解如何将迁移学习应用于时间序列预测，以及如何在多样化的时间序列数据集上训练一次预测模型，之后无需训练即可在不同数据集上进行预测。我们将使用开源 Darts 库，仅用几行代码即可完成所有这些操作。你可以点击此处一个包含复现结果所需所有内容的独立笔记本。

---

时间序列预测在供应链、能源、农业、控制、IT 运营、金融等领域应用广泛。长期以来，表现最优的方法是指数平滑法或 ARIMA 等相对复杂的统计方法。但近年来，机器学习和深度学习在许多预测任务与竞赛中开始超越这些经典方法。

机器学习模型的显著特点在于，其参数可在大量序列上进行估算，这与传统方法通常一次仅估算一个序列不同。尽管机器学习潜力巨大，但其应用仍面临实际挑战：一方面，需要足够数据训练，这在某些场景下会引发冷启动问题，即数据不足时模型难以有效工作；另一方面，即便数据充足，模型训练也更复杂 —— 虽然借助 Darts 等工具可简化训练代码，但训练大型模型仍需耗时的超参数调优、特定硬件（如 GPU），或对数据与模型管理的基础设施及流程进行调整。

在本文中，我将探讨迁移学习在时间序列预测中的应用。我会在一个庞大且多样的时间序列数据集上训练深度学习模型，并观察其预测不同数据集里各类时间序列的表现。这一过程本身就颇具价值，因为它意味着来自人口统计、金融、工业等不同领域的时间序列可能共享某些共同特征。从元学习（或 “学习如何学习”）角度看，这也符合对 “学习任务” 的定义 —— 模型可在推理时适应新任务（如预测新时间序列），而无需重新训练。

除易用性外，在需最小化推理时间的场景中，使用无需训练的模型优势显著。以神经网络为例，其推理时间通常很短，仅需前向传播。在本文中，我将训练一个大型模型，它仅需几毫秒即可完成对未知新时间序列的预测。

我将使用 Darts 开源 Python 时间序列库，仅用几行代码就能完成模型训练与使用。Darts 功能丰富，可用于训练多变量序列（每个时间序列包含多个维度）模型、提供概率预测，还能纳入外部数据（协变量）。本文中，我仅用其对大量单变量时间序列进行预测。我会在文中提供关键代码片段，并 在此处 附上用于复现结果的完整笔记本（含所需数据集下载方式）。

航班乘客(Air Passengers)

让我们首先加载包含不同航空公司乘客数量的数据集：

air_train, air_test = load_air()

这里虽未展示 load_air () 函数，但它会返回两个列表，每个列表包含 301 个月度 TimeSeries 对象。其中，air_train 列表包含序列的训练部分（平均长度约为 137 个月），air_test 列表则包含最近 18 个月的数据，我将其作为验证集。（注意：一个好的做法是再留出一个测试集，在最终模型选定之前不触碰它）。

我在此使用 18 个月的预测范围，这与 M3 和 M4 竞赛中用于月度序列的范围一致（我会在本文后面使用它们的数据集）。此外，我将采用对称平均绝对百分比误差（sMAPE）作为误差指标，评估预测质量。

下面，我来绘制一些训练序列：

这是构成我们训练数据集的几个航空运输序列（不同航空公司）。大多数序列看起来差异很大，甚至没有相同的时间轴。例如，某些序列从 2001 年 1 月开始，而另一些则从 2010 年 4 月开始。你可以看到，这些训练序列的最大值均为 1—— 我使用了 Darts 缩放器（封装了 scikit-learn 的 MaxAbsScaler），将每个序列除以其最大绝对值。这种缩放不会影响对称平均绝对百分比误差（sMAPE），因此为了简化，这里仅处理缩放后的序列。在实际应用中，我需要对预测结果调用 scaler.inverse_transform ()，将其转换回原始值域。

用局部模型预测航空旅客量

现在，我尝试用 “经典” 方法为 300 个时间序列各拟合一个模型进行预测。我们将这种在单个序列上训练的模型称为局部模型。下面，我先编写两个小函数，以便后续使用。首先，eval_forecasts () 计算所有测试序列（300 个）预测误差的中位数 sMAPE，并展示误差分布。

def eval_forecasts(
    pred_series: List[TimeSeries], test_series: List[TimeSeries]
) -> List[float]:

    print("computing sMAPEs...")
    smapes = smape(test_series, pred_series)
    plt.figure()
    plt.hist(smapes, bins=50)
    plt.ylabel("Count")
    plt.xlabel("sMAPE")
    plt.title("Median sMAPE: %.3f" % np.median(smapes))
    plt.show()
    plt.close()
    return smapes

其次，eval_local_model()迭代所有序列，并为每个序列构建一个（本地）模型，将其拟合到序列的训练部分，并存储预测结果。然后调用此函数eval_forecasts()显示所有序列的 sMAPE 误差。函数返回所有误差的列表以及总耗时。

def eval_local_model(
    train_series: List[TimeSeries], test_series: List[TimeSeries], model_cls, **kwargs
) -> Tuple[List[float], float]:
    preds = []
    start_time = time.time()
    for series in tqdm(train_series):
        model = model_cls(**kwargs)
        model.fit(series)
        pred = model.predict(n=HORIZON)
        preds.append(pred)
    elapsed_time = time.time() - start_time

    smapes = eval_forecasts(preds, test_series)
    return smapes, elapsed_time

获取一些预测

现在我们可以在这个数据集上尝试第一个预测模型。作为第一步，通常最好先看看一个（非常）简单的模型（盲目地重复训练序列的最后一个值）的表现如何。这可以在 Darts 中使用NaiveSeasonal模型来实现：

naive1_smapes, naive1_time = eval_local_model(air_train, air_test, NaiveSeasonal, K=1)

因此，最朴素的模型得出的中值 sMAPE 约为 29.4。我们能否利用大多数月度序列的季节性为 12 这一事实，用一个“不那么朴素”的模型来做得更好？ 

naive12_smapes, naive12_time = eval_local_model(
    air_train, air_test, NaiveSeasonal, K=12
)

这样就好多了。我们来试试指数平滑（ExponentialSmoothing）（默认情况下，对于月度序列，它将使用季节性 12）。 

ets_smapes, ets_time = eval_local_model(air_train, air_test, ExponentialSmoothing)

看的出来效果真的是太棒了！现在我希望读者们能明白这有多简单。我们再尝试几个模型： 

theta_smapes, theta_time = eval_local_model(air_train, air_test, Theta, theta=1.5)

arima_smapes, arima_time = eval_local_model(air_train, air_test, ARIMA, p=12, d=1, q=1)

对比可以看出，ARIMA 胜出。让我们绘制每个模型获得的（中位数）误差与拟合和预测所需时间的关系图： 

ARIMA 的结果最好，但它也是（迄今为止）最耗时的模型。Theta 方法提供了一个有趣的权衡，它具有良好的预测精度，并且比 ARIMA 快大约 50 倍。我们能否通过考虑全局模型（即只对所有时间序列进行一次联合训练的模型）来找到更好的折衷方案？ 

利用全球模型预测航空旅客数量

在本节中，我们将使用“全局模型”——即同时在多个序列上进行训练的模型。Darts 本质上有两种全局模型：

• RegressionModels它们是类似 sklearn 的回归模型的包装器。
• 基于 PyTorch 的模型，提供各种深度学习模型。

这两种模型都可以通过“表格化”数据在多个系列上进行训练——即从所有训练系列中获取许多（输入、输出）子切片，并以监督的方式训练机器学习模型，根据输入预测输出。

我们首先定义一个eval_global_model()与 类似eval_local_model()但针对全局模型的函数。

def eval_global_model(
    train_series: List[TimeSeries], test_series: List[TimeSeries], model_cls, **kwargs
) -> Tuple[List[float], float]:

    start_time = time.time()

    model = model_cls(**kwargs)
    model.fit(train_series)
    preds = model.predict(n=HORIZON, series=train_series)

    elapsed_time = time.time() - start_time

    smapes = eval_forecasts(preds, test_series)
    return smapes, elapsed_time

使用RegressionModel​

Darts 中的预测模型可以与任何“兼容 scikit-learn”的回归模型结合使用，从而获得预测结果。与深度学习相比，它们代表了良好的全局模型，因为它们通常没有太多超参数，并且训练速度更快。此外，Darts 还提供了一些预打包的回归模型，例如LinearRegressionModel和LightGBMModel。

我们现在将使用我们的函数eval_global_models()并尝试一些回归模型。

读者们可以参考API 文档了解如何使用这些模型。重要的参数是lags和output_chunk_length。它们分别决定了模型使用的回溯窗口和“前瞻窗口”的长度，并且对应于用于训练的输入/输出子切片的长度。例如lags=24， 和output_chunk_length=12表示模型将使用过去的 24 个滞后值来预测接下来的 12 个滞后值。在我们的例子中，由于最短的训练序列长度为 36，因此 必须为lags + output_chunk_length <= 36。（请注意，lags也可以是一个整数列表，表示模型将使用的各个滞后值，而不是窗口长度）。

让我们尝试一下线性回归：

lr_smapes, lr_time = eval_global_model(
    air_train, air_test, LinearRegressionModel, lags=30, output_chunk_length=1
)

LGBM:

lgbm_smapes, lgbm_time = eval_global_model(
    air_train, air_test, LightGBMModel, lags=35, output_chunk_length=1, objective="mape"
)

随机森林： 

rf_smapes, rf_time = eval_global_model(
    air_train, air_test, RandomForest, lags=30, output_chunk_length=1
)

使用深度学习

接下来，我们将在数据集上训练一个 N-BEATS 模型air。同样，读者可以参考API 文档获取超参数的文档。以下超参数应该是一个很好的起点：

# Slicing hyper-params:
IN_LEN = 30
OUT_LEN = 4

# Architecture hyper-params:
NUM_STACKS = 20
NUM_BLOCKS = 1
NUM_LAYERS = 2
LAYER_WIDTH = 136
COEFFS_DIM = 11

# Training settings:
LR = 1e-3
BATCH_SIZE = 1024
MAX_SAMPLES_PER_TS = 10
NUM_EPOCHS = 10

现在让我们构建模型，进行训练，并得到一些预测结果。在（速度较慢的）Colab GPU 上，训练大约需要一两分钟。

# reproducibility
np.random.seed(42)
torch.manual_seed(42)

start_time = time.time()

nbeats_model_air = NBEATSModel(
    input_chunk_length=IN_LEN,
    output_chunk_length=OUT_LEN,
    num_stacks=NUM_STACKS,
    num_blocks=NUM_BLOCKS,
    num_layers=NUM_LAYERS,
    layer_widths=LAYER_WIDTH,
    expansion_coefficient_dim=COEFFS_DIM,
    loss_fn=SmapeLoss(),
    batch_size=BATCH_SIZE,
    optimizer_kwargs={"lr": LR},
    # remove this one if your notebook does run in a GPU environment:
    pl_trainer_kwargs={
        "enable_progress_bar": True,
        "accelerator": "gpu",
        "gpus": -1,
        "auto_select_gpus": True,
    },
)

nbeats_model_air.fit(
    air_train, num_loader_workers=4, epochs=NUM_EPOCHS
)

# get predictions
nb_preds = nbeats_model_air.predict(series=air_train, n=HORIZON)
nbeats_elapsed_time = time.time() - start_time

nbeats_smapes = eval_forecasts(nb_preds, air_test)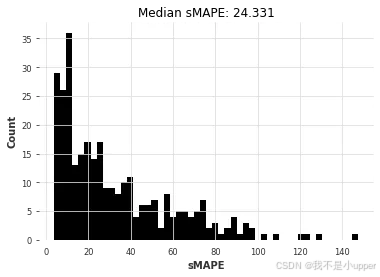

让我们再次比较一下我们的模型： 

 

 

因此，看起来，对所有序列进行联合训练的线性回归模型现在在准确率和速度之间实现了最佳平衡（在相似准确率的情况下，比 ARIMA 快约 85 倍）。线性回归通常是最佳选择！

我们的深度学习模型 N-BEATS 表现不佳。需要注意的是，我们尚未尝试针对这个问题进行明确的调优，这或许能带来更准确的结果。与其花时间进行调优，不如在下一节中，看看在完全不同的数据集上训练它是否能取得更好的效果。

使用 N-BEATS 模型进行迁移学习

深度学习模型通常在大型数据集上训练时表现更佳。让我们尝试加载 M4 竞赛数据集中全部 48,000 个月度时间序列，并在这个更大的数据集上再次训练我们的模型。

m4_train, _ = load_m4()

我们现在将再次尝试训练 N-BEATS 模型，但使用这个更大的数据集。

默认情况下，从给定序列中训练基于 ML 的预测模型所生成的（输入、输出）训练样本的数量与序列数量乘以其长度成正比。M4 数据集包含 48,000 个序列，平均长度约为 216 个时间步长。因此，如果我们保留默认参数，最终将得到约 10M 个数量级的训练样本。为了在一定程度上限制每个时期所需的时间，我们将限制每个序列使用的训练样本数量。这是在fit()使用参数调用时完成的max_samples_per_ts。我们添加了一个新的超参数MAX_SAMPLES_PER_TS来捕获它。注意：如果我们想要更好地控制生成（输入、输出）训练示例以训练模型的方式，我们可以调用fit_from_dataset()而不是fit()并提供darts.utils.data.TrainingDataset我们选择的实现。

由于 M4 训练系列都稍长一些，我们也可以使用稍长一些的input_chunk_length。

# Slicing hyper-params:
IN_LEN = 36
OUT_LEN = 4

# Architecture hyper-params:
NUM_STACKS = 20
NUM_BLOCKS = 1
NUM_LAYERS = 2
LAYER_WIDTH = 136
COEFFS_DIM = 11

# Training settings:
LR = 1e-3
BATCH_SIZE = 1024
MAX_SAMPLES_PER_TS = (
    10  # <-- new parameter, limiting the number of training samples per series
)
NUM_EPOCHS = 5

现在我们可以再次构建和训练我们的模型：

# reproducibility
np.random.seed(42)
torch.manual_seed(42)

nbeats_model_m4 = NBEATSModel(
    input_chunk_length=IN_LEN,
    output_chunk_length=OUT_LEN,
    batch_size=BATCH_SIZE,
    num_stacks=NUM_STACKS,
    num_blocks=NUM_BLOCKS,
    num_layers=NUM_LAYERS,
    layer_widths=LAYER_WIDTH,
    expansion_coefficient_dim=COEFFS_DIM,
    loss_fn=SmapeLoss(),
    optimizer_kwargs={"lr": LR},
    pl_trainer_kwargs={
        "enable_progress_bar": True,
        "accelerator": "gpu",
        "gpus": -1,
        "auto_select_gpus": True,
    },
)

# Train
nbeats_model_m4.fit(
    m4_train,
    num_loader_workers=4,
    epochs=NUM_EPOCHS,
    max_samples_per_ts=MAX_SAMPLES_PER_TS,
)

我们现在可以使用 M4 训练的模型来预测航空旅客序列。由于我们在这里以迁移学习的方式使用该模型，因此我们只计算推理部分（假设该模型已预先训练过）。 

start_time = time.time()
preds = nbeats_model_m4.predict(series=air_train, n=HORIZON)  # get forecasts
nbeats_m4_elapsed_time = time.time() - start_time
nbeats_m4_smapes = eval_forecasts(preds, air_test)

让我们再次比较一下所有模型： 

虽然准确率并非绝对最佳，但我们在 M4 上预训练的 N-BEATS 模型达到了相当高的准确率。这非常了不起，因为该模型从未在我们要求其预测的任何航空旅客序列上进行过训练！使用 N-BEATS 的预测步骤比我们使用 ARIMA 所需的拟合预测步骤快约 350 倍，比线性回归的拟合预测步骤快约 4 倍。为了好玩，我们还可以手动检查该模型在其他系列上的表现——例如，每月牛奶产量系列darts.datasets：

from darts.datasets import MonthlyMilkDataset

series = MonthlyMilkDataset().load().astype(np.float32)
train, val = series[:-24], series[-24:]

scaler = Scaler(scaler=MaxAbsScaler())
train = scaler.fit_transform(train)
val = scaler.transform(val)
series = scaler.transform(series)
pred = nbeats_model_m4.predict(series=train, n=24)

series.plot(label="actual")
pred.plot(label="0-shot forecast")

看来这个模型在月度序列上表现相当出色。这是 N-BEATS 的特性吗？或者如果我们在 M4 上训练其他全局模型（例如线性回归或 LGBM），然后在航空旅客序列上进行评估，会不会得到类似的结果？

尝试将迁移学习与其他全局模型结合

我们先尝试一下LinearRegressionModel

lr_model_m4 = LinearRegressionModel(lags=30, output_chunk_length=1)
lr_model_m4.fit(m4_train)

tic = time.time()
preds = lr_model_m4.predict(n=HORIZON, series=air_train)
lr_time_transfer = time.time() - tic

lr_smapes_transfer = eval_forecasts(preds, air_test)

 

再加上LightGBMModel

lgbm_model_m4 = LightGBMModel(lags=30, output_chunk_length=1, objective="mape")
lgbm_model_m4.fit(m4_train)

tic = time.time()
preds = lgbm_model_m4.predict(n=HORIZON, series=air_train)
lgbm_time_transfer = time.time() - tic

lgbm_smapes_transfer = eval_forecasts(preds, air_test)

Finally, let’s plot these new results as well:

 

线性回归也提供了相当不错的性能。它的速度稍慢一些，可能只是因为 N-BEATS 的推理是跨时间序列批次高效批处理的，并且在 GPU 上执行。

回顾：在 M3 数据集上使用相同的模型

好了，现在，我们用航空乘客数据集测试一下结果怎么样？让我们在新的数据集上重复整个过程看看效果 :) 你会发现，实际上只需要几行代码。我们将使用 M3 预测竞赛中的 1,400 个月序列作为新的“测试”数据集。以下是运行和测试所有模型所需的全部代码：

 

# load M3 dataset
m3_train, m3_test = load_m3()

# naive last
naive1_smapes_m3, naive1_time_m3 = eval_local_model(
    m3_train, m3_test, NaiveSeasonal, K=1
)

# naive seasonal
naive12_smapes_m3, naive12_time_m3 = eval_local_model(
    m3_train, m3_test, NaiveSeasonal, K=12
)

# Exponential smoothing
ets_smapes_m3, ets_time_m3 = eval_local_model(m3_train, m3_test, ExponentialSmoothing)

# Theta
theta_smapes_m3, theta_time_m3 = eval_local_model(m3_train, m3_test, Theta)

# ARIMA
arima_smapes_m3, arima_time_m3 = eval_local_model(
    m3_train, m3_test, ARIMA, p=12, d=1, q=0
)

# Kalman filter
kf_smapes_m3, kf_time_m3 = eval_local_model(
    m3_train, m3_test, KalmanForecaster, dim_x=12
)

# Linear regression
lr_smapes_m3, lr_time_m3 = eval_global_model(
    m3_train, m3_test, LinearRegressionModel, lags=30, output_chunk_length=1
)

# LGBM
lgbm_smapes_m3, lgbm_time_m3 = eval_global_model(
    m3_train, m3_test, LightGBMModel, lags=35, output_chunk_length=1, objective="mape"
)

# Get forecasts with our pre-trained N-BEATS
start_time = time.time()
preds = nbeats_model_m4.predict(series=m3_train, n=HORIZON)
nbeats_m4_elapsed_time_m3 = time.time() - start_time
nbeats_m4_smapes_m3 = eval_forecasts(preds, m3_test)

# Get forecasts with our pre-trained linear regression model
start_time = time.time()
preds = lr_model_m4.predict(series=m3_train, n=HORIZON)
lr_m4_elapsed_time_m3 = time.time() - start_time
lr_m4_smapes_m3 = eval_forecasts(preds, m3_test)

# Get forecasts with our pre-trained LightGBM model
start_time = time.time()
preds = lgbm_model_m4.predict(series=m3_train, n=HORIZON)
lgbm_m4_elapsed_time_m3 = time.time() - start_time
lgbm_m4_smapes_m3 = eval_forecasts(preds, m3_test)

 现在，对它们进行比较：

 

预训练的 N-BEATS 模型也获得了合理的准确率，尽管不如最准确的模型。需要注意的是，在 3 个最准确的模型中，有两个模型（指数平滑法和卡尔曼滤波器）在用于航空旅客序列时表现不佳。ARIMA 表现最佳，但速度比 N-BEATS 慢约 170 倍，后者无需任何训练，每个时间序列大约需要 15 毫秒即可生成预测结果。需要注意的是，这个 N-BEATS 模型从未在我们要求它预测的任何序列上进行过训练。

结论

迁移学习和元学习在时间序列预测领域无疑是一条充满趣味却尚未被充分探索的路径。它们何时能够大显身手？何时可能遭遇滑铁卢？微调操作是否真的能雪中送炭？究竟该在怎样的场景下启用它们？这些问题仍有许多等待破解，但我希望通过实际验证表明，借助 Darts 模型能够轻松开启相关领域的探索之旅。

那么，究竟哪种方法最契合你的应用场景呢？和往常一样，答案取决于具体情况。如果你主要面对的是拥有充足历史记录的孤立序列，那么像 ARIMA 这样的经典方法将大有用武之地。即便处理更大规模的数据集，倘若计算能力并非瓶颈，这类方法也能为单变量序列提供实用且易于上手的解决方案。另一方面，若你需要处理海量序列或多变量序列，机器学习方法与全局模型往往是更优选择 —— 它们能够精准捕捉不同时间序列中的模式规律，并且通常具备更高的运行效率。千万不要小觑基于线性回归的模型！倘若你有理由相信需要捕捉更为复杂的模式，或者推理速度对你而言至关重要，那么不妨大胆尝试深度学习方法。N - BEATS 已在元学习场景中展现出独特价值，但这种创新思路同样可能适用于其他模型。