目前最详细的模型校准讲解：面向初学者（带代码示例的可视化指南）

最新推荐文章于 2025-05-23 10:18:27 发布

我不是小upper

最新推荐文章于 2025-05-23 10:18:27 发布

阅读量814

点赞数 12

分类专栏：数据科学机器学习文章标签：人工智能机器学习

本文链接：https://blog.csdn.net/qq_70350287/article/details/148125341

版权

数据科学同时被 2 个专栏收录

56 篇文章

订阅专栏

机器学习

39 篇文章

订阅专栏

如果你已经训练了多个分类模型，它们似乎都表现良好，准确率也很高。那么恭喜你！

但是等等，一个模型真的比其他模型更好吗？单凭准确率并不能说明全部问题。如果一个模型持续高估其置信度，而另一个模型却低估了它，该怎么办？这时就需要模型校准了。

在这里，我们将了解什么是模型校准，并探索如何评估模型预测的可靠性——我们将使用视觉效果和实际代码示例来展示如何识别校准问题。准备好超越准确性，激发机器学习模型的真正潜力！

了解校准

模型校准衡量的是模型预测概率与实际性能的匹配程度。一个概率得分为 70% 的模型，对于类似的预测，应该有 70% 的正确率。这意味着它的概率得分应该反映其预测正确的真实可能性。

校准为何重要

准确度告诉我们一个模型总体上正确的频率，而校准度则告诉我们是否可以信任它的概率得分。两个模型可能都具有 90% 的准确度，但其中一个模型可能给出切合实际的概率得分，而另一个模型则给出过于自信的预测。在许多实际应用中，拥有可靠的概率得分与拥有正确的预测同样重要。

两个准确率相同（70% 正确）的模型，其预测结果的置信度却有所不同。模型 A 使用平衡概率得分（0.3 和 0.7），而模型 B 仅使用极端概率（0.0 和 1.0），表明它对每个预测要么完全确定，要么完全不确定。

完美校准与现实

一个完美校准的模型，其预测概率和实际成功率应该直接匹配：当它以 90% 的概率进行预测时，它应该在 90% 的时间内是正确的。这同样适用于所有概率水平。

然而，大多数模型并非完美校准。它们可能是：

过度自信：给出的概率分数相对于实际表现来说过高
缺乏自信：给出的概率分数相对于他们的实际表现来说太低
两者皆有：在某些方面过于自信，而在其他方面则缺乏自信

四个准确率相同（70%）的模型显示出不同的校准模式。过度自信的模型会做出极端预测（0.0 或 1.0），而缺乏信心的模型则保持在 0.5 左右。过度自信和缺乏信心的模型会在极端值和中间值之间切换。校准良好的模型会使用与其实际性能相匹配的合理概率（“否”为 0.3，“是”为 0.7）。

预测概率与实际正确性之间的不匹配，可能导致在实际应用中使用这些模型时做出错误的决策。因此，理解和改进模型校准对于构建可靠的机器学习系统至关重要。

📊 使用的数据集

为了探索模型校准，我们将继续使用我在之前关于分类算法的文章中使用的相同数据集：根据天气状况预测某人是否会打高尔夫球。

列：“阴天（独热编码为 3 列）”、“温度”（华氏度）、“湿度”（百分比）、“有风”（是/否）和“播放”（是/否，目标特征）

import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split

# Create and prepare dataset
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast', 
                'sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy',
                'sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast',
                'rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
                   72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
                   88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
                 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
                 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True,
             True, False, True, True, False, False, True, False, True, True, False,
             True, False, False, True, False, False],
    'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes',
             'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes',
             'Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}
# Prepare data
df = pd.DataFrame(dataset_dict)

在训练模型之前，我们通过对分类特征进行了转换。这些预处理步骤确保所有模型都能有效地利用数据，同时保持数据之间的公平比较。

from sklearn.preprocessing import StandardScaler
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)

# Rearrange columns
column_order = ['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind', 'Play']
df = df[column_order]

# Prepare features and target
X,y = df.drop('Play', axis=1), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

# Scale numerical features
scaler = StandardScaler()
X_train[['Temperature', 'Humidity']] = scaler.fit_transform(X_train[['Temperature', 'Humidity']])
X_test[['Temperature', 'Humidity']] = scaler.transform(X_test[['Temperature', 'Humidity']])

模型与训练

为了进行此次探索，我们训练了四种分类模型，以获得相似的准确度分数：

K最近邻（kNN）
伯努利朴素贝叶斯
逻辑回归
多层感知器（MLP）

虽然这些模型在这个简单的问题上实现了相同的准确度，但它们计算预测概率的方式不同。

尽管这四个模型的正确率为 85.7%，但它们的预测结果却呈现出不同的置信度。其中，MLP 模型倾向于对其答案非常确定（给出接近 1.0 的值），而 kNN 模型则更为谨慎，给出的置信度分数差异更大。

import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
from sklearn.naive_bayes import BernoulliNB

# Initialize the models with the found parameters
knn = KNeighborsClassifier(n_neighbors=4, weights='distance')
bnb = BernoulliNB()
lr = LogisticRegression(C=1, random_state=42)
mlp = MLPClassifier(hidden_layer_sizes=(4, 2),random_state=42, max_iter=2000)

# Train all models
models = {
    'KNN': knn,
    'BNB': bnb,
    'LR': lr,
    'MLP': mlp
}

for name, model in models.items():
    model.fit(X_train, y_train)

# Create predictions and probabilities for each model
results_dict = {
    'True Labels': y_test
}

for name, model in models.items():
#    results_dict[f'{name} Pred'] = model.predict(X_test)
    results_dict[f'{name} Prob'] = model.predict_proba(X_test)[:, 1]

# Create results dataframe
results_df = pd.DataFrame(results_dict)

# Print predictions and probabilities
print("\nPredictions and Probabilities:")
print(results_df)

# Print accuracies
print("\nAccuracies:")
for name, model in models.items():
    accuracy = accuracy_score(y_test, model.predict(X_test))
    print(f"{name}: {accuracy:.3f}")

通过这些差异，我们将探讨为什么我们需要超越准确性。

测量校准

为了评估模型预测概率与其实际性能的匹配程度，我们使用了多种方法和指标。这些测量有助于我们了解模型的置信度是否可靠。

布莱尔评分(Brier Score)

布莱尔评分衡量的是预测概率与实际结果之间的均方差。其范围从0到1，分数越低，校准效果越好。该评分尤其有用，因为它同时考虑了校准和准确性。

分数 (0.148) 表明模型的置信度与其实际表现的匹配程度。该分数是通过比较模型预测的概率与实际发生的情况得出的（0 表示“否”，1 表示“是”），差异越小，预测效果越好。

对数损失

对数损失计算正确预测的负对数概率。该指标对自信但错误的预测尤其敏感——当一个模型声称它有 90% 的把握但预测错误时，它受到的惩罚比 60% 的把握但预测错误时要大得多。值越低，校准效果越好。

对于每个预测，它会考察模型对正确答案的信心程度。当模型非常自信但错误时（例如索引 26），它会受到更大的惩罚。最终得分 0.455 是所有这些惩罚的平均值，数字越低，预测越好。

预期校准误差 (ECE)

ECE测量预测概率与实际概率（取标签平均值）之间的平均差异，并根据每个概率组中有多少预测进行加权。该指标有助于我们了解模型在概率估计中是否存在系统性偏差。

根据模型的置信度，预测结果被分为 5 个区间。对于每一组，我们会将模型的平均置信度与其实际正确的概率进行比较。最终得分 (0.1502) 告诉我们这些匹配程度如何，数值越低越好。

可靠性图

与 ECE 类似，可靠性图（或校准曲线）通过将预测结果分箱并与实际结果进行比较，从而直观地展现模型校准。ECE 给出一个衡量校准误差的数值，而可靠性图则以图形方式向我们展示相同的信息。我们使用相同的分箱方法，并计算每个箱体中正结果的实际频率。绘制这些点后，它们会准确地显示出模型预测结果与完美校准结果的偏差，最终呈现为一条对角线。

与 ECE 类似，预测结果根据置信度分为 5 个区间。每个点表示模型实际正确率（上/下）与其置信度（左/右）的比较情况。虚线表示完全匹配——模型曲线表明它有时会认为自己比实际情况更好或更差。

比较校准指标

每个指标都显示了校准问题的不同方面：

较高的 Brier 分数表明总体概率估计较差。
高对数损失表明过度自信的错误预测。
较高的 ECE 表明概率估计存在系统性偏差。

综合起来，这些指标为我们提供了完整的图景，让我们了解模型的概率分数如何反映其真实性能。

构建我们的模型

对于我们的模型，让我们计算校准指标并绘制它们的校准曲线：

from sklearn.metrics import brier_score_loss, log_loss
from sklearn.calibration import calibration_curve
import matplotlib.pyplot as plt

# Initialize models
models = {
    'k-Nearest Neighbors': KNeighborsClassifier(n_neighbors=4, weights='distance'),
    'Bernoulli Naive Bayes': BernoulliNB(),
    'Logistic Regression': LogisticRegression(C=1.5, random_state=42),
    'Multilayer Perceptron': MLPClassifier(hidden_layer_sizes=(4, 2), random_state=42, max_iter=2000)
}

# Get predictions and calculate metrics
metrics_dict = {}
for name, model in models.items():
    model.fit(X_train, y_train)
    y_prob = model.predict_proba(X_test)[:, 1]
    metrics_dict[name] = {
        'Brier Score': brier_score_loss(y_test, y_prob),
        'Log Loss': log_loss(y_test, y_prob),
        'ECE': calculate_ece(y_test, y_prob),
        'Probabilities': y_prob
    }

# Plot calibration curves
fig, axes = plt.subplots(2, 2, figsize=(8, 8), dpi=300)
colors = ['orangered', 'slategrey', 'gold', 'mediumorchid']

for idx, (name, metrics) in enumerate(metrics_dict.items()):
    ax = axes.ravel()[idx]
    prob_true, prob_pred = calibration_curve(y_test, metrics['Probabilities'], 
                                           n_bins=5, strategy='uniform')
    
    ax.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
    ax.plot(prob_pred, prob_true, color=colors[idx], marker='o', 
            label='Calibration curve', linewidth=2, markersize=8)
    
    title = f'{name}\nBrier: {metrics["Brier Score"]:.3f} | Log Loss: {metrics["Log Loss"]:.3f} | ECE: {metrics["ECE"]:.3f}'
    ax.set_title(title, fontsize=11, pad=10)
    ax.grid(True, alpha=0.7)
    ax.set_xlim([-0.05, 1.05])
    ax.set_ylim([-0.05, 1.05])
    ax.spines[['top', 'right', 'left', 'bottom']].set_visible(False)
    ax.legend(fontsize=10, loc='upper left')

plt.tight_layout()
plt.show()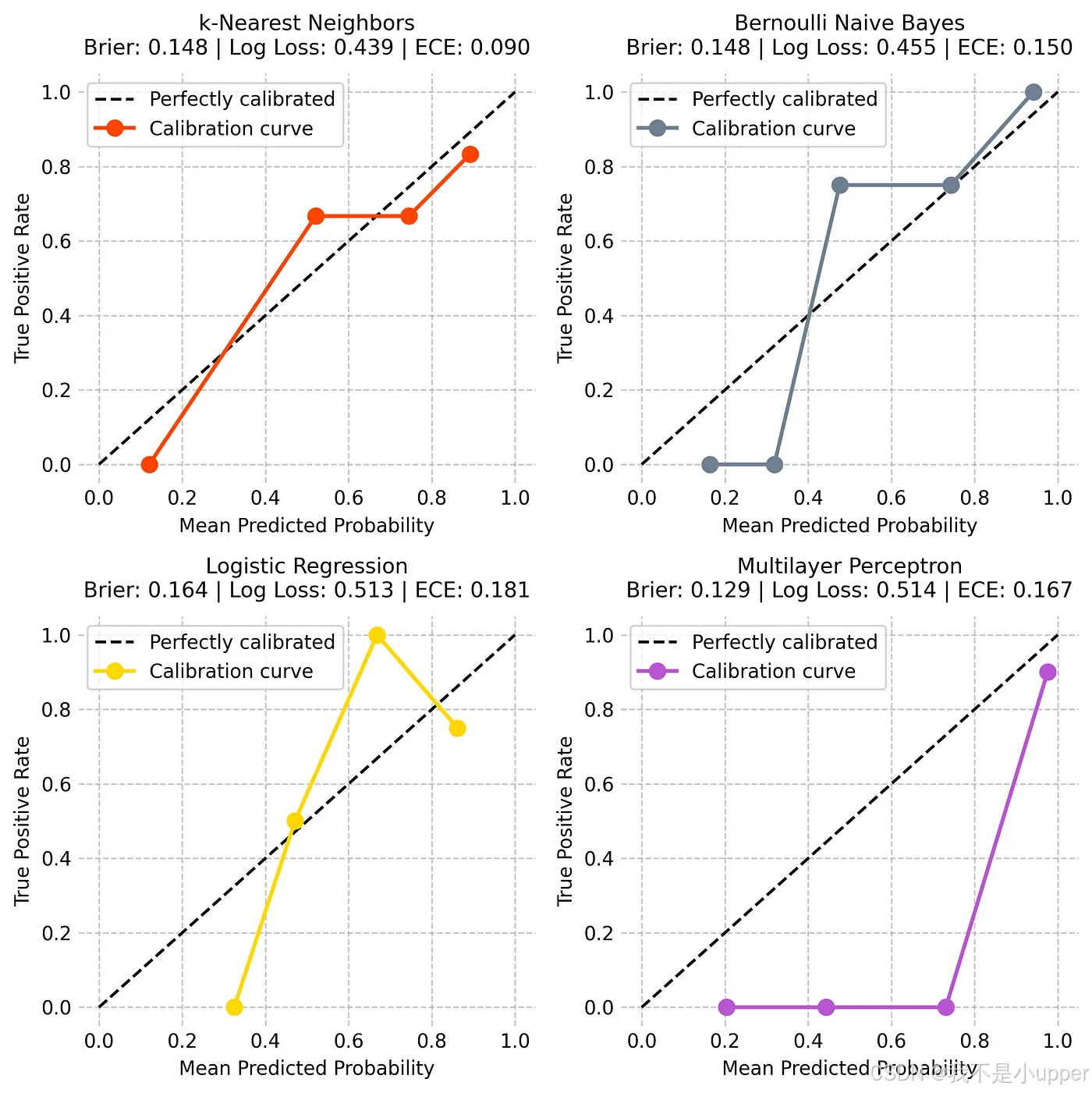

现在，让我们根据这些指标分析每个模型的校准性能：

k-最近邻 (KNN) 模型在估计其预测结果的确定性方面表现良好。其曲线与虚线保持接近，表明其性能良好。该模型得分较高——Brier 得分为 0.148，ECE 得分最高为 0.090。虽然有时它在中间范围内表现出过高的置信度，但通常情况下，它能够对其确定性做出可靠的估计。

伯努利朴素贝叶斯模型的曲线呈现出一种不寻常的阶梯状模式。这意味着它在不同的确定性水平之间跳跃，而不是平滑地变化。虽然它的布里尔得分与 KNN 相同（0.148），但其更高的 ECE（0.150）表明其在估计确定性方面的准确性较低。该模型在过于自信和不够自信之间切换。

逻辑回归模型的预测结果存在明显问题。它的直线偏离虚线较远，这意味着它经常误判其确定性。它的 ECE 得分最差（0.181），Brier 得分也很差（0.164）。该模型始终对其预测结果过于自信，因此不可靠。

多层感知器表现出一个明显的问题。尽管拥有最高的 Brier 得分（0.129），但它的线显示，它大多做出极端的预测——要么非常确定，要么非常不确定，很少有介于两者之间的预测。它较高的 ECE（0.167）和中间范围内的平坦线表明，它难以做出平衡的确定性估计。

在检验了所有四个模型之后，k最近邻在预测确定性估计方面显然表现最佳。它在不同确定性水平上保持一致的性能，并在预测中展现出最可靠的模式。虽然其他模型在某些指标上可能得分较高（例如多层感知器的Brier得分），但它们的图表表明，当我们需要信任它们的确定性估计时，它们的可靠性并不高。

结语

在选择不同的模型时，我们需要同时考虑它们的准确性和校准质量。准确率略低但校准效果较好的模型可能比准确率高但概率估计较差的模型更有价值。

通过了解校准及其重要性，我们可以构建更可靠的机器学习系统，用户不仅可以信任他们的预测，还可以信任他们对这些预测的信心。

🌟 模型校准代码总结（1 个模型）

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import BernoulliNB
from sklearn.metrics import brier_score_loss, log_loss
from sklearn.calibration import calibration_curve
import matplotlib.pyplot as plt

# Define ECE
def calculate_ece(y_true, y_prob, n_bins=5):
    bins = np.linspace(0, 1, n_bins + 1)
    ece = 0
    for bin_lower, bin_upper in zip(bins[:-1], bins[1:]):
        mask = (y_prob >= bin_lower) & (y_prob < bin_upper)
        if np.sum(mask) > 0:
            bin_conf = np.mean(y_prob[mask])
            bin_acc = np.mean(y_true[mask])
            ece += np.abs(bin_conf - bin_acc) * np.sum(mask)
    return ece / len(y_true)

# Create dataset and prepare data
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast','sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy','sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast','rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True,True, False, True, True, False, False, True, False, True, True, False,True, False, False, True, False, False],
    'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes','Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes','Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}

# Prepare and encode data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
df = df[['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind', 'Play']]

# Split and scale data
X, y = df.drop('Play', axis=1), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
scaler = StandardScaler()
X_train[['Temperature', 'Humidity']] = scaler.fit_transform(X_train[['Temperature', 'Humidity']])
X_test[['Temperature', 'Humidity']] = scaler.transform(X_test[['Temperature', 'Humidity']])

# Train model and get predictions
model = BernoulliNB()
model.fit(X_train, y_train)
y_prob = model.predict_proba(X_test)[:, 1]

# Calculate metrics
metrics = {
    'Brier Score': brier_score_loss(y_test, y_prob),
    'Log Loss': log_loss(y_test, y_prob),
    'ECE': calculate_ece(y_test, y_prob)
}

# Plot calibration curve
plt.figure(figsize=(6, 6), dpi=300)
prob_true, prob_pred = calibration_curve(y_test, y_prob, n_bins=5, strategy='uniform')

plt.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
plt.plot(prob_pred, prob_true, color='slategrey', marker='o', 
        label='Calibration curve', linewidth=2, markersize=8)

title = f'Bernoulli Naive Bayes\nBrier: {metrics["Brier Score"]:.3f} | Log Loss: {metrics["Log Loss"]:.3f} | ECE: {metrics["ECE"]:.3f}'
plt.title(title, fontsize=11, pad=10)
plt.grid(True, alpha=0.7)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.gca().spines[['top', 'right', 'left', 'bottom']].set_visible(False)
plt.legend(fontsize=10, loc='lower right')

plt.tight_layout()
plt.show()

🌟 模型校准代码总结（4 个模型）

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import BernoulliNB
from sklearn.linear_model import LogisticRegression
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import brier_score_loss, log_loss
from sklearn.calibration import calibration_curve
import matplotlib.pyplot as plt

# Define ECE
def calculate_ece(y_true, y_prob, n_bins=5):
    bins = np.linspace(0, 1, n_bins + 1)
    ece = 0
    for bin_lower, bin_upper in zip(bins[:-1], bins[1:]):
        mask = (y_prob >= bin_lower) & (y_prob < bin_upper)
        if np.sum(mask) > 0:
            bin_conf = np.mean(y_prob[mask])
            bin_acc = np.mean(y_true[mask])
            ece += np.abs(bin_conf - bin_acc) * np.sum(mask)
    return ece / len(y_true)

# Create dataset and prepare data
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast','sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy','sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast','rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True,True, False, True, True, False, False, True, False, True, True, False,True, False, False, True, False, False],
    'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes','Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes','Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}

# Prepare and encode data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
df = df[['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind', 'Play']]

# Split and scale data
X, y = df.drop('Play', axis=1), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
scaler = StandardScaler()
X_train[['Temperature', 'Humidity']] = scaler.fit_transform(X_train[['Temperature', 'Humidity']])
X_test[['Temperature', 'Humidity']] = scaler.transform(X_test[['Temperature', 'Humidity']])

# Initialize models
models = {
    'k-Nearest Neighbors': KNeighborsClassifier(n_neighbors=4, weights='distance'),
    'Bernoulli Naive Bayes': BernoulliNB(),
    'Logistic Regression': LogisticRegression(C=1.5, random_state=42),
    'Multilayer Perceptron': MLPClassifier(hidden_layer_sizes=(4, 2), random_state=42, max_iter=2000)
}

# Get predictions and calculate metrics
metrics_dict = {}
for name, model in models.items():
    model.fit(X_train, y_train)
    y_prob = model.predict_proba(X_test)[:, 1]
    metrics_dict[name] = {
        'Brier Score': brier_score_loss(y_test, y_prob),
        'Log Loss': log_loss(y_test, y_prob),
        'ECE': calculate_ece(y_test, y_prob),
        'Probabilities': y_prob
    }

# Plot calibration curves
fig, axes = plt.subplots(2, 2, figsize=(8, 8), dpi=300)
colors = ['orangered', 'slategrey', 'gold', 'mediumorchid']

for idx, (name, metrics) in enumerate(metrics_dict.items()):
    ax = axes.ravel()[idx]
    prob_true, prob_pred = calibration_curve(y_test, metrics['Probabilities'], 
                                           n_bins=5, strategy='uniform')
    
    ax.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
    ax.plot(prob_pred, prob_true, color=colors[idx], marker='o', 
            label='Calibration curve', linewidth=2, markersize=8)
    
    title = f'{name}\nBrier: {metrics["Brier Score"]:.3f} | Log Loss: {metrics["Log Loss"]:.3f} | ECE: {metrics["ECE"]:.3f}'
    ax.set_title(title, fontsize=11, pad=10)
    ax.grid(True, alpha=0.7)
    ax.set_xlim([-0.05, 1.05])
    ax.set_ylim([-0.05, 1.05])
    ax.spines[['top', 'right', 'left', 'bottom']].set_visible(False)
    ax.legend(fontsize=10, loc='upper left')

plt.tight_layout()
plt.show()