写在前面
本文主要是学习sutton的书--强化学习绪论部分的整理,这里为了更好地理解,扩展了一些书上的内容。例子来源于网上,后续介绍的时候我会加上来源;还有部分PPT内容参考台大李宏毅老师的PPT以及Google DeepMind的David Silver的PPT,后续会注明!~~一、强化学习概念
1、基本概念
在进入强化学习之前,这里先讲一个例子:
小时候刚上学的时候,第一天老师布置了作业,我很认真地完成了它,然后得到了一朵小红花;第二天老师布置了作业,我没有完成作业,然后老师批评了我。那么,第三天,老师仍旧布置了作业,我们肯定是倾向于认真完成作业,因为这样可以得到一朵小红花。
强化学习的思想和小孩子不断学习的过程是类似的,强化学习就是希望智能体可以像人一样,在不断地试错过程中,从经验中学习。
下面来看一下强化学习的概念:
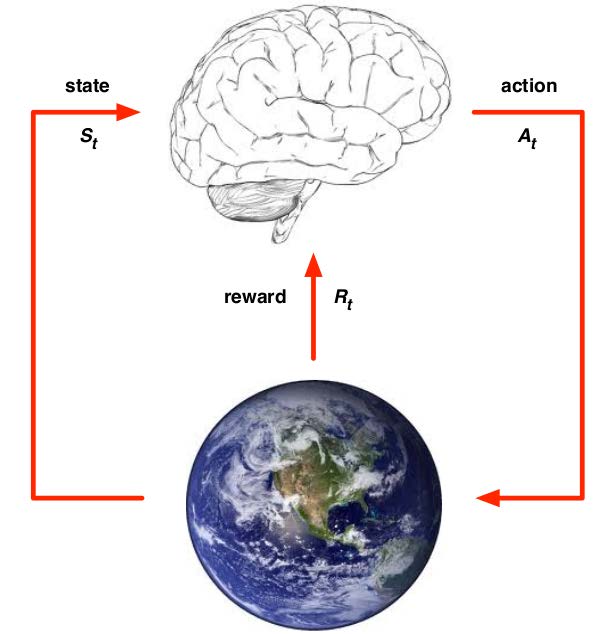
我们先来看下强化学习过程中涉及到的几个概念,如上图强化学习过程所示(图片来源于网上,不记得具体地址了):
- state:状态,也称为observation
- action:行动
- reward:奖励
- agent:智能体,主要作用为:(1)执行action A t A_t At;(2)接收state S t S_t St;(3)接收来自环境的reward R t R_t Rt
- environment:环境,主要作用为:(1)接收action A t A_t At;(2)给出state S t + 1 S_{t+1} St+1;(3)给出reward R t + 1 R_{t+1} Rt+1
为了更清晰地表达上述过程,下面来看一个例子(图片来自李宏毅老师):
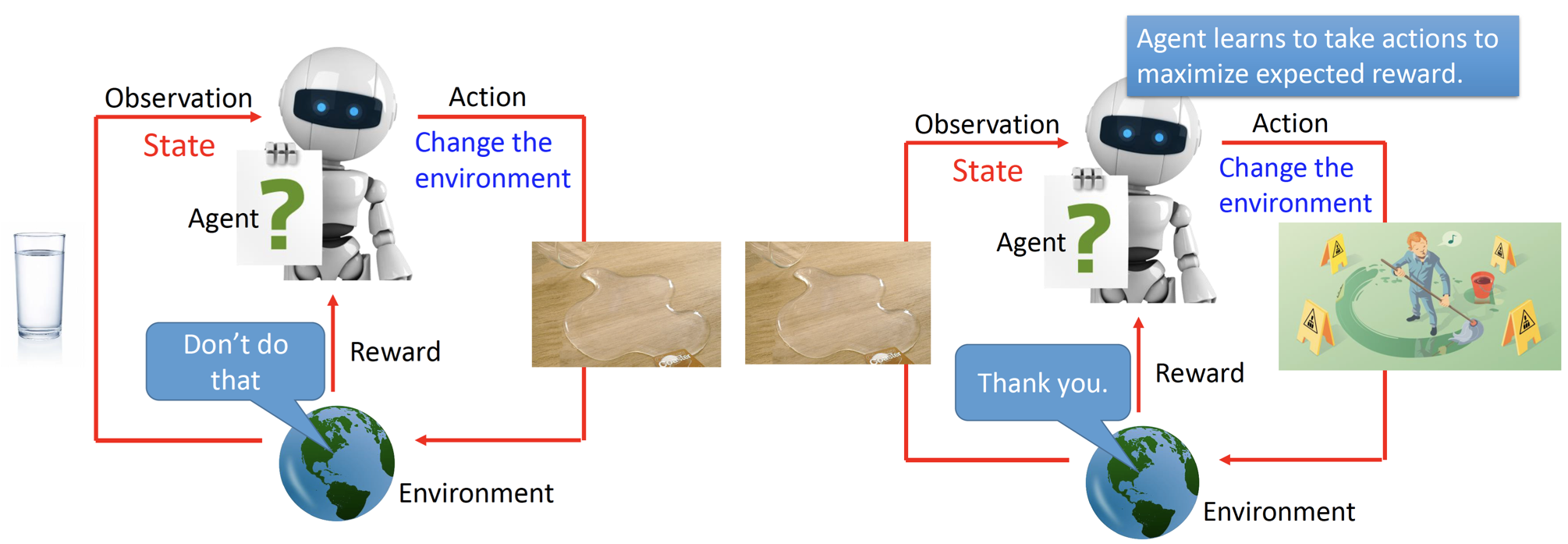
1)在左图中,Agent观察到当前的state是桌子上有一个水杯,然后采取了action:将水杯碰倒,于是environment观察到了最新的情况,给了agent一个负的reward。
2)在右图中,因为水杯已经碰倒了,所以Agent看到的的state是水洒掉了,基于当前的state,Agent做出决策:用拖把把水清理掉,然后environment观察到了最新的情况,给了agent一个正向的reward。
3)上述过程不断反复,在不断的试错过程中,Agent知道下次如果地上有脏东西,我就需要把他清理掉,即Agent在不断地试错过程中,从经验中学习。
2、核心思想
- 与环境交互
- 从经验中学习
- RL的目标是最大化累积奖励的期望
上面RL的目标为什么是累积奖励期望最大化呢,这是因为RL基于奖励假说,具体如下:
在时间t,state为S的情况下,累积奖励的期望如下:
V
(
S
)
=
E
π
[
G
t
∣
S
]
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
.
.
.
.
(
γ
∈
[
0
,
1
)
)
\begin{aligned} & V(S) = E_\pi[G_t | S] \\ & G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + .... (\gamma \in [0, 1)) \end{aligned}
V(S)=Eπ[Gt∣S]Gt=Rt+1+γRt+2+γ2Rt+3+....(γ∈[0,1))
γ \gamma γ又叫做折扣因子,它可以用来控制长期收益和短期收益的重要性,若 γ \gamma γ比较大,则说明我们更重视长期收益。在RL中,我们借助蒙特卡洛的思想:使用经验平均来代替随机变量的期望,即我们基于采样的思想来不断求解价值的值,当然后续为了改进,有基于时序差分的方法(这点看强化学习举例可以更清楚的理解)。
3、强化学习要素
强化学习主要有四个要素:policy(策略)、reward signal(奖励信息)、value function(价值函数)、model(模型,optional)
- policy
π
θ
(
A
∣
S
)
\pi_\theta(A|S)
πθ(A∣S)
- policy就是agent的一个行为信息,即agent决定在当前state下应该采取什么样的action
- 它是一个从state到action的映射,可以是一个函数或者是以查表的方式。
- reward signal
R
(
S
,
A
)
R(S, A)
R(S,A)
- 奖励机制只采取某个action之后环境给出的奖励,是短期的一个概念
- 奖励是改变policy的主要因素,如果采取某个action之后得到了负向的reward,则在之后agent采取action的时候应该避免这个action。
- value function
V
(
S
)
V(S)
V(S)
- 价值是对从当前到未来奖励的预测,是一个长期的概念。
- 价值用来衡量状态的好坏,我们在采取行动时应该选择价值最大的action。
- model(optional)
- 模型是可选的,在model-free的RL算法中,是没有model这个要素的
- 模型是对环境的建模,也就是说,如果模型建模完成之后,我们可以得到以下概率:
- P s s ′ a = P [ S ′ ∣ S , A ] \mathcal{P}_{ss'}^a=P[S'|S,A] Pss′a=P[S′∣S,A],即在当前S和A的情况下,下一个state S’的概率。
- R s a = P [ R ′ ∣ S , A ] \mathcal{R}_{s}^a=P[R'|S,A] Rsa=P[R′∣S,A],即在当前S和A的情况下,下一个reward R’的概率。
二、强化学习举例
例子详见:path-finding-q-learning-tutorial
中文翻译见:A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)
说明:这个例子在讲解的时候都是以Q-learning为例的,但是我个人觉得 Q ( S , A ) Q(S,A) Q(S,A)的更新公式不是Q-learning的更新公式,所以我个人觉得把它当做一个了解强化学习的例子来看比较好理解。
三、RL限制
强化学习有两个限制:
- Reward delay 奖励延迟的问题,即对于有些任务来说,获取的奖励是具有延迟的,不能很好地反应action的效果,下面看下面的例子,会更清晰。
- 打游戏:在玩游戏的时候,只有“Fire”才会得到奖励,但是其实“Fire”之前的左右移动对“Fire”的动作是很重要的。
- 玩围棋:玩围棋的时候,只有下到最后的时候才知道是输是赢,但是其实下棋的每一步都对最后的结果有很大影响的。
- Exploration & Exploitation 探索与利用的问题。探索是指我们想要挖掘环境中更多的信息;利用是指想要使用当前环境中已有的最大的价值的行动。看下面的两个例子更好的理解这个问题。
- 餐馆选择:在选择餐馆的时候,利用是指选择我们去过的最喜欢的餐馆;探索是指选择一个新的餐馆,可以去过这个新的餐馆之后可能会发现这个新餐馆也是蛮不错的。
- 在线广告:在设置广告的时候,利用是指展示最成功的广告,即利用广告与用户的相关性推荐;探索指推荐不同的或者随机推荐广告,这可以挖掘用户的潜在兴趣。
四、RL分类
本部分将讲解强化学习从三个角度的分类情况。
1、Model-free vs. Model-based
Model-free和Model-based的最大区别是是否对周围环境建模。
- Model-free:学习最优的策略,如Q-learning、Sarsa、Policy-gradient、DQN和A3C
- Model-based:对环境建模,基于此模型,选择一个最优的策略。
如下图所示,model-free是Agent在真实环境中不断学习,而对于model-based,其先对环境建模,而后基于建模后的模拟环境进行学习:
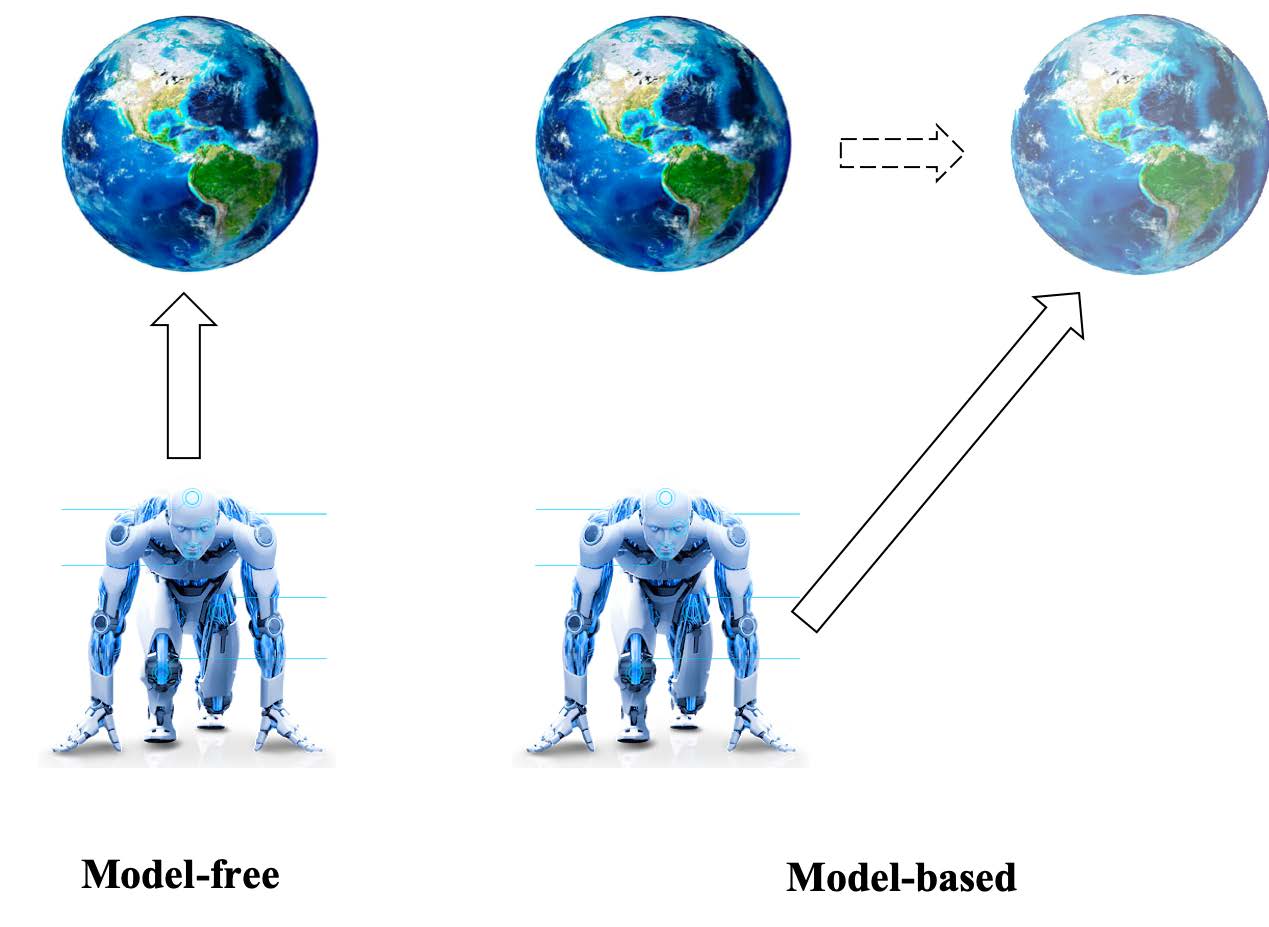
注意:
model-free的方法是通过不断试错、不断学习,通过不断与环境交互得到下一个应该执行的action。
model-based的方法因为已对模型建模过,所以是可以直接获得在当前的state和action情况下,一个state S’和下一个reward R’的概率的,所以直接决策就可以(这两个概率在model要素的定义中有)。
举例来说,在玩游戏的时候,对于新手来说,不知道该往哪个地方走,我不知道前面的障碍物需要清理掉还是绕过去,需要通过不断试错来寻求经验,这便是model-free算法的学习方式。而对于有经验的游戏玩家来说,他已经清楚的知道了地图,知道这个地方需要绕过还是清理,直接选取对应的行动就可以,而不用通过与环境的不断交互来学习经验,这便是model-based算法的学习方式。
2、Value-based vs. Policy-based
- Value-based:
Value-based的算法步骤为:(1)在策略评估阶段,不断学习action的价值(2)在策略优化阶段,基于价值选择最合适的action。Value-based的方法有Q-learning、Sarsa、DQN等。 - Policy-based:
Policy-based的算法步骤为:学习一个策略函数,这样在选择action的时候不需要基于价值函数,而是直接基于策略函数。Policy-based的方法有Policy-gradient、A3C、DDPG等。
注意:在学习策略参数的时候可能会用到价值函数,但是基于Policy的算法在选择action的时候不会使用价值函数。
进一步地来分析,Vaue-based的算法首先得到
Q
π
(
S
,
A
)
Q_{\pi}(S, A)
Qπ(S,A),而后得到策略:
π
∗
=
arg max
π
Q
π
(
S
,
A
)
\pi_{*} = \argmax_{\pi} Q_{\pi}(S, A)
π∗=πargmaxQπ(S,A)
而对于Policy-based的算法,通过优化长期收益得到policy函数,如下所示:
J
(
θ
)
=
∑
S
∈
S
d
π
(
θ
)
(
S
)
V
π
(
θ
)
(
S
)
=
∑
S
∈
S
(
d
π
(
θ
)
∑
A
∈
A
π
(
A
∣
S
,
θ
)
Q
π
(
S
,
A
)
)
\begin{aligned} J(\theta) &= \sum_{S \in \mathcal{S}} d_{\pi(\theta)}(S)V_{\pi(\theta)}(S) \\ &= \sum_{S \in \mathcal{S}} (d_{\pi(\theta)} \sum_{A \in \mathcal{A}} \pi(A|S,\theta)Q_{\pi}(S,A)) \end{aligned}
J(θ)=S∈S∑dπ(θ)(S)Vπ(θ)(S)=S∈S∑(dπ(θ)A∈A∑π(A∣S,θ)Qπ(S,A))
J ( θ ) J(\theta) J(θ)是目标函数,其含义是长期收益, d π ( θ ) ( S ) d_{\pi(\theta)}(S) dπ(θ)(S)是 V π ( θ ) ( S ) V_{\pi(\theta)}(S) Vπ(θ)(S)的稳态分布。这里说明 V ( S ) V(S) V(S)指状态 S S S的价值,而 Q ( S , A ) Q(S,A) Q(S,A)表示在状态为 S S S,行动为 A A A的情况下对应的价值。上式中policy π ( A ∣ S , θ ) \pi(A|S,\theta) π(A∣S,θ)是关于 θ \theta θ的分布,于是,现在目标函数 J ( θ ) J(\theta) J(θ)有了,我们需要求得 θ \theta θ的值,可以使用随机梯度下降等更新参数,当 θ \theta θ求解之后,policy的公式便得到了,于是我们可以基于此policy选取action。
因此从上面我们就可以看出,Value-based的的方法更适合于离散action space的情况;而Policy-based的方法更适合于连续action space的情况,当然Policy-based的算法也适合于离散action space的情况,但是Value-based的方法无法适用于连续action space的情况。
3、Off-policy vs. On-policy
在说明Off-policy和On-policy的区别之前,先看行为策略和目标策略的含义:
行为策略:指导用户产生与环境交互的行为
目标策略:评估状态和行动的价值
- Off-policy: 行为策略和目标策略不同。Off-policy的典型方法为Q-learning、DQN。
- On-policy: 行为策略和目标策略相同。On-policy的典型方法为:Sarsa。
下面以Q-learning和Sarsa为例具体说明行为策略和目标策略不同(Q-learning是Off-policy的代表,Sarsa是On-policy的代表):
Q-learning:
Q
(
S
,
A
)
←
Q
(
S
,
A
)
+
α
[
R
(
S
,
A
)
+
γ
max
a
Q
(
S
′
,
a
)
−
Q
(
S
,
A
)
]
=
(
1
−
α
)
Q
(
S
,
A
)
+
α
[
R
(
S
,
A
)
+
γ
max
a
Q
(
S
′
,
a
)
]
\begin{aligned} Q(S,A) &\leftarrow Q(S,A) + \alpha[R(S,A) + \gamma \max_aQ(S', a) - Q(S, A)] \\ &=(1-\alpha) Q(S, A) + \alpha [R(S,A) + \gamma \max_aQ(S', a)] \end{aligned}
Q(S,A)←Q(S,A)+α[R(S,A)+γamaxQ(S′,a)−Q(S,A)]=(1−α)Q(S,A)+α[R(S,A)+γamaxQ(S′,a)]
Sarsa:
Q
(
S
,
A
)
←
Q
(
S
,
A
)
+
α
[
R
(
S
,
A
)
+
γ
Q
(
S
′
,
A
′
)
−
Q
(
S
,
A
)
]
=
(
1
−
α
)
Q
(
S
,
A
)
+
α
[
R
(
S
,
A
)
+
γ
Q
(
S
′
,
A
′
)
]
\begin{aligned} Q(S,A) &\leftarrow Q(S,A) + \alpha[R(S,A) + \gamma Q(S', A') - Q(S, A)] \\ &=(1-\alpha) Q(S, A) + \alpha [R(S,A) + \gamma Q(S', A')] \end{aligned}
Q(S,A)←Q(S,A)+α[R(S,A)+γQ(S′,A′)−Q(S,A)]=(1−α)Q(S,A)+α[R(S,A)+γQ(S′,A′)]
上式是Q-learning和Sarsa的Q值更新公式,这里,S指state,A指action,S’指下一个state,A’是下一个action,我们可以看到的不同地方是 γ \gamma γ后面的表达式,注意:Q-learinng和Sarsa实际在选择行动的时候都是使用的 ϵ − \epsilon - ϵ−greedy算法,即以 ϵ \epsilon ϵ的概率选取价值最大的action,以 1 − ϵ 1 - \epsilon 1−ϵ的概率随机选取action。(这种策略为了保证探索与利用都同时考虑到)。
Q-learning更新 Q ( S , A ) Q(S, A) Q(S,A)的方法:使用是价值函数最大的action来更新;Sarsa更新 Q ( S , A ) Q(S, A) Q(S,A)使用的是实际选取的action。
整体上说,Q-learning的action选择策略是 ϵ − \epsilon - ϵ−greedy(行为策略),而 Q ( S , A ) Q(S, A) Q(S,A)的更新方法是使用最大价值对应的action(目标策略),因此行为策略和目标策略是不同的,所以是Q-learning是Off-policy的。Sarsa的action选择策略是 ϵ − \epsilon - ϵ−greedy(行为策略), Q ( S , A ) Q(S, A) Q(S,A)的更新使用的也是实际选择的action(目标策略),因此行为策略和目标策略是相同的,所以Sarsa是On-policy的。
(所以,在一定意义上来说,Q-learning是比较大胆的策略,始终使用最优值来更新 Q ( S , A ) Q(S, A) Q(S,A),而Sarsa是比较保守的策略。)
五、RL vs. Supervised vs. Unsupervised
- 无监督
无监督算法是挖掘数据中的隐含的数据结构等。 - 有监督学习
有监督学习类似于从老师这里学习,也就是找到映射问题。 - 强化学习
强化学习寻找反馈机制,即从经验中学习。
以围棋的例子来说,如果是监督学习,则若训练集中有3*3的方式,采取的行动是在(4,3)处下一个棋子,则在测试集中碰到这样的棋局,会采取在(4,3)处下一个棋子的行动,也就是跟着做;对于强化学习来说,先走第一步,接着第二步,一直到棋局结束,看结果是赢了还是输了,然后反过头来不断反思刚刚哪一步下的比较好,哪一步出现了问题,也就是从经验中不断学习(李宏毅老师的例子)。
六、工具包和实例
- RL使用的比较多的库是Gym和Universe
- 一个实例(来源于网上):flappybird
























 1775
1775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








