模拟上帝之手的对抗博弈——GAN背后的数学原理

作者：李乐 CSDN专栏作家

简介

深度学习的潜在优势就在于可以利用大规模具有层级结构的模型来表示相关数据所服从的概率密度。从深度学习的浪潮掀起至今，深度学习的最大成功在于判别式模型。判别式模型通常是将高维度的可感知的输入信号映射到类别标签。训练判别式模型得益于反向传播算法、dropout和具有良好梯度定义的分段线性单元。然而，深度产生式模型相比之下逊色很多。这是由于极大似然的联合概率密度通常是难解的，逼近这样的概率密度函数非常困难，而且很难将分段线性单元的优势应用到产生式模型的问题。

基于以上的观察，作者提出了产生对抗网络。顾名思义，产生对抗网络包含两个网络：产生器和判别器。产生器负责伪造一些数据，要求这些数据尽可能真实（尽可能服从只有上帝知道的概率分布），而判别器负责判别给定数据是伪造的（来自产生器生成的数据），还是来自由上帝创造的真实分布。至此，我们不得不佩服作者如此的问题形式化。整个过程中就是在博弈。产生器尽可能伪造出真实的数据，而判别器尽可能提高自身的判别性能。

这样一种问题形式化实际上是一种通用框架，因为判别器和生成器可以是任何一种深度模型。为了简单起见，该篇文章只利用多层感知机，而且生成器所生成的样本是由随机噪声得到的。利用这种方法，整个模型的训练融入了之前无法利用的反向传播算法和dropout. 这个过程中不需要近似推测和马尔科夫链。

产生对抗网络

这部分将具体介绍产生对抗网络模型，并详细推导出GAN的优化目标。

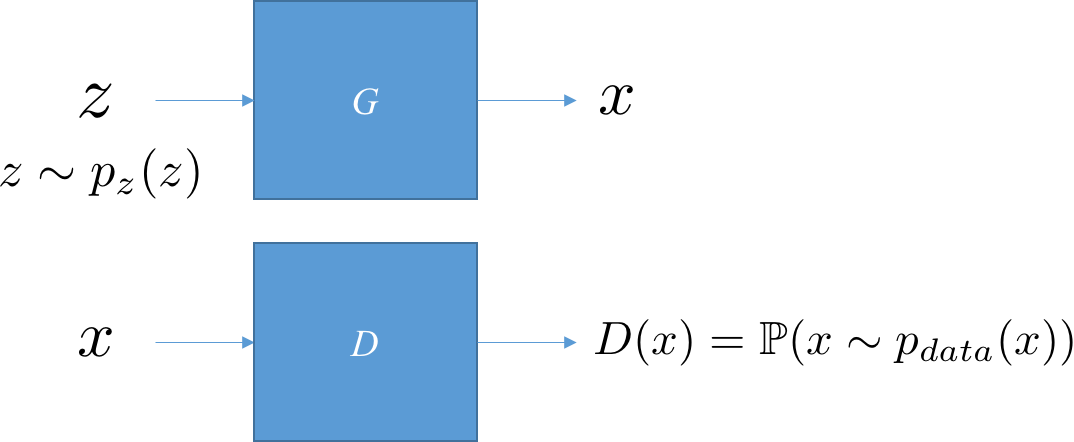
简单起见，生成器和判别器都基于多层感知神经元。对于生成器，我们希望它是一个由噪声到所希望生成数据的一个映射；对于判别器，它以被考查的数据作为输入，输出其服从上帝所定义的概率分布的概率值。下图清晰地展示了这个过程。

假设我们有包含m个样本的训练集S={ x(1),...,x(m)}. 此外，任给一种概率密度函数pz(z)（当然，在保证模型复杂度的前提下，相应的概率分布越简单越好），我们可以利用随机变量Z∼pz(z)采样得到m个噪声样本{ z(1),...,z(m)}. 由此，我们可以得到似然函数

L(x(1),...,x(m),z(1),...,z(m)|θg,θd)=∏i=1mD(x(i))I{ x(i)∈Data}(1−D(x(i)))I{ x(i)∉Data}∏j=1mD(G(x(j)))I{ G(x(j))∈Data}(1−D(G(x(j))))I{ G(x(j))∉Data}=∏i=1mD(x(i))∏j=1m(1−D(G(x(j))))

进一步，得到对数似然

logL=log⎛⎝∏i=1mD(x(i))∏j=1m(1−D(G(x(j))))⎞⎠=∑i=1mlogD(x(i))+∑j=1mlog(1−D(G(z(j))))

由大数定律，当m→∞时，我们用经验损失来近似期望损失，得

logL≈Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(x))]

回到我们的初衷：整个过程中就是在博弈。产生器尽可能伪造出真实的数据，而判别器尽可能提高自身的判别性能。注意到我们刚刚构造的似然函数是针对判别器D(⋅)的优化目标函数。因此，我们一方面希望对判别器的可学习参数优化，极大化对数似然函数，另一方面我们希望对判别器的可学习参数优化，极小化对数似然函数。将此形式化得到我们的优化目标：