神经网络中product（乘积）层的作用

最近遇到一个在网络合并结构时是采用element-wise product，如图：

于是查了查product层在神经网路中的作用，可能是增强神经网络的特征交叉能力，类似于通过一个分支去辅助另一个分支。

原文链接：https://zhuanlan.zhihu.com/p/111842425

用MLP去做特征交叉还不是轻而易举。但细想起来并不是那么简单。

大家都非常清楚，感知机的结构是一个基于加法操作的结构（下图），两个特征从来没有直接交叉过。即使到了下一层，不同特征之间，也不会直接相乘，而是继续以加权和的方式叠加起来。

感知机的结构

那既然这样，为什么还说MLP具备特征交叉的能力呢？

就是因为激活函数的存在，为MLP提供了非线性能力。特征加权求和的结果，通过sigmoid，tanh这类激活函数之后，与其他神经元的输出进行进一步的混合，再通过下一层神经元的激活函数增加非线性，经过层层神经网络处理后，使MLP具备了特征交叉的能力，甚至在层数非常多之后，具备了拟合任意函数的能力。

但是，这里还是要强调的是，MLP这种特征交叉的能力是比较弱的，MLP不是天生为了进行特征交叉设计的。回到这篇文章标题中的话题，这也就是为什么很多深度学习神经网络加入product层（特征乘积层）的原因。

我们来回顾一下那些加入了product层的知名的深度学习网络。

Google的Wide&Deep模型中，Wide部分其实是两个特征的乘积层。

Google Wide Deep

DeepFM中，用FM layer进行特征交叉，用MLP进行作为DeepFM中的Deep部分。

DeepFM

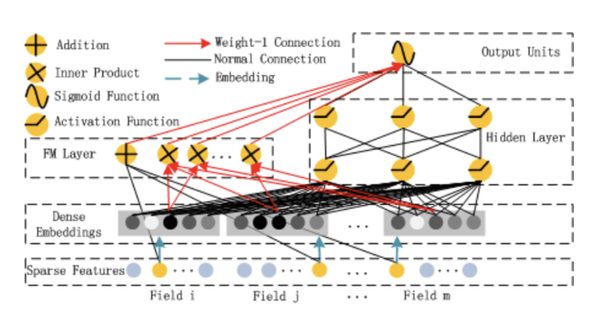
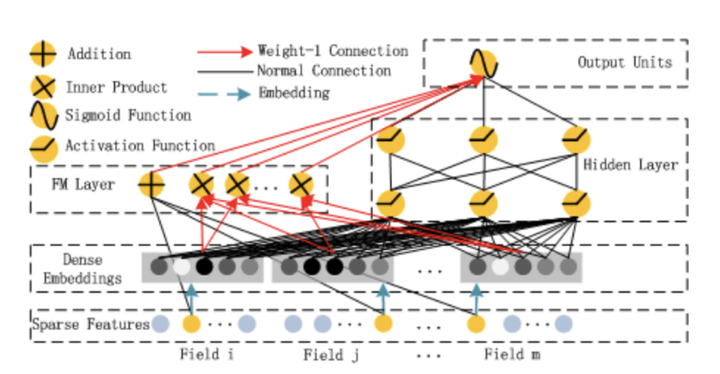
PNN中则是直接加入了Product Layer，加强特征交叉能力。

PNN

当然专门针对特征交叉进行改造的模型还有很多，诸如Deep Crossing，Deep&Cross等。这些网络有的直接通过乘积操作将两个特征相乘，有的通过FM这类善于处理特征交叉的模型作为特征交叉层，有的通过构造一些特征cross的方法进行特征组合。但所有这些都充分说明了一点，仅仅采用MLP进行特征组合的能力是不够的，需要有针对性的在模型中加入特征交叉的结构。

总结

今天跟大家讨论了一个有意思的知识点——MLP的特征组合能力。我的结论是MLP理论上具备特征交叉和特征组合的能力，但在神经网络层数较浅时，特征交叉的能力较弱，于是在实践中，往往会在深度学习网络中加入特征交叉的结构来提高特征交叉的效率。