拉普拉斯变换笔记（2）

拉普拉斯变换的收敛域(ROC)与逆变换(ILT)

1.是否可积即是否收敛(如果可收敛,面积/拉氏值即为收敛域)

（1）收敛的条件：e^(-jwt)积分为振荡函数

 （2）常系数线性微分方程对应线性时不变系统，其分析步骤有三：

 （3）拉氏逆变换（ILT）的方法：

传递函数的极点：s=-4,s=-1;

求解过程中令s=-4,s=-1解出A,B；

---

传递函数(Transfer Function)与拉普拉斯变换

传递函数

以水的流入作为输入，以水箱的高度作为输出，通过对该模型的微分方程进行拉普拉斯变换，我们可以得到 \((s+g/R)X(s)=U(s)\) 这样的方程，经过移项我们可以得到系统输出与输入的比值，而这个比值的表达式就是这个系统的传递函数

二端口网络输入和输出之间会存在某种数学关系，这个关系就是所谓的传递函数，也是这个二端口网络的数学模型G(s)。

特别注意，G(s)在表现形式上和F(s)一样，都是关于s的函数，但其物理意义不一样：F(s)表示信号的数值变化规律，G(s)表示的是传递网络输入输出信号之间的数学计算关系，即输入信号是通过怎样的运算过程（数乘、积分、微分等）得到输出信号的。

---

稳定性分析

当为0时，我们可以认为这个点为平衡点

 

 A为不稳定，B为临界稳定，始终有界，没有衰减，C为稳定点，最终衰减为零

如果输入有界，输出也为有界，称为BIBO稳定（如果一个系统在一个有界输入或扰动作用下其响应是有限的。），此处B、C都为皆为此。

稳定性分析

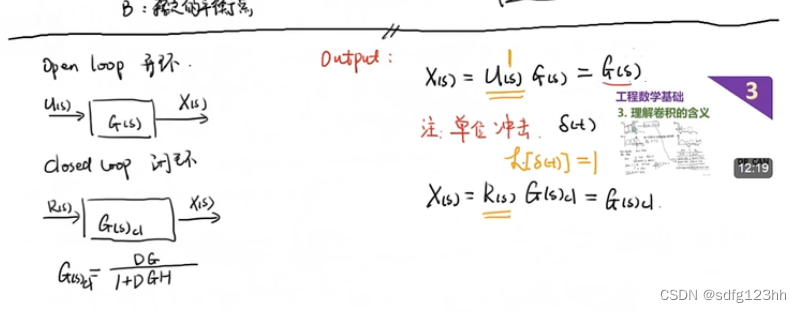
1、首先应该明确分析对象，

2、给系统输入一个单位冲击（相当于输入），单位冲击是宽度为0，面积为1的理想函数。其拉式变换为1，其系统输出为G(s)。

3、研究开环或者闭环的传递函数G(s)本身就可以分析稳定性。