各种norm的理解

0-norm 非零元素的个数

应用,比如要想找出不重叠的数据, 那么表示数据的向量应该尽量正交, 而正交呢就是向量相乘应该为0, 也就是让非零元素的个数尽量少, 所以可以min 0-norm去设计优化函数, 0-norm一般不能解,通常会用1-norm去解

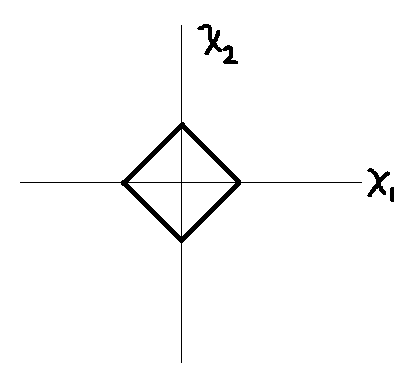
1-norm是元素绝对值相加, 以二维来讲

所以优化的时候会优化到棱形的四个点上, 所以1-norm的优化结果就是大的有值,  小的没值, 

应用: 找出数据中的突变的数据

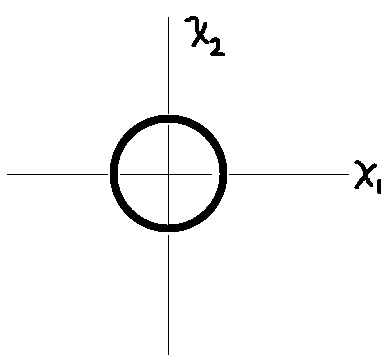
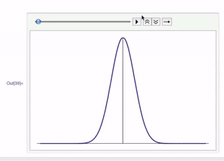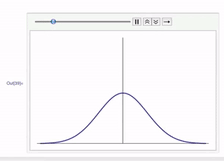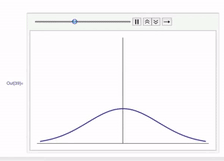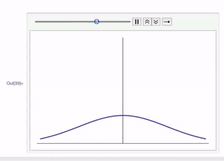
2-norm的图像是个圆

所以它优化的结果就是使点落在圆上, 当然圆上每个点的概率会一样,所以它的结果就会使元素上都有值, 使元素平滑, 就像热传导方程一样

而1norm就是使曲线变尖, 在值大的地方突出, 在值小的地方为0

对于Mesh来说, 每个点就是一维, 允许点上有大值存在, 就是假设它是outliers

核范数*

核范数的结果就是矩阵的秩, 

应用:矩阵补全,为了使矩阵空间之间的列之间更有关联性,就要使矩阵的秩尽量减小, 那么这个时候就需要他的秩尽量减小,这时就可以minimize矩阵的秩

2,1-norm

2,1-norm ,对于矩阵, 先每列列内平滑, 然后列间找出突出值

应用: 用在视频中的找出场景切换

1.2-norm , 相反先找出每列的突出值, 然后在列间平滑

2-norm称为lasso

2,1-norm称为group lasso

1,2-norm 称为exclusive group lasso