自控：梅森公式总是数错，怎么破？

一、梅森公式

对于用信号流图表示的控制系统，可以用梅森（ Mason）公式方便地求出从输入信号到输出信号的传递函数。为了给出梅森公式的表达式，先给出如下几个定义。
（1）前向通道：从输入到输出的一条按箭头方向可以走通并且在每个节点只通过一次的通道
（2）回路：从某个节点出发按箭头方向回到该节点并且在每个节点只通过一次的通道。
（3）不接触回路：若两个回路没有公共节点，则称它们为不接触回路。
梅森公式可以表示如下：
$$G(s)=\frac{1}{△(s)}\sum _i{Q}_i(s){△}_i(s)$$
式中，$G(s)$表示从某个输入信号到某个输出信号的传递函数。表达式右边各项的意义如下：
$$\begin{array}{rl}△(s)=& 1－所有不同回路的传递函数之和\\ & ＋每两个不接触回路的传递函数乘积之和\\ & －每三个不接触回路的传递函数乘积之和\\ & ＋\dots \\ & －\dots \end{array}$$
（即：加偶减奇）

$Q_i(s)$——从该输入到该输出的某前向通道的传递函数。
${△}_i(s)$——将$△(s)$中与$Q_i(s)$通道接触的回路的传递函数令为零后得到的表达式。
$△(s)$——称为系统的特征式。

二、例题

求如图所示系统的传递函数：

为了方便后面的表示，找到每个节点，标上字母：

2.1 前向通道怎么数

根据前向通道的定义，只要不回头，把所有可能性都考虑到即可。上面的信号流图，其实可以用图论的方法来分析，由于R到a和e到C是固定的，因此目标就是找到从a到e的所有符合条件的路径。首先建立各个节点之间的邻接矩阵：第$(i,j)$个元素表示从第$i$个节点到第$j$个节点的传递函数。

	a	b	c	d	e
a		G2	G6
b	-G10		G3		G7
c				G4
d			-G8		G5
e	-G9

接下来我们从R出发，首先到达a，然后观察到a的出度是2，可以到b也可以到c，因此分两种情况：
1）R-a-b
站在b这个点继续走，由于“前向通道不回头”，因此，从b出发的下一步只能是c、d、e，不可能再回到已经去过的a了。从邻接矩阵上看，可选的就是c或者e了。因此，这里再分两种情况：
1-1）R-a-b-c
到达c以后，由于“前向通道不回头”，因此，下一步只能是d、e，不可能再回到已经去过的a、b了。从邻接矩阵上看，可选的就是d了。从d再出发，路径为R-a-b-c-d，因此下一步只能是e，不可能再回到已经去过的a、b、c了。最后，再从e到C，整条路径为R-a-b-c-d-e-C。
1-2）R-a-b-e
从e出来以后，直接到C，因此整条路径为R-a-b-e-C。
2）R-a-c
到达c以后，由于“前向通道不回头”，因此，下一步只能是b、d、e，不可能再回到已经去过的a了。从邻接矩阵上看，可选的就是d了。与1-1类似，得到整条路径为R-a-c-d-e-C。

整理一下，我们找到的3条前向通道，用节点顺序表示为：
（1）R-a-b-c-d-e-C
（2）R-a-b-e-C
（3）R-a-c-d-e-C

其实，这个过程可以视为一棵树的构造，从a往下推到e，一旦路上出现重复的节点，就排除：

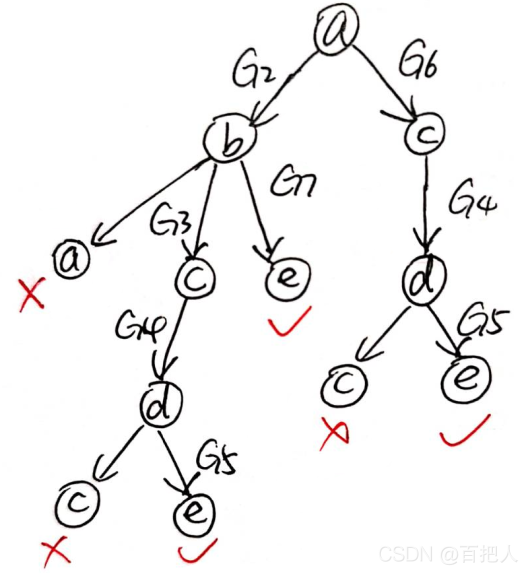
然后再以两两节点为端点，在邻接矩阵上找它们之间的传递函数，把整条路经上的传递函数串联即可：
$Q_1(s)=G_1(s)G_2(s)G_3(s)G_4(s)G_5(s)$
$Q_2(s)=G_1(s)G_2(s)G_7(s)$
$Q_3(s)=G_1(s)G_6(s)G_4(s)G_5(s)$

2.2 回路怎么数

回路，根据定义，从哪里出发，就要回到哪里。和2.1类似，也可以通过构造树来求解，只不过这次不是从a到e，而是从a到a、从b到b、从c到c、从d到d、从e到e——所谓“回路”。同时，也必须保证除了起点和终点相同以外，没有其他节点是重复访问的。

1）从a到a
根据邻接矩阵可以看出，要想回到a，整条路径的倒数第二个节点必须是b或者e（表上第1列），这可以帮助我们在画树的时候有所预判。

找到的回路有：
（1）a-b-a
（2）a-b-c-d-e-a
（3）a-b-e-a
（4）a-c-d-e-a
对应的传递函数为：
$L_1(s)=-G_2(s)G_{10}(s)$
$L_2(s)=-G_2(s)G_3(s)G_4(s)G_5(s)G_9(s)$
$L_3(s)=-G_2(s)G_7(s)G_9(s)$
$L_4(s)=-G_4(s)G_5(s)G_6(s)G_9(s)$

2）从b到b

找到的回路有：
（1）b-a-b
（2）b-c-d-e-a-b
（3）b-e-a-b
可以发现，这里的三条回路全部和“从a到a”的前三条回路重复了，也就是说上面辛苦画了图，结果却白找了。怎么避免这种白费力的情况呢？观察这里的第一条回路b-a-b，它其实是一个包含了a和b两个节点的环，既然是一个环，那么它也可以写成a-b-a，这也就是“从a到a”的第一条回路。因此，在找“从b到b”的回路的时候，我们应该排除掉所有出现a的线路——因为凡是经过a的环，必然也属于“从a到a”的回路，是前面已经找过的。

3）从c到c
有了前面的经验，我们在找“从c到c”的回路时，需要排除所有会出现a和b的线路。由于最后需要回到c，因此从邻接矩阵来看，回路里经过的倒数第二个节点必然是a, b, d其中之一，又因为我们需要排除a和b，所以从c到c的回路必然是c-…-d-c的形式。

可以看到，由于我们排除了a和b，因此这次搜索的规模一下子减小了。找到的回路为：c-d-c，对应的传递函数为：$L_5(s)=-G_4(s)G_8(s)$

4）从d到d
同理，从d到d的回路中不应该出现a, b, c；而从邻接矩阵可以看到，只有经过c才能到达d，因此不存在符合条件的“从d到d”的回路。

5）从e到e
同理，从e到e的回路中不应该出现a, b, c, d；由于e是最后一个节点，它没法不经过其他节点而到达自己，因此，也不存在符合条件的“从e到e”的回路。

终于数完了！
总结一下，我们找到的回路有5条：
（1）a-b-a
（2）a-b-c-d-e-a
（3）a-b-e-a
（4）a-c-d-e-a
（5）c-d-c
对应的传递函数为：
$L_1(s)=-G_2(s)G_{10}(s)$
$L_2(s)=-G_2(s)G_3(s)G_4(s)G_5(s)G_9(s)$
$L_3(s)=-G_2(s)G_7(s)G_9(s)$
$L_4(s)=-G_6(s)G_4(s)G_5(s)G_9(s)$
$L_5(s)=-G_4(s)G_8(s)$
从数的过程来看，一开始“从a到a”的回路是最多的，后面“从x到x”的回路由于要规避前面已经出现过的节点，因此新增的回路会很少，搜索的速度会变快。

2.3 找不接触回路，求系统特征式

回顾一下不接触回路的定义：若两个回路没有公共节点，则称它们为不接触回路。
也就是说，对于上面找到的5条回路，我们要一一对照着看。
例如对于（1）a-b-a，和它配对的不接触回路肯定不经过a和b，观察（2）（3）（4）（5），发现（5）c-d-c是符合要求的。
对于（2）a-b-c-d-e-a，不存在和它配对的不接触回路。
对于（3）a-b-e-a，（5）c-d-c是符合要求的。
对于（4）a-c-d-e-a，不存在和它配对的不接触回路。
对于（5）c-d-c，（1）a-b-a和（3）a-b-e-a是符合要求的，但是前面已经找过了，重复的不算。

找不接触回路的时候，也有两个省力的方法：

• 为了避免重复，找（1）的不接触回路的时候，备选是（2）（3）（4）（5）；找（2）的不接触回路的时候，就不考虑（1）了，只看（3）（4）（5）是否满足；以此类推。
• 一共只有abcde五个节点，一个回路至少有2个节点，所以任何一条包含5个节点的回路都不存在跟它匹配的不接触回路。

结论：$L_1(s)$和$L_5(s)$、$L_3(s)$和$L_5(s)$是不接触回路。

2.4 ${△}_i(s)$

由于$L_1(s)$和$L_5(s)$、$L_3(s)$和$L_5(s)$是不接触回路，因此系统的特征式为：
$$\begin{array}{rl}△(s)& =1-\sum _{i=1}^5{L}_i+L_1{L}_5+L_3{L}_5\\ & =1+G_2{G}_{10}+G_2{G}_3{G}_4{G}_5{G}_9+G_2{G}_7{G}_9\\ & +G_6{G}_4{G}_5{G}_9+G_4{G}_8+G_2{G}_{10}{G}_4{G}_8+G_2{G}_7{G}_9{G}_4{G}_8\end{array}$$
接下来算${△}_i(s)$，回顾一下定义：
$Q_i(s)$——从该输入到该输出的某前向通道的传递函数。
${△}_i(s)$——将$△(s)$中与$Q_i(s)$通道接触的回路的传递函数令为零后得到的表达式。
我们前面找到的前向通道为：
（1）R-a-b-c-d-e-C
（2）R-a-b-e-C
（3）R-a-c-d-e-C
计算的$Q_i(s)$为：
$Q_1(s)=G_1(s)G_2(s)G_3(s)G_4(s)G_5(s)$
$Q_2(s)=G_1(s)G_2(s)G_7(s)$
$Q_3(s)=G_1(s)G_6(s)G_4(s)G_5(s)$

因此，计算${△}_1(s)$需要令$△(s)$中与$Q_1(s)$通道接触的回路的传递函数令为零，也就是让经过a-b-c-d-e中任意节点的$L_i=0$，显然所有$L_i$都经过a-b-c-d-e，因此所有$L_i=0$，${△}_1(s)=1$。
计算${△}_2(s)$需要令$△(s)$中与$Q_2(s)$通道接触的回路的传递函数令为零，也就是让经过a-b-e中任意节点的$L_i=0$，这时候只有$L_5\ne 0$，因此${△}_2(s)=1-L_5=1+G_4{G}_8$。
计算${△}_3(s)$需要令$△(s)$中与$Q_3(s)$通道接触的回路的传递函数令为零，也就是让经过a-c-d-e中任意节点的$L_i=0$，显然所有$L_i$都经过a-c-d-e，因此所有$L_i=0$，${△}_3(s)=1$。

2.5 结果表示

综上，可以得到系统传递函数为：
$$\begin{array}{rl}G(s)& =\frac{C(s)}{R(s)}=\frac{Q_1(s)\ast 1+Q_2(s)\ast (1+G_4{G}_8)+Q_3(s)\ast 1}{△(s)}\\ & =\frac{G_1{G}_2{G}_3{G}_4{G}_5+G_1{G}_2{G}_7(1+G_4{G}_8)+G_1{G}_6{G}_4{G}_5}{1+G_2{G}_{10}+G_2{G}_3{G}_4{G}_5{G}_9+G_2{G}_7{G}_9+G_6{G}_4{G}_5{G}_9+G_4{G}_8+G_2{G}_{10}{G}_4{G}_8+G_2{G}_7{G}_9{G}_4{G}_8}\end{array}$$

参考资料

[1]田玉平，蒋珉，李世华．自动控制原理[M]．北京：科学出版社，2006