线性代数之行列式偏导

                            线性代数之行列式偏导

矩阵偏导

针对y或者f(x)是元素，x是矩阵的情况，则元素对矩阵的求导形式如下：

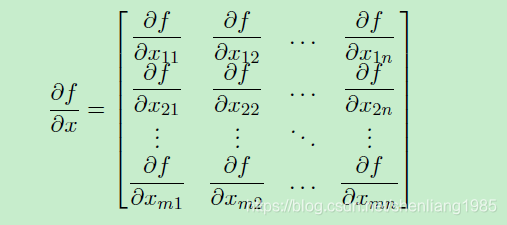
注:这里的 ​ 和矩阵x是同型（行数列数相同）的。

行列式性质

这里假定A是方阵，则有如下性质：

1 余子式是将行列式的第i行、第j列删除后组成的新行列式，一般用如下符号表示：

比较一般的例子(M11)见：

2 对余子式求余因子，则称为代数余子式。表达式为：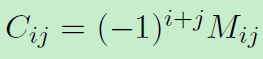

3 行列式的值等于某一行(列)的各个元素与其对应的代数余子式的乘积之和，即  

4由行列式A的代数余子式Aij 的转置所构成的矩阵叫做伴随矩阵，其定义如下：

即可简写为： ，其中C为代数余子式。

5 对于非奇异（行列式不为0）的矩阵A，有如下性质：

这里由伴随矩阵的定义得： ，因为A可逆，则容易得上式(即中间式子右乘A-1)。

注：这里的A*即是 。

行列式偏导

因为行列式是标量函数，所以之前关于标量函数的定义与性质都适应于行列式。

按照行列式分量展开的形式看，则有：

针对整个行列式，则有:

注：1 这里借助矩阵导数的概念：

2 伴随矩阵等于代数余子式矩阵的转置

行列式偏导与矩阵逆

接行列式偏导的定义，针对行列式A是非奇异(行列式不为0)的情况，则可以进一步转换：

1 将伴随矩阵转换为行列式和矩阵逆的乘积  

2 再结合常数乘矩阵逆的性质，即可将常数提到外面，最终得