【AI 大模型】RAG 检索增强生成 ④ ( 向量相似度计算 | 余弦距离 | 欧式距离 | OpenAI 文本向量模型 | 手动实现的 余弦相似度 和 欧氏距离 函数计算 )

上一篇博客 【AI 大模型】RAG 检索增强生成 ③ ( 文本向量 | Word2Vec 词汇映射向量空间模型 - 算法原理、训练步骤、应用场景、实现细节 | Python 代码示例 ) 中 , 简单展示了 文本向量 的生成过程 和 表现形式 , 本篇博客中介绍 如何使用这些 文本向量 ;

一、向量相似度计算

---

向量相似度计算 : 在 自然语言处理 ( NLP ) 和 机器学习 中 , 文本向量 相似度计算 是衡量两个文本语义相似性的核心任务 ;

常用的两种距离度量方法是

• 余弦距离 ( Cosine Distance ) : 基于 向量夹角 的 余弦值 衡量相似性 ;
• 欧氏距离 ( Euclidean Distance ) : 在 n 维向量空间 中两点之间的直线距离 ;

二者各有优缺点和适用场景 ;

场景	余弦距离	欧氏距离
文本相似度	✔️ 更适合（高维稀疏，方向敏感）	❌ 不适用（长度影响大）
推荐系统	✔️ 更适合（用户兴趣方向）	❌ 不适用（活跃度影响大）
高维稀疏数据	✔️ 更适合（忽略零值维度）	❌ 不适用（受噪声维度干扰）
图像处理	❌ 不适用（像素值长度有意义）	✔️ 更适合（绝对差异重要）
物理空间距离	❌ 不适用（需要绝对距离）	✔️ 更适合（直接反映距离）
低维稠密数据	❌ 不适用（方向可能不显著）	✔️ 更适合（全局差异重要）
异常检测	❌ 不适用（需要绝对差异）	✔️ 更适合（衡量偏差）

二、余弦距离

---

1、余弦距离 概念

余弦距离 ( Cosine Distance ) 是 基于 向量夹角 的 余弦值 衡量相似性 ;

• 余弦相似度计算 : 余弦相似度 取值范围 [ -1 , 1 ] ;

$$\mathrm{CosineSimilarity}=\frac{\mathrm{X}\cdot \mathrm{Y}}{\Vert X\Vert \Vert Y\Vert }$$

• 余弦距离计算 : 余弦距离 取值范围 [ 0 , 2 ] ;

$$\mathrm{CosineDistance}=1-\mathrm{CosineSimilarity}$$

公式截图 : 防止 Latext 代码失效 ; ( Markdown 中的 Latext 代码仅在 CSDN 生效 )

上述公式中的 X 和 Y 各自都是一个向量空间中的向量 ;

• $X=(x_1,x_2,\cdots ,x_n)$ 是 第一个向量点 , 每个向量的分量 如 $x_1,x_2,\cdots ,x_n$ 各自都是一个浮点值 ;
• $Y=(y_1,y_2,\cdots ,y_n)$ 是 第二个向量点 , 每个向量的分量 如 $y_1,y_2,\cdots ,y_n$ 各自都是一个浮点值 ;

公式中的

$$\mathrm{X}\cdot \mathrm{Y}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}}$$

是两个向量 $\mathrm{X}=({\mathrm{x}}_1,{\mathrm{x}}_2,\cdots ,{\mathrm{x}}_{\mathrm{n}})$ 和 $\mathrm{Y}=({\mathrm{y}}_1,{\mathrm{y}}_2,\cdots ,{\mathrm{y}}_{\mathrm{n}})$ 的 点积 ;

上述 X 和 Y 向量可参考如下值 , 每个向量都有 50 个浮点值确定 , 则这两个向量点就是 50 维向量空间中的点 ;

 Vector: [-0.00321157  0.03927787  0.00616916  0.02789649  0.02203173  0.03612738
  0.00637109  0.04316046 -0.049891    0.02915843 -0.00426264  0.02841807
  0.01823073  0.0149862  -0.02141328 -0.00687046  0.0535442   0.01235065
 -0.046329    0.00192757 -0.00424403  0.00364727  0.05790862  0.04215468
  0.04061833  0.03017248 -0.03808379  0.05979197  0.03251123 -0.01618787
 -0.05283526 -0.01509981  0.05030754 -0.03224825  0.05769876 -0.01519872
  0.02141866  0.01543435 -0.01191425 -0.00674526  0.00728445  0.04265702
  0.01254657  0.04424815 -0.05862596 -0.00738266  0.01891772  0.02471734
  0.01362135  0.02899224]

这是上一篇博客 【AI 大模型】RAG 检索增强生成 ③ ( 文本向量 | Word2Vec 词汇映射向量空间模型 - 算法原理、训练步骤、应用场景、实现细节 | Python 代码示例 ) 中 使用 tensorflow 中提供的 Word2Vec 模型 提取的 文本向量 ;

2、余弦距离 特点

余弦距离 特点 : 该类型距离 方向敏感 , 长度不敏感 , 仅关注向量的方向差异 , 忽略向量的大小 ( 模长 ) ;

余弦距离 示例 : 给出两个句子

• “ 我喜欢机器学习 ”
• “ 我热爱深度学习 ”

获取两个句子的 文本向量 , 这两个句子的方向接近 ,

但是 由于 词频差异 导致 长度可能不同 ,

其 余弦相似度 高 , 余弦距离 近 , 欧式距离 远 ;

3、余弦距离 适用场景

余弦距离 适用场景 : 余弦距离 通过 计算向量夹角的余弦值 来衡量相似性 , 关注向量的方向而非长度 ;

• 文本相似度计算 : 文本向量 通常是 高维稀疏的 , 如 : TF-IDF、词袋模型、BERT Embedding , 余弦距离能有效捕捉语义方向 ;
  • 搜索引擎 : 查询 关键字 与 文档内容 的相似性 ;
  • 问答系统 : 匹配 用户问题 与 候选答案 ;
  • 文本聚类 : 将 语义相似 的文本进行聚类分组 ;
• 推荐系统 : 用户 兴趣向量 的 方向 比 长度 更能反映 用户的个人偏好 ;
• 高维稀疏数据 : 高维数据中 非零维度较少 , 余弦距离 能有效忽略零值维度的影响 ;
• 向量长度不一致 : 向量长度差异较大 但 方向相似 时 , 余弦距离更合适 ;
  • 长短文本比较 : 长文本与短文本的相似性比较 ;
  • 用户活跃度不同但兴趣相似 ;

4、余弦距离 代码示例

代码示例 :

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity

# 定义两个向量
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# 计算余弦相似度
cos_sim = cosine_similarity([A], [B])[0][0]  # 输出: Cosine Similarity: 0.9746318461970762
print("Cosine Similarity:", cos_sim)

# 计算余弦距离
cos_distance = 1 - cos_sim  # 输出: Cosine Distance: 0.025368153802923787
print("Cosine Distance:", cos_distance)

执行结果 :

Cosine Similarity: 0.9746318461970762
Cosine Distance: 0.025368153802923787

三、欧式距离

---

1、欧式距离 概念

欧氏距离 ( Euclidean Distance ) 是 在 n 维向量空间 中两点之间的直线距离 , 公式如下 :

$$\mathrm{EuclideanDistance}=\mathrm{d}(\mathrm{X},\mathrm{Y})=\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{x}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}\right)}^2}$$

公式截图 : 防止 Latext 代码失效 ;

上述公式中的

• $\mathrm{X}=({\mathrm{x}}_1,{\mathrm{x}}_2,\cdots ,{\mathrm{x}}_{\mathrm{n}})$ 是 第一个向量点 , 每个向量的分量 如 $x_1,x_2,\cdots ,x_n$ 各自都是一个浮点值 ;
• $\mathrm{Y}=({\mathrm{y}}_1,{\mathrm{y}}_2,\cdots ,{\mathrm{y}}_{\mathrm{n}})$ 是 第二个向量点 , 每个向量的分量 如 $y_1,y_2,\cdots ,y_n$ 各自都是一个浮点值 ;

欧氏距离 的 值是 非负数 , 值越小表示越相似 ;

2、欧式距离 特点

欧氏距离 特点 :

• 对 绝对距离 敏感 , 同时考虑了 两个向量 的 方向和大小差异 ;
• 对 向量归一化 敏感 , 如果向量未归一化 , 词频高 的 长文本 的 欧氏距离 会天然大于 短文本 , 可能掩盖语义相似性 ;
• 欧氏距离 不适用于 高维稀疏文本向量 , 欧氏距离 容易受噪声维度影响 ;

3、欧式距离 适用场景

欧式距离 适用场景 : 欧氏距离通过 计算向量空间中两点的直线距离来衡量相似性 , 同时关注向量的方向和长度 ;

• 物理空间距离计算 : 欧氏距离 直接反映 向量空间 中 两点之间的绝对距离 ;
  • 地理位置 : 计算两个地点之间的距离 ;
  • 传感器数据差异计算 : 测量设备之间的物理差异 ;
• 图像处理 : 图像 像素值 向量的 长度和方向 都有意义 ;
  • 图像相似度计算 : 计算两幅图像的像素值差异 ;
  • 图像检索 : 基于内容的图像搜索 ;
• 低维稠密数据 : 在低维数据中 , 所有维度都有意义 , 欧氏距离能捕捉全局差异 ;
  • 物理实验数据对比 : 如温度、压力等测量值 ;
  • 金融数据对比 : 如股票价格的时间序列 ;
• 需要绝对差异度量的场景 : 欧氏距离更合适 需要绝对差异度量的场景 ;
  • 异常检测 : 检测与正常样本的偏差 ;
  • 聚类分析 : 基于绝对距离的分组 ;

4、欧式距离 代码示例

代码示例 :

import numpy as np
from sklearn.metrics.pairwise import euclidean_distances

# 定义两个向量
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# 计算欧氏距离
euclidean_dist = euclidean_distances([A], [B])[0][0]  # 输出: Euclidean Distance: 5.196152422706632
print("Euclidean Distance:", euclidean_dist)

执行结果 :

Euclidean Distance: 5.196152422706632

四、OpenAI 文本向量模型

---

1、OpenAI 的 text-embedding-ada-002 文本向量模型

text-embedding-ada-002 是 OpenAI 发布的 文本嵌入 ( Embedding ) 模型 , 属于第二代嵌入模型系列 ;

• 核心功能 : 将文本（单词、句子、段落）转换为高维向量（Embedding）, 捕捉文本的语义信息 ;
• 输出维度 : 生成 1536 维的浮点数向量 ;
• 适用场景 : 语义搜索、文本相似度计算、聚类分析、分类任务等 ;

text-embedding-ada-002 适合快速构建语义相关的应用 , 如 : 搜索、推荐 ;

虽然存在领域和语言限制 , 但其低成本、易用性和高性能使其成为大多数场景的首选工具 ;

对于复杂需求 , 可结合本地模型或领域数据进行补充优化 ;

text-embedding-ada-002 模型 代码示例 : 下面代码的 api_key , 替换你自己的 api_key 和 接口 , 代码中的 api_key 删除了 ;

from openai import OpenAI

# 生成文本向量
# 这里替换你自己的 api_key 和 接口, 这里的 api_key 隐藏了
client = OpenAI(api_key="sk-i3dHq7757aF6", base_url="https://api.xiaoai.plus/v1")

# text-embedding-ada-002 模型是 OpenAI 提供的
def get_embedding(texts, model="text-embedding-ada-002"):
    '''封装 OpenAI 的 Embedding 模型接口'''
    data = client.embeddings.create(input=texts, model=model).data
    return [x.embedding for x in data]

# 计算相似度
text1 = "测试文本转向量"

# 计算出 文本向量
vec1 = get_embedding(text1)

# 打印文本向量
print(vec1)

执行结果如下 : 输出了 1536 个浮点数 , 就不在这里完整的贴出来了 ;

[[-0.009152066893875599, -0.008041816763579845, -0.00519117247313261, 0.014065677300095558, 0.0068490467965602875, 0.022430066019296646, -0.017283903434872627 ... ]]

2、使用 Scikit-learn 机器学习库中的函数计算文本向量距离

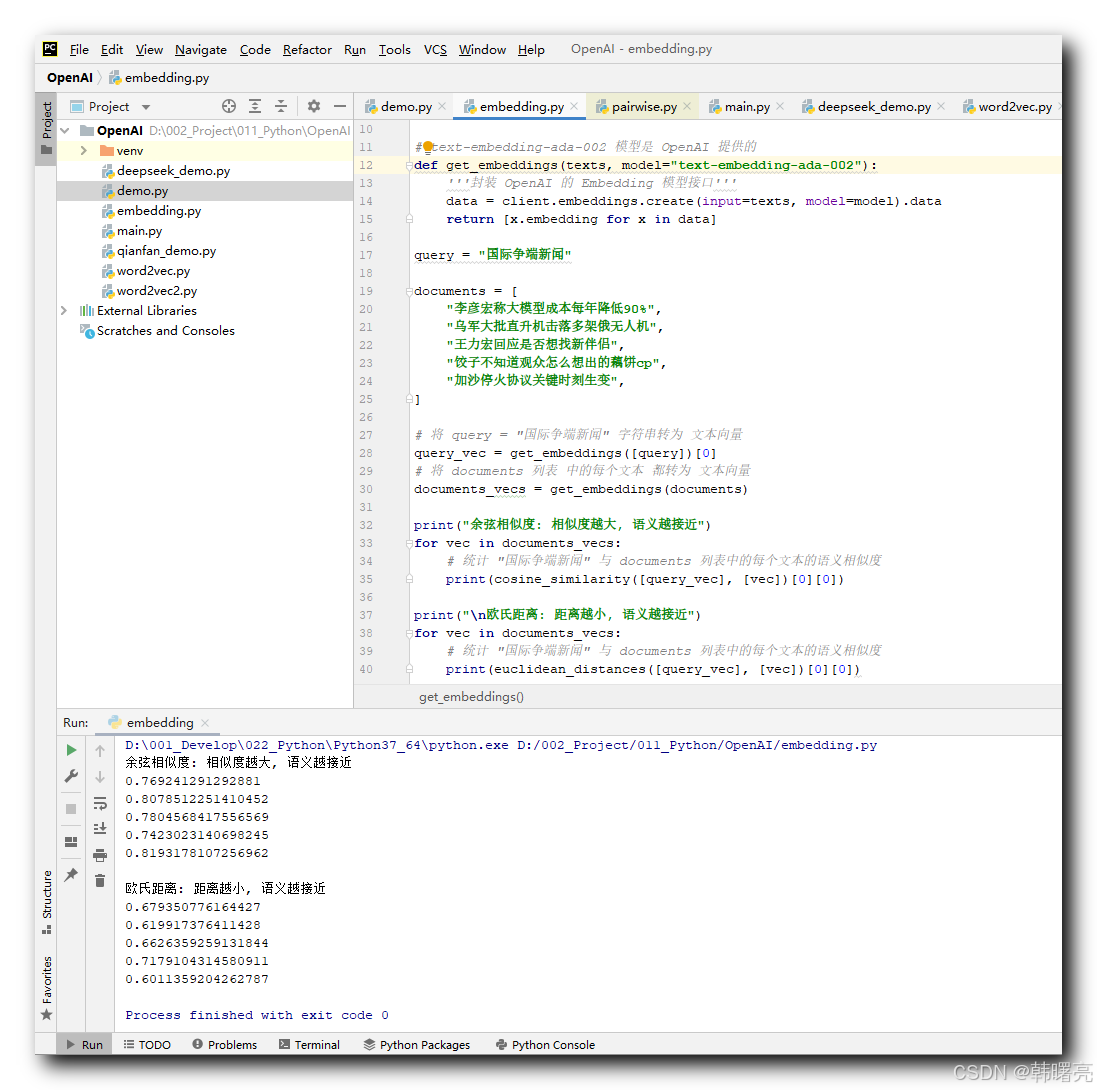
下面这段代码的主要功能是使用 OpenAI 的 text-embedding-ada-002 模型将文本转换为向量 , 并计算 Scikit-learn 机器学习库中的 余弦相似度 和 欧氏距离 函数 衡量查询文本与一组文档的语义相似性 ;

代码示例 : 下面代码的 api_key , 替换你自己的 api_key 和 接口 , 代码中的 api_key 删除了 ;

import numpy as np
from numpy import dot
from numpy.linalg import norm
from openai import OpenAI
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.metrics.pairwise import cosine_similarity

# 这里替换你自己的 api_key 和 接口, 这里的 api_key 隐藏了
client = OpenAI(api_key="sk-i3dHqZ7757aF6", base_url="https://api.xiaoai.plus/v1")

# text-embedding-ada-002 模型是 OpenAI 提供的
def get_embeddings(texts, model="text-embedding-ada-002"):
    '''封装 OpenAI 的 Embedding 模型接口'''
    data = client.embeddings.create(input=texts, model=model).data
    return [x.embedding for x in data]

query = "国际争端新闻"

documents = [
    "李彦宏称大模型成本每年降低90%",
    "乌军大批直升机击落多架俄无人机",
    "王力宏回应是否想找新伴侣",
    "饺子不知道观众怎么想出的藕饼cp",
    "加沙停火协议关键时刻生变",
]

# 将 query = "国际争端新闻" 字符串转为 文本向量
query_vec = get_embeddings([query])[0]

# 将 documents 列表 中的每个文本 都转为 文本向量
documents_vecs = get_embeddings(documents)

print("余弦相似度: 相似度越大, 语义越接近")
for vec in documents_vecs:
    # 统计 "国际争端新闻" 与 documents 列表中的每个文本的语义相似度
    print(cosine_similarity([query_vec], [vec])[0][0])

print("\n欧氏距离: 距离越小, 语义越接近")
for vec in documents_vecs:
    # 统计 "国际争端新闻" 与 documents 列表中的每个文本的语义相似度
    print(euclidean_distances([query_vec], [vec])[0][0])

执行结果 :

余弦相似度: 相似度越大, 语义越接近
0.769241291292881
0.8078512251410452
0.7804568417556569
0.7423023140698245
0.8193178107256962

欧氏距离: 距离越小, 语义越接近
0.679350776164427
0.619917376411428
0.6626359259131844
0.7179104314580911
0.6011359204262787

五、手动实现的 余弦相似度 和 欧氏距离 函数计算

---

1、余弦距离计算

代码示例 :

• 首先 , 计算两个向量的点积 np.dot(a, b)

• 然后 , 计算每个向量的 L2 范数 , 也就是 模长 np.linalg.norm

• 再后 , 计算余弦相似度 , 点积除以两个向量模长的乘积

• 最后 , 计算 余弦距离：1 - 余弦相似度 ;

# 导入 numpy 库，用于数学计算
import numpy as np

# 定义余弦距离函数
def cosine_distance(a, b):
    """
    计算两个向量之间的余弦距离。

    参数:
    a (numpy.ndarray): 第一个向量。
    b (numpy.ndarray): 第二个向量。

    返回:
    float: 余弦距离，范围在 [0, 2] 之间。
    """
    # 计算向量 a 和向量 b 的点积（内积）
    dot_product = np.dot(a, b)

    # 计算向量 a 的 L2 范数（模长）
    norm_a = np.linalg.norm(a)

    # 计算向量 b 的 L2 范数（模长）
    norm_b = np.linalg.norm(b)

    # 计算余弦相似度：点积除以两个向量模长的乘积
    cos_sim = dot_product / (norm_a * norm_b)

    # 余弦距离 = 1 - 余弦相似度
    return 1 - cos_sim


# 示例向量
A = np.array([1, 2, 3])  # 向量 A
B = np.array([4, 5, 6])  # 向量 B

# 计算向量 A 和向量 B 之间的余弦距离
cos_dist = cosine_distance(A, B)  # 输出: 0.026

# 打印余弦距离结果
# Cosine Distance : 0.025368153802923787
print("Cosine Distance :", cos_dist)

执行结果 :

Cosine Distance : 0.025368153802923787

2、欧式距离计算

np.linalg.norm(a - b) 代码 是 计算的是L2 范数 ;

L2 范数（也叫 欧几里得范数，Euclidean Norm）是 向量的长度或模长，表示从原点到该点的欧几里得距离。

$$\Vert X{\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

3 维向量 $X=(3,4,12)$ 的 L2 范数计算 :

$$\Vert X{\Vert }_2=\sqrt{3^2+4^2+12^2}=\sqrt{169}=13$$

代码示例 :

# 导入 numpy 库，用于数学计算
import numpy as np

def euclidean_distance(a, b):
    """
    计算两个向量 a 和 b 之间的欧氏距离。

    参数：
    a -- 第一个向量（NumPy数组）
    b -- 第二个向量（NumPy数组）

    返回：
    两个向量之间的欧氏距离（标量值）
    """
    return np.linalg.norm(a - b)  # 使用 NumPy 的范数函数计算欧氏距离

# 示例向量
A = np.array([1, 2, 3])  # 向量 A
B = np.array([4, 5, 6])  # 向量 B

# 计算向量 A 和向量 B 之间的欧氏距离
ecul_dist = euclidean_distance(A, B)  # 输出: 0.026

# 打印余弦距离结果
# Euclidean Distance : 5.196152422706632
print("Euclidean Distance :", ecul_dist)

执行结果 :

Euclidean Distance : 5.196152422706632