提要
转行搞科研之后,发现最重要的是数学和物理。
偏导,方导,梯度,散度,旋度是高等数学的几个基本概念,在图形学中会经常用到,这里重新来学习一下,同时也当作一个记录。
偏导
定义:一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
数学表示:函数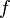
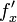
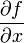
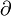
由定义可求得:
几何含义:偏导数f'x(x0,y0)表示固定面上一点对x轴的切线斜率;偏导数f'y(x0,y0)表示固定面上一点对y轴的切线斜率。
例子:求 z=x^2+3xy+y^2 在P(1,2)处的偏导数。
解: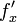

将(1,2)带入得


方向导数
定义:方向导数(Directional derivative)是一个多变量可微函数上的任意一点沿着某一向量方向的瞬时变化率。偏导数是沿坐标轴方向的变化率,方向导数是偏导数的概念的推广。
数学描述:设函数 z = f(x,y) 在点 p(x,y) 的某一邻域内有定义.自点 P 引射线 l ,


梯度
定义:标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
数学描述:在二维情况下,设函数 z=f(x,y),在平面区域D内具有一阶连续偏导数,则对于D内某个点P,可以确定一个向量
多维情况依次扩展。
假设有一个房间,房间内所有点的温度由一个标量场\phi给出的,即点(x,y,z)的温度是\phi(x,y,z)。假设温度不随时间改变。然后,在房间的每一点,该点的梯度将显示变热最快的方向。梯度的大小将表示在该方向上变热的速度。
考虑一座高度在(x, y)点是H(x, y)的山。H这一点的梯度是在该点坡度(或者说斜度)最陡的方向。梯度的大小告诉我们坡度到底有多陡。
和方导的关系:梯度的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
散度
定义:散度描述的是向量场里一个点是汇聚点还是发源点,形象地说,就是这包含这一点的一个微小体元中的向量是“向外”居多还是“向内”居多。散度是个标量。
数学描述:设有一个向量场
一个区域内的通量为:
则有散度:
引入Nabda算子:
则有:
物理意义:对流体来说,散度指流体运动时单位体积的改变率。就是流体的形状虽然改变,但是由于散度为0,则其面积或体积不变。散度等于零的区域称为无源场或管形场。流体力学中,散度为零的流体称为不可压缩流体,也就是说此流体中不会有一部分凭空消失或突然产生。
旋度
定义:表示三维向量场对某一点附近的微元造成的旋转程度。 这个向量提供了向量场在这一点的旋转性质。旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴,它和向量旋转的方向满足右手定则。旋度向量的大小则是绕着这个旋转轴旋转的环量与旋转路径围成的面元的面积之比。
数学描述:在向量场A中,由环量的定义得场A在某一点的旋度为:
引入Nebda算子,旋度可表示为:
物理含义:旋度是曲线、向量场旋转的程度。矢量的旋度是环流面密度的最大值,与面元的取向有关。
参考
wikipedia
百度百科








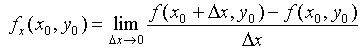
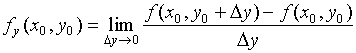



























 1889
1889

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








