从今开始就真正走进三维动画的世界,完全一个菜鸟级别的,只能够一点一点前进了。前些时看了一些关于三维重建的文献,记录点看的相关的知识,备以后查看吧!
按照虚拟场景的构造方法来区分,目前有三种主要的建模方法:基于几何的建模与渲染方法(GBMR)、基于图像建模与渲染方法(IBMR)及基于几何与图像混合建模与渲染的方法。
(1)基于几何建模与渲染又称为基于图形建模与渲染,首先对实际场景中所有的物体进行抽象,用多边形构造虚拟景观的三维几何模型,并建立虚拟环境中的光照和材质模型。然后进行纹理映射及控制参数设定,利用透视投影原理将三维几何模型变换到二维屏幕空间,经过裁减、阴暗处理、隐藏面消除等处理生成一个屏幕投影,在输出设备上实时渲染出视景画面,从而完成对整个场景的漫游。
(2)基于图像建模与渲染技术(IBMR)分为两部分,基于图像的建模(IBM)和基于图像的渲染(IBR)。基于图像的建模有很大的局限性。而基于图像渲染技术是利用摄像机采集的离散图像或摄像机采集的连续视频作为基础数据,经过图象处理生成真实的全景图像,然后通过合适的空间模型把多幅全景图像组织为虚拟实景空间,用户在这个空间中可以前进、后退、环视、仰视、俯视、近看、远看等操作。
(3)基于几何与图像的混合建模与渲染技术,是先利用IBMR构造虚拟场景的环境来获得逼真的视觉效果,同时对虚拟环境中用户要与之交互的对象利用GBMR来进行实体构建,这样既增加了场景真实感,又能保证实时性与交互性。混合建模虽然具有各种优点,但其实现也带来了很多技术上的困难。
依据所含几何信息的多少可将IBR方法分为3大类。
(1)不含几何的渲染:全光函数的渲染,全景图拼接,中心圆拼接,光场渲染。
(2)内含几何的渲染:视图插值,视图变形,Lumigraph,表面光场(SLF)。
(3)几何与图像的混合渲染:三维图形变形,分层深度图像渲染,纹理映射模型。
光场渲染技术(LFR),其内容是在不需要图像的深度信息或相关性的条件下,通过预先拍摄的一组场景照片,建立该场景的光场数据库,然后对于任意给定的新视点,经过重采样和双线性插值运算,得到该视点的视图,实现对整个场景的漫游。
基于图像渲染方法研究
IBR技术的理论基础研究
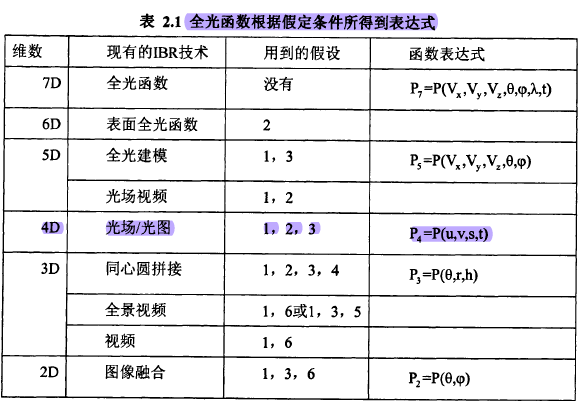
IBR技术的理论基础是Adelson等人提出的全光函数(Plenoptic Function)。以一个针孔摄像机模拟人眼,假设在时刻t时针孔摄像机处于空间坐标P=P(Vx,Vy,Vz)位置,从以球坐标系标定的方向V=V(Θ,Φ)上摄入摄像机的光线波长为λ,则这束光线可表示为P7=Plenoptic(Vx,Vy,Vz,Θ,Φ,λ,t),这就是完整的全光函数,它是一个七维函数,函数值为该束光线的辐射度(Radiance)。
当使用图像进行三维场景渲染即IBR时,对IBR定义如下:给定用于描述某个场景的连续全光函数,则基于图像的渲染技术是一个采样一渲染的两阶段过程。采样
阶段从全光函数获取用于存储和显示用的采样信息。渲染阶段使用获取到的采样信息重构出一个连续全光函数。
对全光函数的假设条件分析
1)当使用图像作为采样的保存结果时,光波长范围被减少到(红绿蓝)三个通道:
2)空气是透明的,当穿过不包含阻挡物的区域时,光线将保持固定的强度;
3)若场景维持静态的状态,则时间维可以忽略;
4)若限定观察者(视点)的活动范围至一个平面,则可将全光函数降低一个维度;
5)若限定观察者(视点)的活动范围至某一条直线,则可将全光函数降低两个维度;
6)若观察者(视点)固定,则可将全光函数降低三个维度。
























 3737
3737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








