Attention Is All You Need学习笔记

Attention Is All You Need学习笔记

这个笔记是对2017年Google在发表的《Attention Is All You Need》一些笔记。笔记按照文章的结构来做的。
文章PDF地址：https://arxiv.org/abs/1706.03762

(一) 引言

• RNN(如LSTM, GRU)在序列建模和转换问题(如语言建模和机器翻译), 被认为是最先进的方法.
• RNN模型在计算上是顺序执行的, 时间片 t 的计算依赖t-1时刻的计算结果, 这种机制阻碍了训练过程的并行化, 训练的代价高。
• 使用注意力机制，即使当序列在输入和输出的位置上偏离的比较远, 也一样可以对这些序列的依赖关系进行建模(即注意力机制可以实现对长期依赖进行建模).

(二）背景

• 要降低前面所说的序列计算代价，也可以使用卷积神经网络的方法, 如Extended Neural GPU, ByteNet 以及ConvS2S, 但即便是这些模型, 也是比较难以对长距离的依赖信息进行建模的, 因为它们的计算代价与距离呈线性关系/对数线性关系.
• 论文提出的Transformer中, 这些计算可以降低至常量级别, 虽然由于对用attention权重化的位置取平均降低了效果，但是使用Multi-Head Attention可以对此进行抵消.
• Self-attention机制，它关联单个序列的不同位置以计算序列的表示。

(三) 模型的架构

3.1 Encoder and Decoder Stacks

1. 模型的总体架构如下图所示:
   
2. Encoder和Decoder中, 分别使用6个完全一致层来处理, 这里使用6个，完全是作者自己定义的，完成可以改为其它的数量, 结构如下图所示:
   
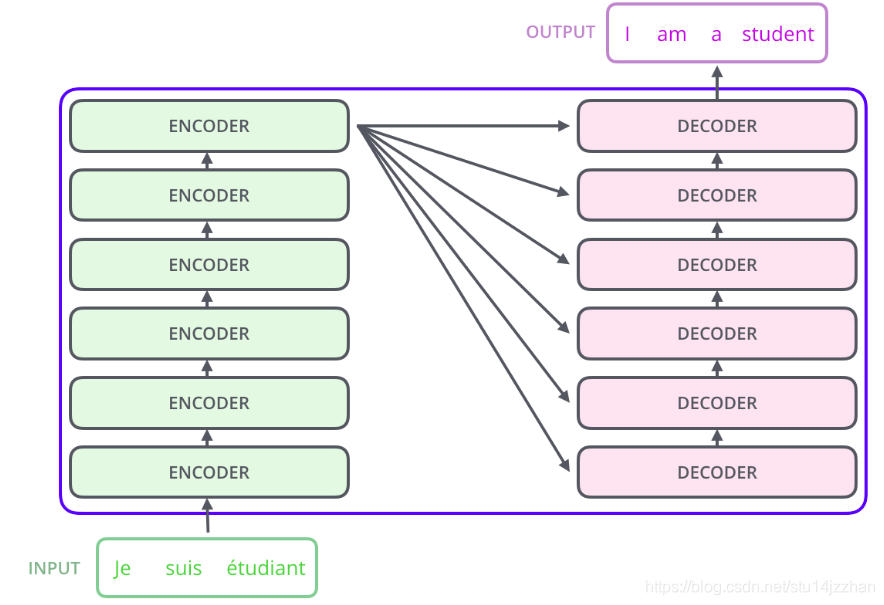
3. 在Encoder部分, 每个Encoder层由两个子层构成: 多头的自注意机制(multi-head self-attention mechanism) 和 全连接的前馈神经网络(position-wise fully connected feed-forward network)构成. 同时使用参差及层标准化来连接这两个子层, 即$LayerNorm(x+sublayer(x))$, 这里使用用参差连接的原因待会再作解释.
4. Decoder部分除了Encoder中的两个子层外， 还增加了一个子层, 用来Encoder中的输出施加multi-head attention. 同时, 也对自注意机制做了一些调整，避免在前面位置的时候Attention到接下来的位置.

3.2 Attention

1. 注意力机制可以描述: 从一堆key-value的集合中, 对某个query进行查询, 这里的key, value, query都是向量. 这个过程, 使用通俗的话来描述的话, 就是你有一个query, 你从一堆的key-value的集体中, 通过query和key进行某种意义上的相似度计算, 我们的输出就是value的加权平均, 而权重又是根据相似度计算得来的。

2. 论文使用的注意力机制的公式为
   $$Attention(Q;K;V)=softmax(\frac{K{Q}^T}{\sqrt{d_k}})V$$这里的softmax函数, 其实是起到了将各个权重进行了处理, 使其和为1的作用, 同时, 分子中的$\sqrt{d_k}$是为了避免维度过大, 对结果造成影响. 试想下, 如果维度比较大, 那$K{Q}^T$的值的尺度(magnitude)就会比较大, 那么当再经过softmax函数后, 将会导致对应的梯度过小.

3. 多头注意力机制
   前面所阐述的是一个注意力机制. 我们完全可以使用一个长维度(记为$d_{model}$)的注意力机制, 但如果我们使用多个短的维度(记为$d_v$)的注意力机制似乎会好。一方面, 它可以并行计算; 另一方面, 它可以像CNN的特征层一样, 每个注意力机制去学习不同的注意力(即注意不同的信息), 这种方式比单一的一个注意力机制能提取更多的信息, 且更高效也更稳定. 这多个注意力将会以下图的方式进行处理, 在下图中， 8个注意力的结果$Z_1...Z_8$拼接成一个长的矩阵$Z_1:Z_8$, 然后再乘以一个$W^O$矩阵, 从而得到结果矩阵$Z$
   

4. 在Decoder中的第2子层“encoder-decoder attention”, 查询前面子层的decoder layer产生的查询向量$q$时, 我们所使用Key-Value向量是来自Encoder中最终的输出. 使用这种方式，可以模拟传统的Encoder-Decoder机制.

5. 论文提出的自注意力机制与其它的注意力机制有什么区别呢?
   传统的注意力机制, 使用的是 输入与输出之间的注意力，即在输出的过程中，对输入有不同的侧重. 而自注意力机制，它所考察的是, 输入序列中的symbol与其它的symbols之间的关系.

6. 在解码的过程中, 自注意力机制在解码当前位置时, 会同时注意到输出序列前后的位置，这个对破坏auto-regressive的特性，我们需要让它只注意到输出序列前面的位置, 对于不合理的位置, 论文会进行mask(具体的, 是在softmax前, 对部分位置的值置为-Inf.

3.3 Position-wise Feed-Forward Networks

1. 全连接网络使用ReLU激活函数(使用了两次线性变换)$$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$$
2. 这个过程也可以使用两个1x1的卷积核来实现

3.4 Embeddings and Softmax

1. 根据前面层得到的结果，再使用线性变换及Softmax函数, 就可以得到每个词对应的概率了, 取出概率最大的词, 就是当前位置预测的结果了

3.5 Positional Encoding

1. 自注意力机制并不能捕捉序列的顺序，即如果将句子的顺序都打乱, 根据自注意力机制, 依然可以得到相同的结果. 而句子的位置信息对于机器翻译问题来说是相当重要的，因此有必要对位置信息进行编码, 在模型中把这一信息给体现出来.
2. 论文给出的方式为:
   $$P{E}_{(pos,2i)}=\sin \left(pos/10000^{2i/d_{\text{ model }}}\right)$$
   $$P{E}_{(pos,2i+1)}=\cos \left(\mathrm{pos}/10000^{2i/d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}\right)$$
   这里, $pos$为位置, 而$i$为维度.
3. Position Embedding本身是一个绝对位置的信息，但在语言中，相对位置也很重要，Google选择前述的位置向量公式的一个重要原因是：由于我们有$sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta$以及$cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta$，这表明位置p+k的向量可以表示成位置p的向量的线性变换，这提供了表达相对位置信息的可能性。
4. 这里解释前面所提到的在Encoder和Decoder中都使用参差连接的作用: Residuals carry positional information to higher layers, among other information. 无论是Encoder还是Decoder, 都是使用了多层， 如果没有使用Residuals的方式的话, 在高层Layer中将会遗失位置信息.

4. Why Self-Attention

1. 之所以引入自注意机制, 主要有3个方面的原因:

• 每一层的计算复杂度
• 计算的并行度
• 学习长期记忆的难易程度
  下面的表格给出了这三个方面的对比
  

2. 这里给出一个注意力层计算的复杂度计算:
   我们记$n$为序列的长度, $d$为表示层的长度, 即$d_k$与$d_v$, 由前面的公式$Attention(Q;K;V)=softmax(\frac{K{Q}^T}{\sqrt{d_k}})V$中, 我们知道$Q\in {\mathbb{R}}^{\mathbf{n}\times d_k},K\in {\mathbb{R}}^{m\times d_k},V\in {\mathbb{R}}^{m\times d_v}$. 这里$K{Q}^T$所需要的计算复杂度为$O(n^{2}d)$, 而剩余的部分, $softmax$函数及scale部分, 都只是$O(n)$, 至于最后一部的矩阵乘法, 时间复杂度也为$O(n^{2}d)$, 因此, 注意力层的时间复杂度为$O(n^{2}d)$
3. 论文还给出了一个restricted版本的自注意力机制, 它是只考虑相邻的$r$个邻居, 通过这样的方式, 可以将计算复杂度减低到$O(rnd)$

参考

苏剑林. (2018, Jan 06). 《《Attention is All You Need》浅读（简介+代码） 》[Blog post]. Retrieved from https://kexue.fm/archives/4765