4.3 分段低次插值

 

 

学习目标：

如果我要学习分段低次插值，我可能会采取以下几个步骤：

1. 学习插值的基本概念和方法

在学习分段低次插值之前，我需要先掌握插值的基本概念和方法，例如拉格朗日插值、牛顿插值和内维尔方法等。这些基础知识可以帮助我理解分段低次插值的原理和实现方法。

1. 学习分段低次插值的原理和方法

在学习分段低次插值之前，我需要了解分段函数的概念和性质。然后，我可以学习分段低次插值的原理和方法，例如分段线性插值和分段三次 Hermite 插值等。我需要理解每种方法的实现原理、优缺点以及适用范围。

1. 理解分段低次插值的实现细节和计算方法

在掌握了分段低次插值的基本原理之后，我需要深入了解每种方法的实现细节和计算方法。例如，我需要理解如何将原始数据拆分成多个小区间，以及如何在每个小区间内进行插值计算。我还需要掌握如何计算分段插值多项式的系数，并学会使用程序实现这些计算。

1. 练习分段低次插值的应用和实现

最后，我需要通过练习来加强自己对分段低次插值的掌握。我可以寻找一些实际应用场景，并尝试使用分段低次插值方法对数据进行插值计算。同时，我还可以使用各种数学软件或编程语言实现分段插值的计算，并通过实际操作来加深自己对这些方法的理解和掌握程度。

 

4.3.1 分段线性插值与分段二次插值

分段插值是一种将数据拆分成多个小区间，然后在每个小区间内进行插值计算的方法。分段插值可以更好地逼近非光滑函数，并且具有较高的计算效率和稳定性。其中，分段线性插值和分段二次插值是常见的分段插值方法，下面分别进行讲解：

1. 分段线性插值

分段线性插值是一种使用线性函数逼近数据的插值方法。它将整个数据集拆分成多个小区间，然后在每个小区间内使用线性函数逼近数据。假设要在区间 [x_i, x_{i+1}]内进行插值计算，那么可以使用以下线性函数：

 

其中，f_i和 f_{i+1} 分别是区间 [x_i, x_{i+1}]内的两个数据点的函数值。这个公式可以理解为在区间内使用一条直线逼近数据。

1. 分段二次插值

分段二次插值是一种使用二次函数逼近数据的插值方法。它将整个数据集拆分成多个小区间，然后在每个小区间内使用二次函数逼近数据。假设要在区间 $[x_i, x_{i+1}]$ 内进行插值计算，那么可以使用以下二次函数：

 

其中，a_i、b_i 和 c_i是待求系数。为了求解这些系数，需要使用区间内的三个数据点 (x_i,f_i)、(x_{i+1},f_{i+1})和 (x_{i+2},f_{i+2})，并假设在 x_i 和 x_{i+2}处的导数值相等，即：

 

然后，再使用插值条件 f(x_i)=f_i 和 f(x_{i+1})=f_{i+1}，以及 x=x_i 和 x=x_{i+1}两个点的导数值相等，即：

 

解出 a_i

 我的理解：

分段插值是一种将给定数据在不同区间内采用不同的插值多项式进行插值的方法。在分段插值中，将数据分为若干个子区间，每个子区间内使用一个低次插值多项式进行插值，从而得到整个数据的插值函数。

分段线性插值是一种分段插值的方法，它使用线性函数在每个子区间内进行插值。具体来说，对于一组给定的数据 (x_i, y_i)，分段线性插值将数据分为 n个子区间，每个子区间 (x_{i-1}, x_i)用一条直线连接 (x_{i-1}, y_{i-1})和 (x_i, y_i)进行插值，从而得到整个数据的插值函数。

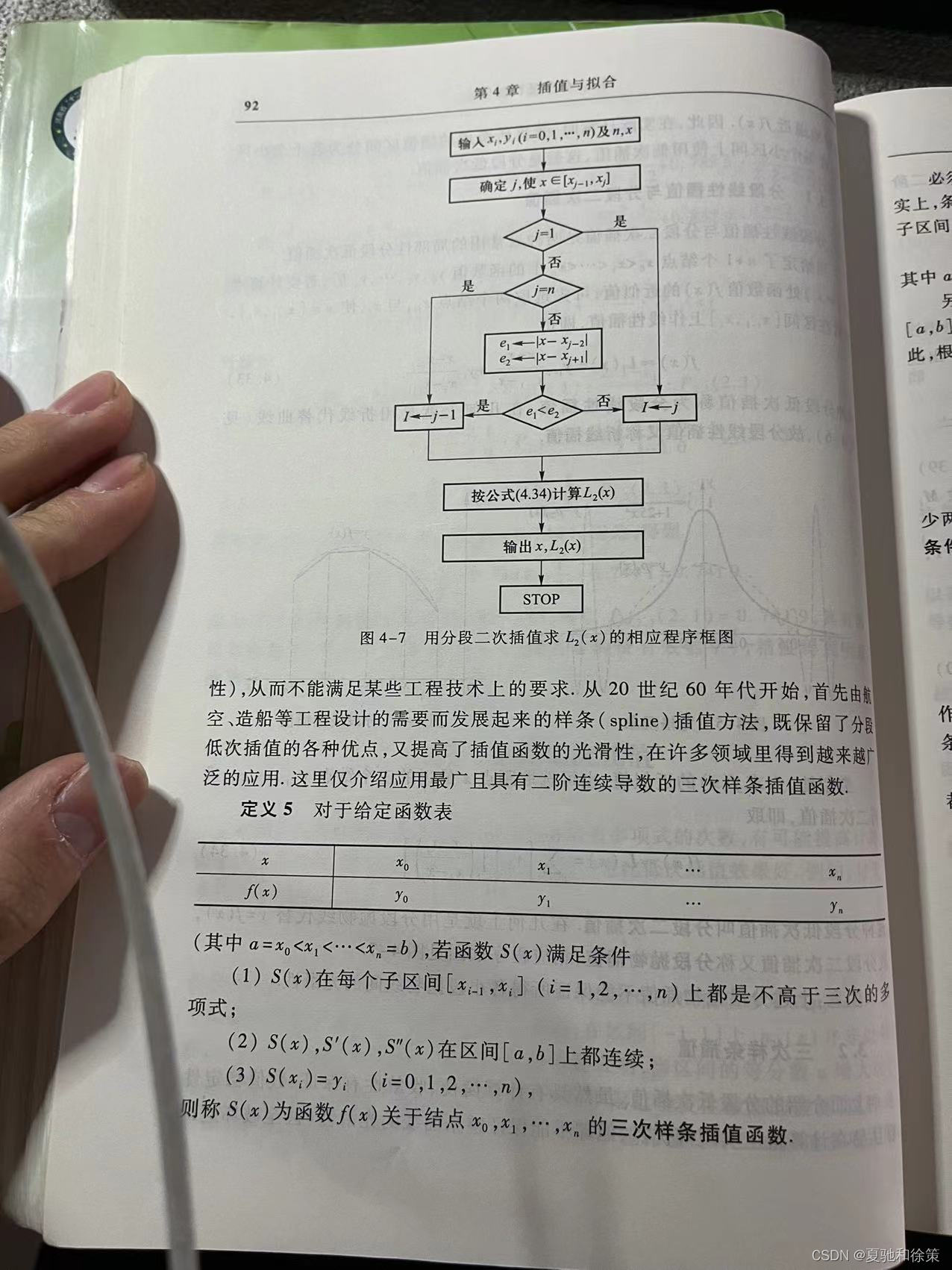
分段二次插值是一种分段插值的方法，它使用二次函数在每个子区间内进行插值。具体来说，对于一组给定的数据 (x_i, y_i)，分段二次插值将数据分为 n个子区间，每个子区间 (x_{i-1}, x_i)用一个二次函数连接 (x_{i-1}, y_{i-1})、(x_i, y_i)和 (x_{i+1}, y_{i+1})进行插值，从而得到整个数据的插值函数。

在分段插值中，关键是如何确定子区间的边界以及在每个子区间内使用何种插值函数进行插值。此外，还需要考虑插值函数的光滑性和精度问题，以及如何避免插值函数的震荡现象。在实际应用中，需要根据具体问题的特点和需求选择合适的分段插值方法，并进行适当的优化和调整。

 4.3.2 三次样条插值

三次样条插值是一种分段插值的方法，它使用三次函数在每个子区间内进行插值，同时保证插值函数在子区间内是光滑的。具体来说，对于一组给定的数据 (x_i, y_i)，三次样条插值将数据分为 $n$ 个子区间，每个子区间 (x_{i-1}, x_i)用一个三次函数连接 (x_{i-1}, y_{i-1})、(x_i, y_i)和 (x_{i+1}, y_{i+1})进行插值，从而得到整个数据的插值函数。

三次样条插值的插值函数具有较高的光滑性和精度，同时也能够较好地避免插值函数的震荡现象。在三次样条插值中，使用的插值函数是一组三次多项式，因此需要在每个子区间内确定四个系数，共计 4n个系数。为了确保插值函数的光滑性，需要在子区间内使用连续的三次函数，并且需要满足一定的边界条件，如自然边界条件或固定边界条件等。

三次样条插值的求解过程一般采用矩阵计算方法，需要先求解出一组三对角矩阵，并通过矩阵分解的方式求解插值函数的系数。由于三次样条插值的计算比较复杂，因此在实际应用中，需要对数据进行预处理和优化，以提高插值效率和精度。

 我的理解：

三次样条插值是一种基于多项式插值的分段插值方法，主要用于对一组给定的数据点进行平滑曲线的拟合，从而得到一个连续的函数。

具体来说，对于一组给定的数据点 (x_i, y_i)，三次样条插值将其分成若干个子区间，每个子区间内使用一个三次多项式进行插值，使得插值函数在子区间内具有二阶连续可导性，也就是说，插值函数在子区间内的一阶导数和二阶导数都是连续的。

这种插值方法主要是为了解决分段函数拟合问题，通过构造一个分段的三次多项式来逼近数据点，使得插值函数不仅能够平滑地穿过所有数据点，还能够避免插值函数在过渡区域出现明显的振荡现象。

三次样条插值的计算方法主要包括三个步骤：首先需要确定每个子区间内的三次多项式系数；然后需要确定边界条件，如自然边界条件或固定边界条件等；最后，利用矩阵计算的方法求解插值函数的系数。

三次样条插值具有较高的精度和光滑性，常用于数据拟合、图像处理、数值积分等领域。但需要注意的是，在某些特殊情况下，三次样条插值可能会导致过拟合或者欠拟合现象，因此在实际应用中需要根据具体情况选择合适的插值方法。

 

 4.3.3 三次样条插值函数性质

三次样条插值函数的主要性质包括：

1. 光滑性：三次样条插值函数在插值节点处具有一阶和二阶连续导数，插值函数曲线呈现出“平滑”的特点。
2. 唯一性：在给定的插值节点条件下，三次样条插值函数是唯一的。
3. 局部性：三次样条插值函数的计算仅依赖于相邻的两个节点，因此它是一种局部性的插值方法。
4. 拟合性：三次样条插值函数在整个插值区间内拟合数据的误差较小，因此具有较高的拟合精度。
5. 自由度：三次样条插值函数的自由度比分段低次插值高，可以通过引入边界条件等方式调整插值函数的自由度。
6. 计算复杂度：三次样条插值函数的计算复杂度较高，需要解线性方程组才能求解插值系数。

在使用三次样条插值函数时，需要注意插值节点的选择、边界条件的设置以及插值函数的求解方法等问题。同时，由于三次样条插值函数具有较高的拟合精度和光滑性，在实际应用中也需要考虑插值函数的计算效率和存储空间等问题。

 我的理解：

不同的插值方法都有各自的性质和特点。对于三次样条插值函数，这些性质可以帮助我们更好地理解和使用这种插值方法。

1. 光滑性：三次样条插值函数在插值节点处具有一阶和二阶连续导数，这意味着插值函数曲线在节点处呈现出“平滑”的特点，没有出现尖锐的转折或不连续的情况。这对于一些需要连续变化的实际问题，比如曲线拟合、数值微分和积分等方面非常有用。

2. 唯一性：在给定的插值节点条件下，三次样条插值函数是唯一的。这意味着，在确定插值节点的情况下，可以通过求解线性方程组得到唯一的插值函数。

3. 局部性：三次样条插值函数的计算仅依赖于相邻的两个节点，因此它是一种局部性的插值方法。这种局部性质使得三次样条插值方法可以在大规模数据集上进行高效的插值计算。

4. 拟合性：三次样条插值函数在整个插值区间内拟合数据的误差较小，因此具有较高的拟合精度。这是因为三次样条插值函数采用了更高阶的多项式函数来拟合数据，使得插值函数能够更准确地反映数据的变化趋势。

5. 自由度：三次样条插值函数的自由度比分段低次插值高，可以通过引入边界条件等方式调整插值函数的自由度。这种自由度的调节方式可以使得三次样条插值函数更加灵活，适应不同的插值问题。

6. 计算复杂度：三次样条插值函数的计算复杂度较高，需要解线性方程组才能求解插值系数。这使得三次样条插值方法在大规模数据集上的计算效率相对较低，需要针对具体问题进行优化。

 

 

 

 

 总结：

分段低次插值是一种将数据点分段用低次多项式连接起来的插值方法，其重点和难点在于如何选择合适的插值函数和区间划分方式，以及如何处理边界条件。

具体来说，分段低次插值的重点和难点包括：

1. 插值函数的选择：分段低次插值通常使用一次或二次多项式进行插值，因此需要根据实际数据的特点来选择合适的插值函数，避免过拟合或欠拟合现象的出现。

2. 区间划分的方式：区间划分是分段低次插值的核心之一，不同的划分方式会对插值结果产生影响，因此需要根据实际数据的特点来选择合适的划分方式。

3. 边界条件的处理：在分段低次插值中，边界条件通常包括自然边界条件、固定边界条件等。不同的边界条件会对插值结果产生影响，因此需要根据实际情况选择合适的边界条件。

4. 数值稳定性：在计算分段低次插值时，需要进行数值计算，如果计算不稳定会导致插值结果的不准确性。因此，需要注意数值计算中的精度控制和算法优化。

易错点包括：

1. 区间划分的不合理：如果区间划分不合理，会导致插值函数的过拟合或欠拟合现象。

2. 边界条件的选择不当：如果选择的边界条件不当，会导致插值函数的不连续或不光滑。

3. 数值计算的不稳定：如果数值计算不稳定，会导致插值结果的不准确性，甚至导致计算失败。

总之，分段低次插值是一种较为简单有效的插值方法，但需要根据具体问题选择合适的插值函数、区间划分方式和边界条件，并注意数值计算的稳定性。