12.7 傅里叶级数

12.7 傅里叶级数

第七节 傅里叶级数

从本节开始，我们讨论由三角函数组成的函数项级数，即所谓三角级数，着重研究如何把函数展开成三角级数。

---

一、三角级数与三角函数系的正交性

在第一章中，我们介绍过周期函数的概念，周期函数反映了客观世界中的周期运动。正弦函数是一种常见而简单的周期函数。例如描述简谐振动的函数：

这是一个以 2π2\pi2π 为周期的正弦函数，其中 yyy 表示动点的位置，ttt 表示时间，AAA 为振幅，aaa 为角频率，φ\varphiφ 为初相。

在实际问题中，除了正弦函数外，还会遇到非正弦函数的周期函数，它们反映了较复杂的周期运动。如电子技术中常用的周期为 TTT 的矩形波（图12-8），就是一个非正弦周期函数的例子。

如何研究非正弦周期函数？

联系到前面介绍过的用函数的幂级数展开式表示与讨论函数，我们也想将周期函数展开成由简单的周期函数例如三角函数组成的级数。具体地说，将周期为 TTT 的周期函数用一系列以 TTT 为周期的正弦函数 Ansin⁡(nat+φn)A_n \sin(nat + \varphi_n)An​sin(nat+φn​) 组成的级数来表示，记为：

其中 A0,An,φn(n=1,2,3,…)A_0, A_n, \varphi_n (n=1, 2, 3, \ldots)A0​,An​,φn​(n=1,2,3,…) 都是常数。

将周期函数按上述方式展开，它的物理意义是很明确的，这就是把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加。在电工学上，这种展开称为谐波分析，其中常数项 A0A_0A0​ 称为 f(t)f(t)f(t) 的直流分量，A1sin⁡(at+φ1)A_1 \sin(at + \varphi_1)A1​sin(at+φ1​) 称为一次谐波（又叫做基波），A2sin⁡(2at+φ2),A3sin⁡(3at+φ3),…A_2 \sin(2at + \varphi_2), A_3 \sin(3at + \varphi_3), \ldotsA2​sin(2at+φ2​),A3​sin(3at+φ3​),… 依次称为二次谐波，三次谐波，等等。

三角级数的标准形式

为了以后讨论方便起见，我们将正弦函数 Ansin⁡(nat+φn)A_n \sin(nat + \varphi_n)An​sin(nat+φn​) 按三角公式变形，得：

令 an=Ansin⁡φna_n = A_n \sin \varphi_nan​=An​sinφn​, bn=Ancos⁡φnb_n = A_n \cos \varphi_nbn​=An​cosφn​，并且令 ω=2πT(即T=2π)\omega = \frac{2\pi}{T} (即 T = 2\pi)ω=T2π​(即T=2π)，则公式(7-1)的右端可以改写为：

形如公式(7-2)的级数叫做三角级数，其中 a0,an,bn(n=1,2,3,…)a_0, a_n, b_n (n=1, 2, 3, \ldots)a0​,an​,bn​(n=1,2,3,…) 都是常数。

令 ω=1\omega = 1ω=1，T=2πT = 2\piT=2π，则公式(7-2)成为：

这就把以 2π2\pi2π 为周期的三角级数转换成以 2π2\pi2π 为周期的三角级数。

三角函数系的正交性

在区间 [−π,π][-π, π][−π,π] 上，三角函数系的正交性是指在三角函数系中的任何不同的两个函数的乘积在区间 [−π,π][-π, π][−π,π] 上的积分等于零，即：

这些等式都可以通过计算定积分来验证。现将第四式验证如下：

利用三角函数中的积化和差公式：

当 k≠nk \neq nk=n 时，有：

其余等式请读者自行验证。

相同函数的乘积积分

在三角函数系中，两个相同函数的乘积在区间 [−π,π][-π, π][−π,π] 上的积分不等于零，即：

这些等式为我们展开周期函数成傅里叶级数提供了重要的数学基础。

---

以上是傅里叶级数的基本概念和理论基础，接下来将继续深入探讨如何将具体的周期函数展开成傅里叶级数，并研究其收敛性和应用。

二、函数展开成傅里叶级数

设 f(x)f(x)f(x) 是周期为 2π2\pi2π 的周期函数，且能展开成三角级数：

我们自然要问：系数 a0,ak,bk,…a_0, a_k, b_k, \ldotsa0​,ak​,bk​,… 与函数 f(x)f(x)f(x) 之间存在着怎样的关系？换句话说，如何利用 f(x)f(x)f(x) 把 a0,ak,bk,…a_0, a_k, b_k, \ldotsa0​,ak​,bk​,… 表达出来？为此，我们进一步假设（7-5）式右端的级数可以逐项积分。

求 a0a_0a0​

对（7-5）式从 −π-\pi−π 到 π\piπ 积分，由于假设（7-5）式右端级数可逐项积分，因此有：

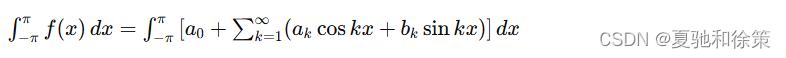
根据三角函数系的正交性，等式右端除第一项外，其余各项均为零，所以：

于是得：

求 aka_kak​

用 cos⁡nx\cos nxcosnx 乘（7-5）式两端，再从 −π-\pi−π 到 π\piπ 积分，我们得到：

根据三角函数系的正交性，等式右端除 k=nk = nk=n 的一项外，其余各项均为零，所以：

于是得：

求 bkb_kbk​

类似地，用 sin⁡nx\sin nxsinnx 乘（7-5）式的两端，再从 −π-\pi−π 到 π\piπ 积分，可得：

由于当 n=0n = 0n=0 时，a0a_0a0​ 的表达式正好给出 a0a_0a0​，因此，已得结果可以合并写成：

如果公式（7-6）中的积分都存在，这时它们定出的系数 a0,an,bn,…a_0, a_n, b_n, \ldotsa0​,an​,bn​,… 叫做函数 f(x)f(x)f(x) 的傅里叶 (Fourier) 系数。将这些系数代入（7-5）式右端，所得的三角级数：

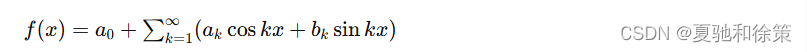
叫做函数 f(x)f(x)f(x) 的傅里叶级数。

傅里叶级数的收敛性

一个定义在 (−∞,∞)(-∞, ∞)(−∞,∞) 上周期为 2π2\pi2π 的函数 f(x)f(x)f(x)，如果它在一个周期上可积，那么一定可以作出 f(x)f(x)f(x) 的傅里叶级数。然而，函数 f(x)f(x)f(x) 的傅里叶级数是否一定收敛？如果它收敛，它是否一定收敛于函数 f(x)f(x)f(x)？

一般来说，这两个问题的答案都不是肯定的。那么 f(x)f(x)f(x) 在怎样的条件下，它的傅里叶级数不仅收敛，而且收敛于 f(x)f(x)f(x)？也就是说，f(x)f(x)f(x) 满足什么条件可以展开成傅里叶级数？这是我们面临的一个基本问题。

收敛定理

下面我们叙述一个收敛定理（不加证明），它给出关于上述问题的一个重要结论。

定理（收敛定理，狄利克雷 (Dirichlet) 充分条件）： 设 f(x)f(x)f(x) 是周期为 2π2π2π 的周期函数，如果它满足：

1. 在一个周期内连续或只有有限个第一类间断点，
2. 在一个周期内至多只有有限个极值点，

那么 f(x)f(x)f(x) 的傅里叶级数收敛，并且：

• 当 xxx 是 f(x)f(x)f(x) 的连续点时，级数收敛于 f(x)f(x)f(x)；
• 当 xxx 是 f(x)f(x)f(x) 的间断点时，级数收敛于：

收敛定理告诉我们：只要函数在 [−π,π][-π, π][−π,π] 上至多有有限个第一类间断点，并且不作无限次振动，函数的傅里叶级数在连续点处就收敛于该点的函数值，在间断点处收敛于该点左极限与右极限的算术平均值。可见，函数展开成傅里叶级数的条件比展开成幂级数的条件低得多。

记：

在 CCC 上成立 f(x)f(x)f(x) 的傅里叶级数展开式：

例题的博客：傅里叶级数展开与数学分析

例 1：周期函数的傅里叶级数展开

题目

设 f(x)f(x)f(x) 是周期为 2π2\pi2π 的周期函数，它在 (−π,π)(-\pi, \pi)(−π,π) 上的表达式为：

将 f(x)f(x)f(x) 展开成傅里叶级数，并作出级数的和函数的图形。

解答

所给函数 f(x)f(x)f(x) 满足傅里叶级数收敛定理的条件，在点 x=kπx = k\pix=kπ ( k=0,±1,±2,…k = 0, \pm 1, \pm 2, \ldotsk=0,±1,±2,… ) 处不连续，在其他点处连续。因此根据收敛定理，f(x)f(x)f(x) 的傅里叶级数收敛，并且当 x=kπx = k\pix=kπ 时级数收敛于

当 x≠kπx \neq k\pix=kπ 时级数收敛于 f(x)f(x)f(x)。

计算傅里叶系数如下：

1. 计算 a0a_0a0​:

1. 计算 ana_nan​:

由于 f(x)f(x)f(x) 是奇函数，且 cos⁡(nx)\cos(nx)cos(nx) 是偶函数，因此 f(x)cos⁡(nx)f(x) \cos(nx)f(x)cos(nx) 是奇函数，对称积分为零：

1. 计算 bnb_nbn​:

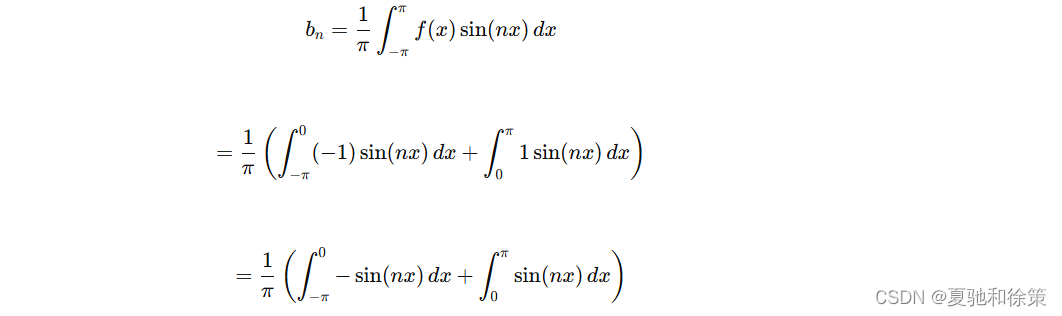
由对称性，可以将积分范围改为：

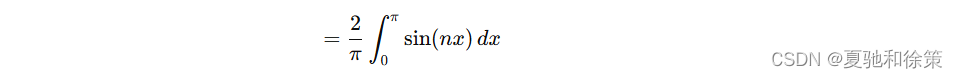
计算积分：

综上，f(x)f(x)f(x) 的傅里叶级数展开式为：

级数的和函数图形

根据上面的计算结果，画出傅里叶级数的和函数图形如下：


例 2：另一个周期函数的傅里叶级数展开

题目

设 f(x)f(x)f(x) 是周期为 2π2\pi2π 的周期函数，它在 [−π,π][-\pi, \pi][−π,π] 上的表达式为：

将 f(x)f(x)f(x) 展开成傅里叶级数，并作出级数的和函数的图形。

解答

所给函数 f(x)f(x)f(x) 满足收敛定理的条件，在点 x=(2k+1)πx = (2k+1)\pix=(2k+1)π ( k=0,±1,±2,…k = 0, \pm 1, \pm 2, \ldotsk=0,±1,±2,… ) 处不连续，因此傅里叶级数在这些点处收敛于：

在其他连续点 xxx 处收敛于 f(x)f(x)f(x)。

计算傅里叶系数如下：

1. 计算 a0a_0a0​:

1. 计算 ana_nan​:

由于 f(x)f(x)f(x) 是半周期函数，因此可以改为：

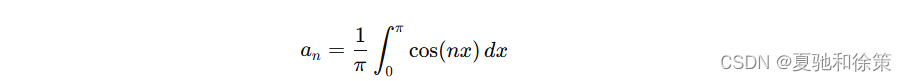
计算积分：

1. 计算 bnb_nbn​:

计算积分：

综上，f(x)f(x)f(x) 的傅里叶级数展开式为：

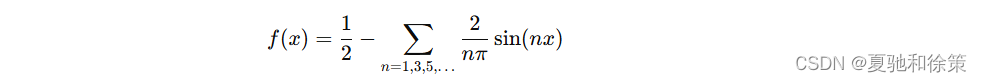
级数的和函数图形

根据上面的计算结果，画出傅里叶级数的和函数图形如下：


例 3：绝对值函数的傅里叶级数展开

题目

将函数 f(x)=E∣sin⁡(x)∣f(x) = E |\sin(x)|f(x)=E∣sin(x)∣ ( −π≤x≤π-\pi \leq x \leq \pi−π≤x≤π ) 展开成傅里叶级数，其中 EEE 是正的常数。

解答

所给函数 f(x)f(x)f(x) 在区间 [−π,π][-\pi, \pi][−π,π] 上满足傅里叶级数收敛定理的条件，并且拓展为周期函数时，它在每一点 xxx 处都连续。因此，拓展的周期函数的傅里叶级数在 [−π,π][-\pi, \pi][−π,π] 上收敛于 f(x)f(x)f(x)。

计算傅里叶系数如下：

1. 计算 a0a_0a0​:

由于 ∣sin⁡(x)∣|\sin(x)|∣sin(x)∣ 是偶函数，因此：

1. 计算 ana_nan​:

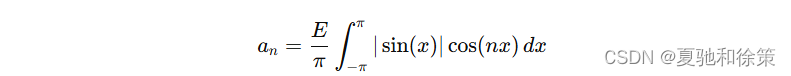
由于 ∣sin⁡(x)∣cos⁡(nx)|\sin(x)| \cos(nx)∣sin(x)∣cos(nx) 是偶函数，因此：

利用三角恒等式：

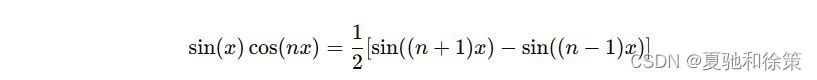
计算积分：

由于 nnn 为整数，上述积分结果为零，因此：

1. 计算 bnb_nbn​:

由于 ∣sin⁡(x)∣sin⁡(nx)|\sin(x)| \sin(nx)∣sin(x)∣sin(nx) 是奇函数，因此：

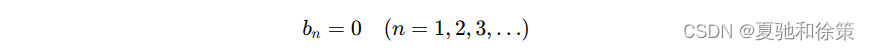
综上，f(x)=E∣sin⁡(x)∣f(x) = E |\sin(x)|f(x)=E∣sin(x)∣ 的傅里叶级数展开式为：

总结

通过上述例题，可以看出傅里叶级数是一种将周期函数展开为三角函数级数的方法。在例题的具体解法中，通过计算傅里叶系数 ana_nan​ 和 bnb_nbn​，再将其代入傅里叶级数展开式，可以得到具体的级数形式。傅里叶级数的图形能够反映出周期函数在不同点的收敛特性，从而为理解复杂波形的组成和分析提供了强有力的工具。

三、正弦级数和余弦级数

概述

一般说来，一个函数的傅里叶级数既含有正弦项，又含有余弦项（见例2）。但是，也有一些函数的傅里叶级数只含有正弦项（见例1）或者只含有常数项和余弦项（见例3）。这是什么原因呢？实际上，这些情况与所给函数 f(x)f(x)f(x) 的奇偶性有密切关系。对于周期为 2π2\pi2π 的函数 f(x)f(x)f(x)，其傅里叶系数计算公式为：

由于奇函数在对称区间上的积分为零，偶函数在对称区间上的积分等于半区间上积分的两倍，因此， 当 f(x)f(x)f(x) 为奇函数时，f(x)cos⁡(nx)f(x) \cos(nx)f(x)cos(nx) 是奇函数，f(x)sin⁡(nx)f(x) \sin(nx)f(x)sin(nx) 是偶函数，故：

即奇函数的傅里叶级数只含有正弦项，称为正弦级数：

当 f(x)f(x)f(x) 为偶函数时，f(x)cos⁡(nx)f(x) \cos(nx)f(x)cos(nx) 是偶函数，f(x)sin⁡(nx)f(x) \sin(nx)f(x)sin(nx) 是奇函数，故：

即偶函数的傅里叶级数只含常数项和余弦项，称为余弦级数：

例 4：线性函数的傅里叶级数展开

题目

设 f(x)f(x)f(x) 是周期为 2π2\pi2π 的周期函数，它在 (−π,π)(-\pi, \pi)(−π,π) 上的表达式为 f(x)=xf(x) = xf(x)=x。将 f(x)f(x)f(x) 展开成傅里叶级数，并作出级数的和函数的图形。

解答

所给函数 f(x)f(x)f(x) 满足傅里叶级数收敛定理的条件，在点 x=(2k+1)πx = (2k+1)\pix=(2k+1)π 处不连续，因此傅里叶级数在这些点处收敛于：

其次，若不计 x=(2k+1)πx = (2k+1)\pix=(2k+1)π，则 f(x)f(x)f(x) 是周期为 2π2\pi2π 的奇函数。显然，此时：

而

将求得的 bnb_nbn​ 代入正弦级数，得 f(x)f(x)f(x) 的傅里叶级数展开式为：

级数的和函数图形

根据上面的计算结果，画出傅里叶级数的和函数图形如下：


数学分析与理解

这个例题告诉我们，通过傅里叶级数可以将一个奇函数 f(x)f(x)f(x) 展开成仅含正弦项的级数，这样可以简化问题的求解过程，并且揭示了函数在不连续点的收敛性。这对于处理复杂的波动问题非常有用。

例 5：绝对值函数的傅里叶级数展开

题目

设 f(x)=∣x∣f(x) = |x|f(x)=∣x∣ 是周期为 2π2\pi2π 的周期函数，它在 (−π,π)(-\pi, \pi)(−π,π) 上的表达式为 f(x)=∣x∣f(x) = |x|f(x)=∣x∣。将 f(x)f(x)f(x) 展开成傅里叶级数。

解答

所给函数 f(x)=∣x∣f(x) = |x|f(x)=∣x∣ 满足傅里叶级数收敛定理的条件，在整个数轴上连续，因此傅里叶级数处处收敛于 f(x)f(x)f(x)。

因为 f(x)f(x)f(x) 是偶函数，所以按公式：

而

由于 ∣x∣cos⁡(nx)|x| \cos(nx)∣x∣cos(nx) 是偶函数，积分可简化为：

傅里叶级数展开式为：

级数的和函数图形

根据上面的计算结果，画出傅里叶级数的和函数图形如下：


数学分析与理解

通过这个例题，我们可以看到，偶函数的傅里叶级数展开只包含常数项和余弦项。通过傅里叶级数展开，我们可以清楚地看到复杂函数可以由简单的余弦函数叠加而成。这种分析在信号处理和热传导问题中有广泛的应用。

例 6：三角函数的正弦级数和余弦级数

题目

将函数 f(x)=xf(x) = xf(x)=x 在 [0,π][0, \pi][0,π] 上分别展开成正弦级数和余弦级数。

解答

正弦级数展开

对函数 f(x)f(x)f(x) 作奇延拓：

计算正弦级数的傅里叶系数 bnb_nbn​：

因此，正弦级数展开式为：

余弦级数展开

对函数 f(x)f(x)f(x) 作偶延拓：

计算余弦级数的傅里叶系数 ana_nan​：

因此，余弦级数展开式为：

数学分析与理解

通过例 6，我们看到，对于定义在 [0,π][0, \pi][0,π] 上的函数，通过奇延拓和偶延拓，可以分别得到其正弦级数和余弦级数展开。这种方法在实际应用中非常重要，特别是在处理周期延拓问题时，可以灵活地选择延拓方式，从而简化问题的分析和求解过程。