
📘 西瓜书笔记 - 5.3 误差逆传播算法(BP算法)
多层神经网络的强大不仅体现在它能拟合更复杂的函数关系,还体现在其训练方法的数学美感与实用价值,而这一切的核心,就是 误差逆传播算法(BackPropagation,简称BP)。
🔍 什么是误差逆传播算法?
相比单层感知机,多层前馈神经网络(如图5.6(b)所示)具有更强的表达能力。但也因此,感知机的简单学习规则(如公式5.1)已无法胜任。BP算法应运而生,其本质是一种基于梯度下降法的链式求导机制,通过计算输出误差的梯度反向传播到各层神经元,进而更新网络参数。
BP算法是当前神经网络最成功、应用最广泛的训练算法之一,也可用于递归神经网络等复杂结构的训练。
📐 算法结构与符号说明
参考图 5.7,假设有如下结构的三层前馈神经网络:
-
输入层维度为 dd
-
隐藏层神经元数量为 qq
-
输出层神经元数量为 ll
连接权重与符号如下:
-
输入层到隐藏层:权重为 vihv_{ih},输入为 xix_i,隐层第 hh 个神经元输入为:

-
隐藏层到输出层:权重为 whjw_{hj},输出层第 jj 个神经元输入为:

其中 bhb_h 为第 hh 个隐层神经元的输出,通常通过 sigmoid 激活函数:

🎯 目标函数:最小化均方误差
对于每个训练样本 (xk,yk)(\boldsymbol{x}_k, \boldsymbol{y}_k),其误差定义为:

🔁 反向传播与梯度推导
输出层梯度项:
由链式法则推导得:

其中:

类似地可得:
隐藏层梯度项:
定义误差传播项:

🔁 算法流程(标准BP算法)
图 5.8 总结了 BP 的训练流程:
输入:训练集 D = { (x_k, y_k) },学习率 η
1. 在 (0,1) 范围内初始化权值与阈值
2. repeat
3. for 每个训练样本 (x_k, y_k):
4. 前向传播,计算输出 \hat{y}_k
5. 计算输出层误差项 g_j
6. 反向传播误差到隐层,得到 e_h
7. 更新权值 w_{hj}, v_{ih} 和阈值 θ_j, γ_h
8. until 停止条件满足
目标是最小化整体累积误差:

🎯 累积BP vs 标准BP
-
标准BP算法:每轮迭代针对一个样本更新参数(类似 SGD)
-
累积BP算法:每轮遍历所有样本后再统一更新(类似 Batch GD)
图 5.9 展示了在西瓜数据集上随着训练轮数的增加,参数与分类边界如何演化。
⚠️ 过拟合与缓解策略
BP神经网络容易过拟合。常用的缓解策略:
-
早停法(Early Stopping): 使用验证集监控误差,验证误差上升时提前终止训练。
-
正则化(Regularization): 在目标函数中加入连接权与阈值的平方项,例如:

🌎 局部极小与全局最小
BP算法只保证局部收敛。由于激活函数非线性,误差函数非凸,局部极小点广泛存在:
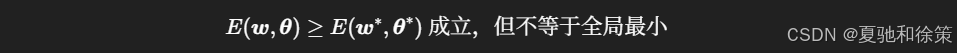
因此,初始化、学习率调整与正则化设计对性能有着重大影响。
✨ 小结
-
BP是深度学习中的基石算法。
-
其核心思想是通过梯度下降,将输出误差“反传”到每一层神经元。
-
标准BP更快,累积BP更稳。
-
常搭配早停、正则化、合适初始化等技术缓解过拟合与局部最小。
📘 下一节我们将学习 5.4 节《全局最小与局部极小》,继续深挖优化目标函数的数学细节与网络学习能力的极限。


























 1188
1188

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










