python实现神经网络

声明：本文是A Neural Network in 11 lines of Python学习总结而来，关于更详细的神经网络的介绍可以参考从感知机到人工神经网络。

如果你读懂了下面的文章，你会对神经网络有更深刻的认识，有任何问题，请多多请教

Very simple Neural Network

首先确定我们要实现的任务：

$\qquad\qquad\qquad\qquad$

输出的为样本为$X$为4*3，有4个样本3个属性，每一个样本对于这一个真实值y,为4*1的向量，我们要根据input的值输出与y值损失最小的输出。

Two Layer Neural Network:

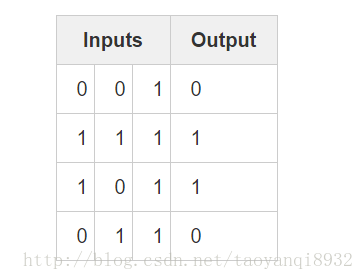
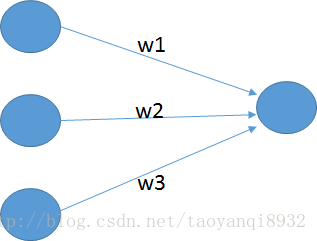
首先考虑最简单的神经网络，如下图所示：

$\qquad\qquad\qquad\qquad\qquad$

输入层有3个神经元(因为有3个属性),输出为一个值，w1,w2,w3为其权重。输出为:

$$f(w1*x1+w2*x2+w3*x3)$$
这里的f为sigmoid函数：
$$f(x)=\frac{1}{1+e^{-x}}$$
一个重要的公式：
$$\frac{df(x)}{dx}=f(x)(1-f(x))$$

神经网络的优化过程是：

1. 前向传播求损失
2. 反向传播更新w

简单是实现过程如下所示：

import numpy as np

# sigmoid function
# deriv=ture 是求的是导数
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))

# input dataset
X = np.array([  [0,0,1],
                [1,1,1],
                [1,0,1],
                [0,1,1] ])

# output dataset            
y = np.array([[0,1,1,0]]).T

# seed random numbers to make calculation
np.random.seed(1)

# initialize weights randomly with mean 0
syn0 = 2*np.random.random((3,1)) - 1

# 迭代次数
for iter in xrange(10000):

    # forward propagation
    # l0也就是输入层
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))

    # how much did we miss?
    l1_error = y - l1

    # multiply how much we missed by the 
    # slope of the sigmoid at the values in l1
    l1_delta = l1_error * nonlin(l1,True)

    # update weights
    syn0 += np.dot(l0.T,l1_delta)

print "Output After Training:"
print l1

注意这里整体计算了损失，X(4*3) dot w(3*1) = 4*1为输出的4个值，所以
l1_error = y - l1同样为一个4*1的向量。

重点理解：

    # slope of the sigmoid at the values in l1
    #nonlin(l1,True),这里是对sigmoid求导
    #前向计算，反向求导
    l1_delta = l1_error * nonlin(l1,True)

    # update weights
    syn0 += np.dot(l0.T,l1_delta)

下面看一个单独的训练样本的情况，真实值y==1,训练出来的为0.99已经非常的接近于正确的值了，因此这时应非常小的改动syn0的值，因此：

$$weight\_update = input\_value * l1\_delta$$

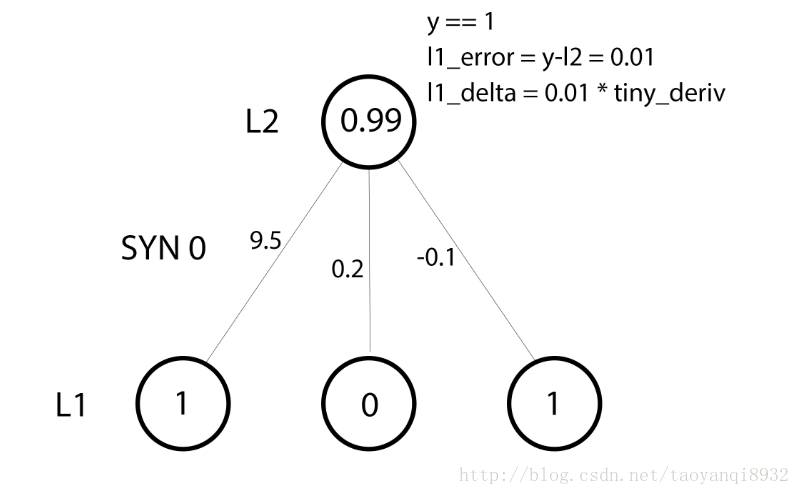
运行输出结果为，可以看到其训练的不错：

Output After Training:
Output After Training:
[[ 0.00966449]
 [ 0.99211957]
 [ 0.99358898]
 [ 0.00786506]]

Three Layer Neural Network:

我们知道，两层的神经网络即为一个小的感知机（参考：感知机到人工神经网络），它只能出来线性可分的数据，如果线性不可分，则其出来的效果较差，如下图所示的数据：

$\qquad\qquad\qquad\qquad$
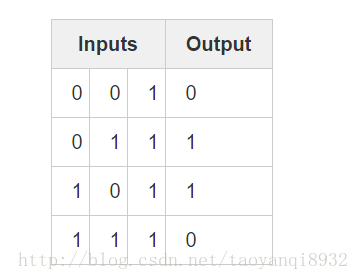
如果仍用上述的代码(2层的神经网络)则其结果为：

Output After Training:
[[ 0.5]
 [ 0.5]
 [ 0.5]
 [ 0.5]]

因为数据并不是线性可分的，因此它是一个非线性的问题，神经网络的强大之处就是其可以搭建更多的层来对非线性的问题进行处理。

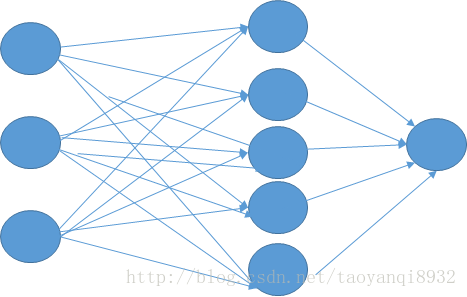
下面我将搭建一个含有5个神经元的隐含层，其图形如下，（自己画的，略丑），这来要说下神经网络其实很简单，只要你把层次的结果想清楚。

要搞清楚w的维度：第一层到第二层的w为3*5，第二层到第三层的W为5*1，因此还是同样的两个步骤，前向计算误差，然后反向求导更新w。
完整的代码如下：

import numpy as np

def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)

    return 1/(1+np.exp(-x))

X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])

y = np.array([[0],
            [1],
            [1],
            [0]])

np.random.seed(1)

# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,5)) - 1
syn1 = 2*np.random.random((5,1)) - 1

for j in xrange(60000):

    # Feed forward through layers 0, 1, and 2
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))
    l2 = nonlin(np.dot(l1,syn1))

    # how much did we miss the target value?
    l2_error = y - l2

    if (j% 10000) == 0:
        print "Error:" + str(np.mean(np.abs(l2_error)))

    # in what direction is the target value?
    # were we really sure? if so, don't change too much.
    l2_delta = l2_error*nonlin(l2,deriv=True)

    # how much did each l1 value contribute to the l2 error (according to the weights)?
    l1_error = l2_delta.dot(syn1.T)

    # in what direction is the target l1?
    # were we really sure? if so, don't change too much.
    l1_delta = l1_error * nonlin(l1,deriv=True)

    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)
print l2

运行的结果为：

Error:0.500628229093
Error:0.00899024507125
Error:0.0060486255435
Error:0.00482794013965
Error:0.00412270116481
Error:0.00365084766242
# 这一部分是最后的输出结果
[[ 0.00225305]
 [ 0.99723356]
 [ 0.99635205]
 [ 0.00456238]]

如果上面的代码看懂了，那么你就可以自己搭建自己的神经网络了，无论他是多少层，或者每个层有多少个神经元，都能很轻松的完成。当然上面搭建的神经网络只是一个很简单的网络，同样还有许多的细节需要学习，比如说反向传回来的误差我们可以用随机梯度下降的方法去更新W,同时还可以加上偏置项b，还有学习率 $\alpha$ 等问题。