我理解的SVPWM(一)

最新推荐文章于 2025-03-21 20:08:12 发布

HappytoShareMotor

最新推荐文章于 2025-03-21 20:08:12 发布

阅读量3.9k

点赞数 10

分类专栏：电机与电机控制文章标签： c语言 mcu 单片机驱动开发

原文链接：https://zhuanlan.zhihu.com/p/412168396

版权

电机与电机控制专栏收录该内容

8 篇文章

订阅专栏

文章转载自(知乎及微信账号HappytoShare)

我理解的SVPWM(一)https://zhuanlan.zhihu.com/p/412168396https://zhuanlan.zhihu.com/p/412168396 我理解的SVPWM(一)https://mp.weixin.qq.com/s?__biz=MzI2MjExNDMzNQ==&mid=2247484318&idx=1&sn=d27dcc27784a8789600a81fed54ae1f8&chksm=ea515eeedd26d7f86c3b0d97e6ee80f7922050e7fdaf7e1b94136bdf22a361c08c83369f0427&token=1328820438&lang=zh_CN#rdhttps://mp.weixin.qq.com/s?__biz=MzI2MjExNDMzNQ==&mid=2247484318&idx=1&sn=d27dcc27784a8789600a81fed54ae1f8&chksm=ea515eeedd26d7f86c3b0d97e6ee80f7922050e7fdaf7e1b94136bdf22a361c08c83369f0427&token=1328820438&lang=zh_CN#rd

本文

将介绍到：

基本电压矢量及电压矢量圆
为什么最大矢量圆半径是 $\sqrt{3}/2*V_{dc}$
为什么空间矢量的边界是六边形
各扇区内基本矢量作用时间计算

一、一般约定

在本文中，我们先做如下约定：

1. 线电压指电机三相绕组中任意两相绕组端点之间的电压，如 U_{UV} ；

2. 相电压指电机三相绕组中任意一相端点到电机绕组中心点O的电压，如 U_{UO} ；

3. 端电压指电机三相绕组中任意一相端点相对于GND的电压，如 U_{UG} ；

4. 中性点电压指电机三相绕组的中性点相对于GND的电压，如 U_{OG} ；

二、基本电压矢量及电压矢量圆

大多数人最初接触电机控制时了解的可能是两两导通三相六状态的方波控制方式。这种控制方式根据电机的位置来选择导通不同桥臂上下各一个MOS管，理解起来比较容易。SVPWM与这种控制方式不同，SVPWM调制方式是将UVW三个桥臂分别定义为0,1两种状态，规定：

0代表下管开通上管关断；
1代表上管开通下管关断；

至于为什么这样，可能要去翻一番SVPWM的发展历史了，我们就姑且认为有人发现了这么一种控制方式，将桥臂按照如上所述定义。

三个桥臂的两种状态总共有八个组合，产生的结果如下：

这里为了便于记忆，我们将3位二进制与十进制的0-7对应起来。如下图，第一个桥臂是W相，它的数值为0，说明它的下MOS是导通的。第二个桥臂是V相，它的数值为1，说明它的上MOS是导通的。第三个桥臂是U相，它的数值是0，说明它的下MOS是导通的。这里与大家平时习惯的UVW(有些文献喜欢用ABC)顺序相反，但是后面所有的推导都是以U轴中心线和X轴正方向一致，V轴中心线在逆时针120度位置，W轴中心线在逆时针240度位置，所以结果是普遍适用的。采用此方法是方便记忆六扇区的矢量合成图分布。

图2

八个导通状态如下：

000 - v0 (zero vector)
001 - v1 (Phase +U)
010 - v2(Phase +V)
011 - v3 (Phase -W)
100 - v4(Phase +W)
101 - v5 (Phase -V)
110 - v6(Phase -U)
111 - v7 (zero vector)

下面通过电机控制的简图说明以上8种状态。这里用双向导通开关替代了上桥臂MOS和下桥臂MOS。当开关连接到上端，则上MOS导通。当开关连接到下端，则下MOS导通。

图3 000 - v0 (zero vector)

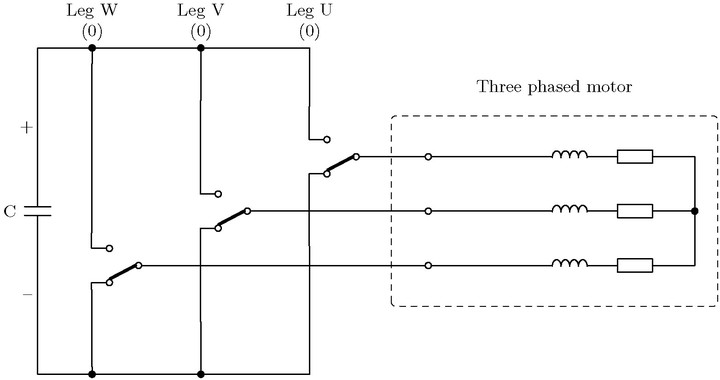
图4 001 - v1 (Phase +U)

图5 010 - v2(Phase +V)

图6 011 - v3 (Phase -W)

图7 100 - v4(Phase +W)

图8 101 - v5 (Phase -V)

图9 110 - v6(Phase -U)

图10 111 - v7 (zero vector)

熟悉了以上八种导通状态后，接下来分析各通电状态下，各相电压的大小以及合成电压矢量大小及方向。

如下图，U相桥臂的上管开通，下管关闭。V相和W相桥臂的上管关闭，下管导通。现规定电流从各相端口流入中性点为电流正方向，从中性点流出端口为负方向。则U相的电流为正，V/W相的电流为负。假设电机各相的阻抗相等，都为Z，则根据基尔霍夫电流定律，流过U相的电流是流过V/W相电流的2倍。计算各端口相对电机中性点的电压可以得到各相相电压如图所示，这里计算的中性点电压是相对于GND的，其他相电压都是端电压相对中性点的压降。根据右手定则，可得各相的磁场方向。同理，可以推广到电压矢量，如图右下角所示，可以计算得到三相电压合成矢量的数值为Udc，方向如图所示。为了便于理解相电压的计算，在本图中将右侧的星形电机内部绕组模型也与左边的MOS电路进行了连接。其实，左边已经有了电机绕组，这里大家清楚是为了表达而加的连接线即可。

图 11 001 - v1 (Phase +U)

关于其他导通状态与上图类似，这里直接给出结果，省略了文字描述。

图12 010 - v2(Phase +V)

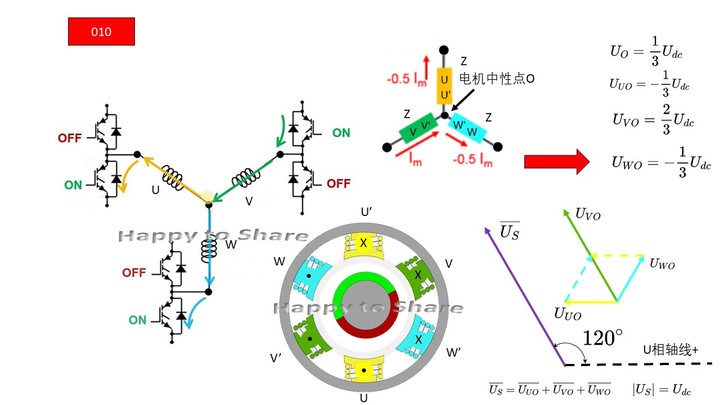
图13 011 - v3 (Phase -W)

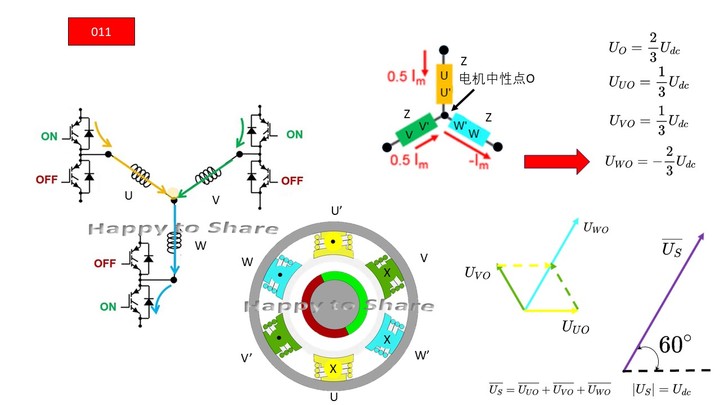
图14 100 - v4(Phase +W)

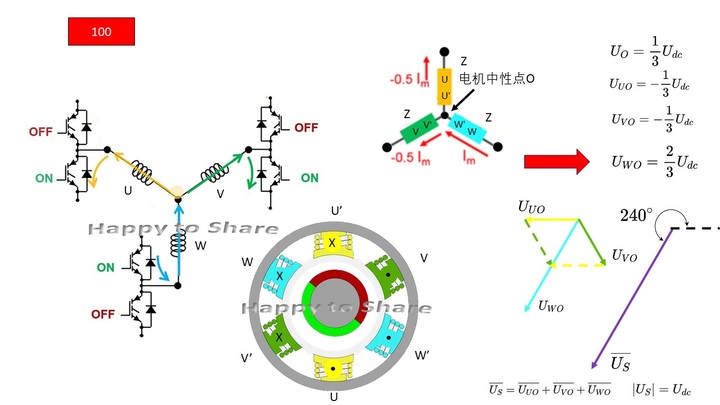
图15 101 - v5 (Phase -V)

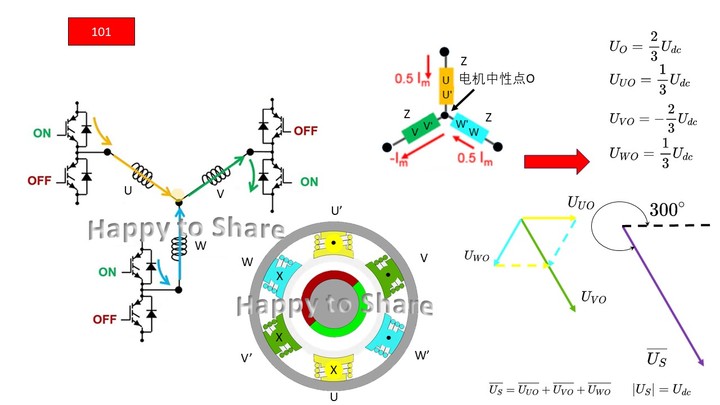
图16 110 - v6(Phase -U)

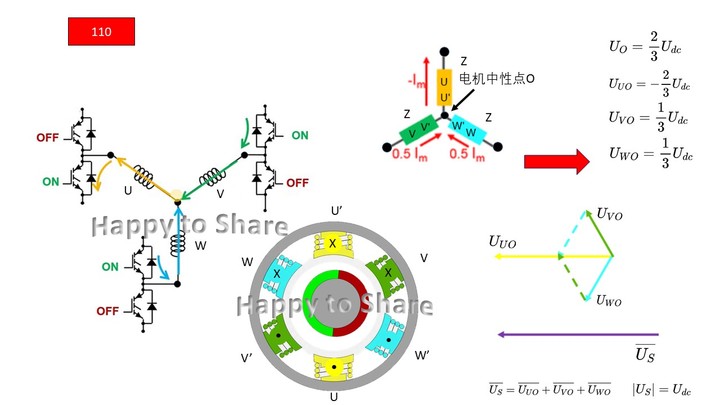
以上六张图包含着大量的信息，我们来梳理一下。

线电压和相电压

这里提到的相电压是各端点相对于Y绕组中心的电压，线电压是两个端点之间的电压。可总结如下图：

图17

2. 8种通电状态下的基本矢量位置

如下图，6个导通状态下的电压矢量，加上000和111两个0矢量。为了快速记忆这张图各矢量的位置，可以将V1矢量与电机三相坐标系的U轴轴线正方向一致，则在120度位置的V轴与V2(010)重合，正好只有中间代表V桥臂的2进制为1(参见图2)。同理，在240度位置的W轴与V4（100）重合，因为100只有代表W相的2进制为1(参见图2)。两个相邻基本相量的间隔是60度，则剩余的空间矢量(相量)很好确定位置。比如，60度位置的相量就是V1和V2两个二进制的和，即：001 + 010 = 011 = V3。同理，可以在不参考任何资料的情况下快速将各基本矢量画出来。基本矢量的长度为Udc，上面图11-16中均有计算。

图18：

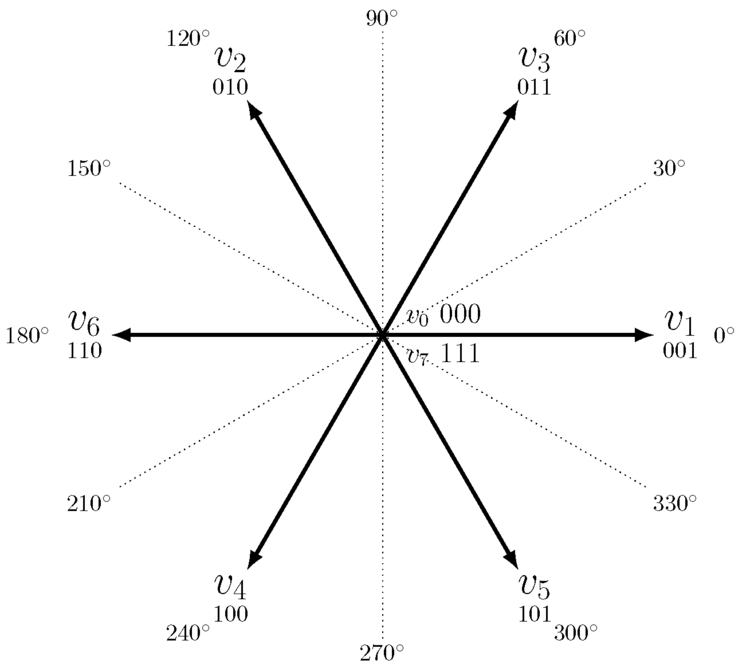
但是，如果按照这么来控制电机就类似于方波BLDC电机的6步换相控制了，每60电角度度切换一次导通状态，容易引起扭矩波动。尽量减少两个矢量切换之间的角度可以降低扭矩波动。为此，我们把60电角度的区域称之为一个扇区，如下图所示。

图19

如下图，在每个扇区内部，我们让矢量尽量均匀旋转，这样电机的扭矩波动就会降低。那好，怎么来实现60度内的矢量分布？

图20

如下图，任取第一扇区内的任一矢量，根据平行四边形原则，可以将其分解为沿V1和V2的量。也就是说我们可以根据相邻的两个基本矢量和一个或两个矢量(000或者111)计算它们所围成的扇区内的任意矢量的幅值和方向。这里，T代表的是采样周期，一般是PWM的周期，V1的作用时间是T1，V2的作用时间是T2，则0矢量的作用时间为T-T1-T2。

图21

到此，我们也就引出了SVPWM控制的基本思想。

三、最大矢量圆半径 $\frac{\sqrt{3}}{2}V_{dc}$

通过第二节我们建立了UVW三相坐标下的空间矢量图(注意这里不是 $\alpha\beta$ 坐标系)，其基本矢量的模长为Udc。接下来，我们再来思考一个问题，在每个扇区内，由两个基本矢量和零矢量合成的最大矢量圆半径是多少？为了推导这个问题，我们拿第一扇区为例进行说明。如下图，单独取出第一扇区并将其放大，第一扇区的两个基本矢量是V1和V3，零矢量可以为V000或者V111。

图22

在第一扇区内任意的矢量 $V_{ref}$ ，应该是这三个矢量的合成。即：

$V_{\text {ref }}=\vec{V} 1 \frac{T 1}{T}+\overrightarrow{V 3} \frac{T 2}{T}+V_{000} \frac{T-T 1-T 2}{T}$ (1)

结合图21，将 $V_{ref}$ 在V3和垂直于V3方向投影，可得

$T 1=\frac{2 T V_{r e f}}{\sqrt{3} V_{d c}} \sin \left(\frac{\pi}{3}-\theta\right)$ （2）

结合图22，将 $V_{ref}$ 在V1和垂直于V1方向投影，可得

$T 2=\frac{2 T V_{r e f}}{\sqrt{3} V_{d c}} \sin \theta$ （3）

零矢量的作用时间：

T0 = T - T1-T2 (4)

零矢量的模长为0，对合成矢量的模长没有作用。所以合成矢量的最大幅值应该出现在零矢量的作用时间为0时，也就是T= T1 + T2。T1为基本矢量V1的作用时间，T2为基本矢量V3的作用时间，T代表PWM周期。

正常情况下，T1+T2小于等于T(当T0=0时取等号)，因为物理世界不可能插入负的T0。因此，正常工况下:

$T1+T2\leq T$ (5)

根据T1和T2的计算公式可得：

$T 1+T 2=\frac{2 T V_{r e f}}{\sqrt{3} V_{d c}} \sin \left(\frac{\pi}{3}+\theta\right)$ (6)

由式（5），可得

$\frac{T 1+T 2}{T} \leq 1$

于是，

$\frac{T 1+T 2}{T}=\frac{2 V_{\text {ref }}}{\sqrt{3} V_{d c}} \sin \left(\frac{\pi}{3}+\theta\right) \leq 1$ （7）

其中， $0 \leq \theta \leq 60^{\circ}$ 。

则， $60^{\circ} \leq \theta+\frac{\pi}{3} \leq 120^{\circ}, \frac{\sqrt{3}}{2} \leq \sin \left(\theta+\frac{\pi}{3}\right) \leq 1$

令，

$K=\frac{2 V_{r e f}}{\sqrt{3} V_{d c}}$

K一定是一个小于等于1的数！

否则当 $\theta+\frac{\pi}{3}=\frac{\pi}{2}$ 时， $\frac{T 1+T 2}{T}$ 就会大于1，这也就是说需要插入负的T0，这在物理世界是无法实现的。

所以，

$K=\frac{2 V_{r e f}}{\sqrt{3} V_{d c}}\leq 1$

可得，

$V_{r e f} \leq \frac{\sqrt{3}}{2} V_{d c}$ （8）

取最大值， $V_{r e f}=\frac{\sqrt{3}}{2} V_{d c}$

得，

$\frac{T 1+T 2}{T}=\frac{2 V_{r e f}}{\sqrt{3} V_{d c}} \sin \left(\frac{\pi}{3}+\theta\right)=1$

将， $V_{r e f}=\frac{\sqrt{3}}{2} V_{d c}$ ，带入得 $\theta = 30^{\circ}$ 。

将， $\theta = 30^{\circ}$ 带入式（3）

可得，

$\frac{T2}{T} = \frac{1}{2}$

可知，在30电角度时若要取得最大的电压合成矢量，则T1 = T2 = T/2(T0矢量作用时间为0)。

根据以上信息，可以画出最大矢量圆，如下图绿色圆，所有的电压矢量要落在该矢量圆内部，以便进行线性调制。超出该圆后就成为过调制，有对应的处理办法。

图23

当超出该最大矢量圆半径后，在某些角度下，计算得到的T0作用时间为负值，如下图所示。

图24

四、为什么空间矢量的边界是六边形

有关空间矢量分析的论文和网络文章很多，但是极少有深入介绍为什么空间矢量的边界是六边形。大部分都是在推导出基本矢量后就直接默认给出这个六边形，并直接给出结论说合成矢量不能超越这个六边形边界，没有给出理论公式，也没有直观叙述。

在看文献时，这个问题困惑了我很久。现在就将自己的一点直观理解放在这里，作为抛砖引玉，希望有大神可以出来给大家更好的解释。

SVPWM是用伏秒平衡的原理来用基本矢量等效平均合成矢量。六边形出现在每60度电角度内不进行PWM调制(six-step mode)或者说出现在当整个扇区内T0都等于0的情况。

当不进行PWM调制时，每隔60度电角度合成矢量变换一次，类似于方波控制的六步换相。以第一扇区为例，本来合成矢量的大小是V1,并且持续大约60度电角度，不进行任何MOS开关的切换。当转过大约60度电角度时需要切换为合成矢量V2，这时存在一个切换过程，这个过程中V1逐渐减小，V2逐渐增加。它们的合成矢量便沿着六边形在第一扇区的边进行过渡。整个过程始终没有T0的参与。

图25