无理数存在性的几何证明

大家知道毕达哥拉斯的名字，是由于那个尽人皆知的定理，这个定理在中国被叫做勾股定理，但很多人不知道以他命名的学派，更不知道这个学派中曾经发生的一个重要事件，这个事件就是无理数的发现。无理数的发现引发了数学上的异常重要风波，它被称为第一次数学危机，而它的发现者也因为破坏了学派创始人的信仰，被残酷的抛入大海。本文用图形化的方式，通过一个例子，来说明无理数存在的合理性。由于受到当时哲学的影响，毕达哥拉斯学派认为世界的物质是由"原子”构成的，但是这里的原子并不是我们现代意义上的原子。基于这一看法，它们提出了一条公设.,这个公设断言：

任意两条直线段均有公度

更具体的说，若与为任意两条直线段的长度，则存在一条直线，其长度为,使得

所以:

通过公倍操作，总可以有办法，使m,n是正整数，如下图所示：

如果把

看作单位长度,它就是我们要找到公度长度，n个单位长度就是b,而m个单位长度就是a.

这个过程怎么看怎么像用辗转相除法取最大公约数的过程。注意，这里的整数条件很重要，后面几何证明的时候，要用到这个条件推出矛盾。

也就是说，毕达哥拉斯学派认为：对于任何两个直线段长度，都存在一个长度，在两个线段上都可以放置整数次，所以线段之比可以用整数之比来表示，这种朴素的认知来源于经验，爱因斯坦说过: 数学作为独立与经验的人类思维的产物，为何与物理现实中的客体如此吻合?没有经验依据，而只靠纯粹思维，人类就能够发现实际事务的性质吗？只要数学的命题是涉及实在的，他就是不可靠的;只要它是可靠的，他就不涉及实在．或则和简单论述为，数学法则只要与现实有关，都是不确定的，若是确定的，都于现实无关。量的精确化超过一定限度，总要产生质的变化，比如，气压如果精确到超过一个分子的撞击力大小时，是没有意义的，当电量描述超过个一个电子所带电荷的程度时，是没有意义的，如果原子直径是最小的度量，那所有物体的尺寸都是可公度的。对于数学中的理论证明，要通过纯粹的逻辑推导和形式化的思辨才能达到.

无理数发现者对这个结论说不，他们认为，存在不可通约的量，在这种情况下，你找不到一个公度长度量，使两个长度都是公度量的整数倍。

无理数存在的例子

看下面的等腰直角三角形,当然我们现在知道,因为是无理数，所以是不可通约量，不能由有理数分式表示，但是现在，我们假设不知道这个前提，也不知道勾股定理，看能推导出什么。

分别表示角对应对边的长度，证明不可通约，也就是证明不可通约，用反证法，假设存在一个通约量，使

则

如果存在通约量d,不管它是整数还是小数，我们总能找到m,n是正整数，这是一个很重要的条件，后面将用它推导出矛盾。

我们绘制辅助线，以A为圆心，AC为半径做圆，交AB于D点，然后再过D点做AB的垂线，交BC于E.容易证明：

代入上等式成立。

也就是说，如果d是等腰直角三角形的斜边和直角边的通约量，那么它同样也是等腰直角三角形的斜边和直角边的通约量。

同样的辅助线我们可以继续往下画，继续往下推导，由于m,n是正整数，而计算出来的下级等腰直角三角形的边长始终是d的整数被的和差，基于这个原因，会得到一个结论，那就是，如果一直画下去，任意子级的等腰直角三角形的斜边和直角边都有同一个可通约量d.d是所有这些等腰直角三角形的公度。

这个结论肯定是错误的，m,n是有限的正整数，这一过程不可能无限做下去，三角形越来越小，必然会出现三个边都小于d的情况，怎么可能公度一直都是d呢。这样就产生了矛盾。

而这个结论是我们承认“存在可通约量d"的必然结论，所以，只能说明我们的前提一开始就错了，也就是说，根据排中律，不存在这样的d，使得

所以，通过绘制等腰直角三角形，我们得到了两条无法通约的线段，正方形的边和对角线不可公度。

---

证明的过程很自然，也找不到破绽，但是总觉得还是缺一点东西，比如，为了证明命题不可通约成立，用了反证法，用几何方式构造出矛盾，从而证明了原命题。但是直角三角形有很多种，比如通常用来说明勾股定理成立的直角边3，4，斜边5的直角三角形，它的斜边与直角边之比分别为，就是可以通约的，至少存在通约量1。那问题就来了，同样的证明过程是否能够使用3,4,5边长构成的三角形上，如果同样的证明过程适用于后者，那就是说同一个证明逻辑既可以证明通约，又可以证明不可通约，那证明逻辑就有问题。

当然，这个证明没有问题，有问题的是我们对后者的逻辑，现在就看看对于3,4,5的三角形，上面的证明逻辑那里不适用，在斜边和直角边可通约的情况下，上述的证明一定会有某种变化，否则就会出现和事实（3,4,5可通约）相背离的矛盾。

同样，对于边长比例为3,4,5的三角形，假设通约量d. 

同样的方式，我们绘制辅助线和辅助圆，得到以下结论：

根据相似性：

所以，

所以，看出来了吗？虽然我们仍然可以像等腰直角三角形那样一直进行下去，可是从第二个直角三角形开始，d的系数已经是不是整数，就是这个根本差异，导致了同样的过程推到不出同样的结论，等腰直角三角形的情况下，在假设成立必然推出腰线始终被控制在d的整数倍，所以矛盾不可避免。

但是对于第二种可以通约的情况，则没有这种限制，边长系数出现了小数，说明我们可以通过对d再抽取一层和系数相乘划归为整数继续进行下去，斜边和直角边仍然是可规约的，只不过这时候通约量变成了,而不是原来的d了，这样就绕开了矛盾，可以一直画下去而保持通约,永远无法找到和题设之间的矛盾，因为本来3，4，5三个边都是可通约的么，推导不出矛盾来。

所以，我们消除了疑虑，通过几何图形化方式证明无理数的存在是可行的。

无理数与有理数有一个重大差别：无理数不可能有一个由整数和四则运算组成的表达式表达。有理数有一个有限的表达式，就是整数分式，但无理数没有。无理数与无穷有千丝万缕的联系，当用小数表示时，它是无限不循环的，需要无穷多个位数，包含无穷多的信息，用连分数表示式，是一个无穷的连分式，用级数表示，是无穷多项级数的累加。它与有理数有着本质的不同。

就拿圆周率来说，在超级计算机的帮助下，现在已经计算出了的前一百万亿位，即便如此，我们甚至都不能说“差不多”计算出了，因为还有“无穷多”的位我们还不知道。

看另一个更漂亮的几何证明：

如果存在最小的整数p,q（约化之后的).

则

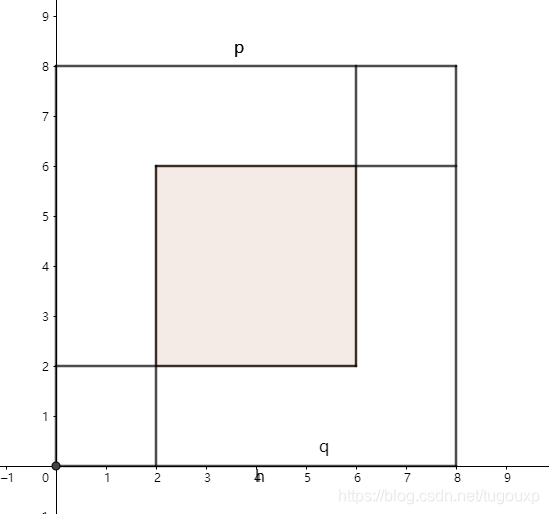
我们用一个边长为p的大正方形内部套着两个边长为q的小正方形为例来说明，注意内部的两个正方形一定有重叠（假如没有重叠，肯定不成立），重叠的深色部分也是一个正方形。

则根据初等几何知识，如果，我们可以得出：

中间深色部分正方形的面积=左下角小正方形面积+右上角小正方形面积=2*两个小正方形任意一个面积

假如中间正方形边长是s,小正方形面积是m.

则

成立。并且s=2q-p, m=p-q都是整数。

等等，刚刚不是说了，p,q是最小的满足的整数吗？s,m哪里来的？ 矛盾！

完善证明

证明过程中，依据“这一过程不可能无限做下去，三角形越来越小，必然会出现三个边都小于d的情况”推导出了矛盾，但是这个计算为什么不可能无限做下去呢？

可以利用自然数的良序原理(well-ordering principle)说明不可能无限做下去，最小数原理是自然数所具有的一种基本性质，即任何非空的自然数集中都有最小的自然数，该原理可以推广到整数集，有理数集。完整表达是：

良序原理指出，自然数集的每个非空子集都有个最小元素，即自然数在其标准的大小关系下构成一良序集。

数学证明存在性问题的两种方式

要证明一个数学命题：存在一个x满足A。如果能具体地给出满足性质A的一个或能找到一个机械的程序，使按其进行有限步骤后，就能确定满足性质A的这个x。这样的方法称为构造性方法。与之相比较，数学中应用反证法作的纯存在性的证明称为非构造性方法。

打个比方：构造法的成功使用，解题人就像一个精明的“建筑师”，不仅要思考作为已知信息的“建筑材料”，还要时刻记住将要搭建的“建筑”，即符合命题要求的事物。构造方法就是对应的建筑方法啦！

运用构造法，可以使代数、三角、几何等各种数学知识互相渗透，有利于问题的解决。其目的是通过构造的图形等提示已知与未知的关系，确定论证的出发点，使证题思路豁然开朗。

总结：

也许无理数是人类追求数学的美所付出的代价，人类创造了这个虚拟世界（只有在这里，度量才是真正可能的），现在必须去面对它所带来的问题，不能够用分数表示的数，就是无理数，英文叫做irrational，不成比例的意思，它们很自然的出现在几何学中，我们必须学会去适应它，正方形的对角线恰好是其边长的根号2倍，这就是我们所知道的关于它的全部，我们只知道这个数的平方是2，我们并不能说出这个值到底是多少，虽然可以粗略的估计它，但是除此之外，我们一无所知。

补充：

无理数的命令有一个小小的误会，无理数最早是希腊人发现的，他的最初意思并不包含“理性”或者“无理”的意思，而是纯粹说明一种“不可表达的”数，只是后面在翻译成拉丁文过程中出现了偏差，后面的翻译将错就错，造成了一个数学上的一个误解。

无理数的发现使毕达哥拉斯的万物皆数的理论就出现了一个漏洞，存在线段的长度无法用整数比进行度量，据说西帕索斯因为这个发现而遭到杀害，毕达哥拉斯学派担心这个秘密被泄漏出去，而把西帕索斯投入大海。

历史的车轮不会倒退，古希腊的哲学家和数学家们正视了这个问题，经过欧几里德等人的工作，最终严格定义了不可公度和无理量，纳入了数学体系。

几何原本中对不可公度的定义：

如果从两个不等量的大量中连续减去小量，直到余量小于小量，在从小量中连续减去余量直到小于余量，这样一直做下去，当所余的量总不能量尽它前面的量时，则称两个量不可公度。

这里出现了一个有意思的现象，不可公度是用欧几里德算法能够停下来定义的，由于欧几里德算法是递归的，也就是说递归能否终止成了判断条件。递归和物理量似乎存在着某种深刻的联系，或许蕴含着递归的本质，分形的本质。

无理数都没有规律么？

无理数是无限不循环小数，在我们的印象中，无限不循环小数就意味着混乱，没有规则，这个印象主要来源于我们常见的一些无理数，比如π，e, √2等，看起来都是乱糟糟的，没有规律，而且无穷无尽。但是违反直觉的是，并不是所有的无限不循环小数都是乱糟糟的，比如这个数字：

0.10100100010000.....等等，它也是无限步循环的，但是却很有规律，我们甚至可以写出它的通项公式出来：

所以无限步循环并不达标没有规律，它这是没有循环这一种规律而已，但是可以有其他的规律。我们可以模仿周期函数来区分无限循环小数和无限不循环小数。

---

结束！