LoRA构建：利用数学知识进行低阶自适应分析并在 PyTorch 中实现

公众号：Halo 咯咯

本文中将介绍了解 LoRA 是什么，并用数学原理知识来描述 LoRA 有效微调大型模型，最后从头开始创建我们自己的 LoRA 并使用它来微调我们的模型。

LoRA是如何工作的？

LLM（Large Language Models，大型语言模型）和其他类似的先进模型，例如稳定扩散模型，通常拥有数十亿个参数，这使得它们在处理复杂的人工智能任务时表现出色。然而，这种规模的模型需要庞大的预算和计算资源才能进行有效的微调，以适应特定的业务场景。
为了解决这一挑战，微软在其研究论文《LoRA: Low Rank Adaptation of LLMs》中提出了一种创新的方法——LoRA。LoRA的核心思想是优化微调过程，减少对计算资源的需求。
在传统的微调过程中，通常需要将整个模型加载至GPU，并执行反向传播算法来更新模型的所有权重。但LoRA采取了一种不同的路径。它通过冻结原始模型的初始权重W，并引入两个额外的低秩矩阵A和B来实现微调。这两个矩阵的乘积将生成一个新的权重矩阵，其维度与原始权重矩阵W相同。
在训练过程中，只有LoRA矩阵参与反向传播，而原始模型的权重保持不变。这样，LoRA大幅减少了在微调过程中需要更新的参数数量，从而降低了对计算资源的需求。这种方法不仅提高了效率，还使得在有限的资源下对大型模型进行微调成为可能，为各类企业打开了利用先进AI技术的大门。

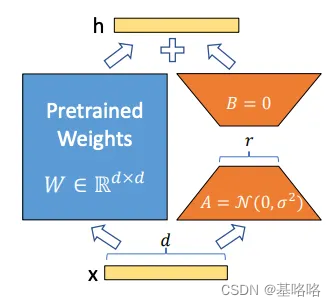
正如之前提到的，LoRA（Low Rank Adaptation）的核心技术机制是基于矩阵分解的。这种方法允许我们在训练过程中以一种高效的方式来调整和优化模型的权重。

LoRA的数学原理

在LoRA的前向传递过程中，我们使用以下公式来计算隐藏层h：

h = W0 + ΔW

其中，h代表的是模型的隐藏层表示，W0是预训练模型中冻结的原始权重矩阵，其形状为(d x k)，这里的d表示特征的维度，k表示模型的容量或者隐藏单元的数量。ΔW则是LoRA技术所特