漫步线性代数七——特殊矩阵和应用

本篇文章有两个目标。第一是解释实际问题中大型线性方程组$Ax=b$的一种解法，事实是，工程或经济学中大型和现实的问题能够引导我们更深入理解这些知识。但是有一个很重要应用却不需要大量的准备工作。

另一个目标是说明系数矩阵具有的一些特殊性质，为了方便我们用同一个应用进行讲解。大型矩阵几乎总是有一个清晰的模式-对称和很多零元素。因为一个稀疏矩阵包含的信息远小于$n^2$个，所以计算应该更快。我们将观察带状矩阵，看看集中在对角线附近是如何加快消元的，为此我们将看到一个特殊的三对角矩阵。

看方程(6)中的矩阵，它是通过将微分方程变化为矩阵方程得到的。这是对每个$x$求$u(x)$的连续问题，很明显计算机不能解决它，所以它必须近似为一个离散的问题-我们保留更多的未知变量，结果的精度就越好，当然计算代价也就越高。作为一个简单但仍然具有代表性的连续问题，我们选择微分方程

$$\begin{equation} -\frac{d^2u}{dx^2}=f(x)\qquad 0\leq x\leq 1\tag1 \end{equation}$$

这是关于位置函数$u(x)$的线性方程，可以在解中加上任何组合$C+Dx$依然满足要求，因为$C+Dx$的二阶导为零，不影响结果。对于两个任意常数$C,D$的不确定性，通过在区间的两端添加一个边界条件就能够移除：

$$\begin{equation} u(0)=0,\quad u(1)=0\tag2 \end{equation}$$ 这个结果是一个两点边值问题，描述的不是瞬变而是稳态现象-例如一根棒的温度分布，它的一端固定为 $0^0C$并且热源为 $f(x)$。

记住，我们的目标是产生一个离散的问题-换句话说，一个线性代数中的问题。为此我们只可以接受$f(x)$有限的信息，描述在$n$个相等的区间点$x=h,x-2h,\ldots,x=nh$上的值，对于同样位置处的真是解$u$我们计算近似解$u_1,\ldots,u_n$，在端点处$x=0,x=1=(n+1)h$处，边界值是$u_0=0,u_{n+1}=0$。

第一个问题是：我们如何替换导数$d^2u/dx^2$？一阶导数可以近似表示为有限步长内停止的$\Delta u/\Delta x$并且不允许$h(or\Delta x)$趋近于零，$\Delta u$可以是前面的，后面的或中间的：

$$\begin{equation} \frac{\Delta u}{\Delta x}=\frac{u(x+h)-u(x)}{h}\ or\ \frac{u(x)-u(x-h)}{h}\ or\ \frac{u(x+h)-u(x-h)}{2h}\tag3 \end{equation}$$

最后一个关于$x$对称，它是最精确的。对于二阶导数，只是利用$x,x\pm h$处数值的一个组合：

$$\begin{equation} \frac{d^2u}{dx^2}\approx\frac{\Delta ^2u}{\Delta x^2}=\frac{u(x+h)-2u(x)+u(x-h)}{h^2}\tag4 \end{equation}$$

它也有关于$x$对称的优点。重复一遍：当$h\to \infty$时右边接近$d^u/dx^2$ 的真实值，但是我们必须让$h$停在某个正数上。

对每个点$x=jh$，方程$-d^2u/dx^2=f(x)$可以用它的离散模拟(5)代替，我们通过乘以$h^2$来得出$n$个方程$Au=b$：

$$\begin{equation} -u_{j+1}+2u_{j}-u_{j-1}=h^2f(jh)\quad for\ j=1,\ldots,n\tag5 \end{equation}$$

第一个和最后一个($j=1,j=n$)包含$u_0=0,u_{n+1}=0$，他们是已知的边界条件，如果这些值非零的话，他们就转化成右边的值。这$n$个方程(5)的结构可以更矩阵形式来更好的可视化，我们选择$h=\frac{1}{6}$，从而得到$5\times 5$ 的矩阵：

$$\begin{equation} \begin{bmatrix} 2&-1&&&\\-1&2&-1&&\\&-1&2&-1&\\&&-1&2&-1\\&&&-1&2 \end{bmatrix} \begin{bmatrix} u_1\\u_2\\u_3\\u_4\\u_5 \end{bmatrix} =h^2\begin{bmatrix} f(h)\\f(2h)\\f(3h)\\f(4h)\\f(5h) \end{bmatrix}\tag6 \end{equation}$$

现在，我们将求解方程(6)，它的系数矩阵非常有规律，有许多特殊的性质，其中有三个是非常基本的：

1. 矩阵$A$是三对角的。所有非零元素位于主对角线以及附近的两条对角线上，这条窄带以外的$a_{ij}=0$，这些零大大简化了高斯消元过程。
2. 矩阵是对称的。每个元素$a_{ij}$等于它的镜像$a_{ji}$，使得$A^{T}=A$。上三角矩阵$U$将是下三角矩阵$L$的转置，$A=LDL^{T}$。$A$的对称性反映了$d^2u/dx^2$的对称性，奇导数像$du/dx,d^3u/dx^3$将破坏对称性。
3. 矩阵是正定的。这个额外的性质说明主元是正的，在理论和实践中不需要行变换。这和本文末尾要将的矩阵$B$(非正定的)正好相反，在没有行变换的情况下，它将对舍入非常敏感。另外关于正定的概念我会在以后的文章中详细介绍！

我们返回到$A$是三对角矩阵这个事实，它对消元会有什么影响呢？消元过程的第一步是在第一个主元下面产生零：

$$\begin{bmatrix} 2&-1&&&\\-1&2&-1&&\\&-1&2&-1&\\&&-1&2&-1\\&&&-1&2 \end{bmatrix} \to \begin{bmatrix} 2&-1&&&\\0&\frac{3}{2}&-1&&\\&-1&2&-1&\\&&-1&2&-1\\&&&-1&2 \end{bmatrix}$$

跟一般的$5\times 5$矩阵相比，这一步主要有两个简化：

1. 在主元下面只有一个非零元素
2. 主元所在的行非常短

乘数因子是$\ell=-\frac{1}{2}$，新的主元是$\frac{3}{2}$。更进一步，三对角模式保留着：每步消元都允许这两个简化。

最终结果是$LDU=LDL^{T}$，注意主元！

$$A= \begin{bmatrix} 1&&&&\\-\frac{1}{2}&1&&&\\&-\frac{2}{3}&1&&\\&&-\frac{3}{4}&1&\\&&&-\frac{4}{5}&1 \end{bmatrix} \begin{bmatrix} \frac{2}{1}&&&&\\&\frac{3}{2}&&&\\&&\frac{4}{3}&&\\&&&\frac{5}{4}&\\&&&&\frac{6}{5} \end{bmatrix} \begin{bmatrix} 1&-\frac{1}{2}&&&\\&1&-\frac{2}{3}&&\\&&1&-\frac{3}{4}&\\&&&1&-\frac{4}{5}\\&&&&1 \end{bmatrix}$$

三对角矩阵的$L,U$分解因子是二对角矩阵，三个因子和矩阵$A$一样对角线有同样的带状结构，注意$L,U$互相之间存在转置关系，我们从对称就预期到会如此，主元$2/1,3/2,4/3,5/4,6/5$都是正的，他们的乘积就是$A$的行列式$detA=6$。当$n$不断变大时，这些主元明显收敛到1，这样的矩阵计算起来非常方便。

稀疏因子$L,U$完全改变了通常的操作次数，每列的消元只需要两步，对于$n$列来说，次数从$n^3/3$降到了$2n$，三对角方程组几乎能很快解决，求解它的代价和$n$成正比。

带状矩阵就是在$|i-j|<w$内$a_{ij}=0$(图1)，对角矩阵的半个带宽$w=1$，三对角矩阵的为$w=2$,，当$w=n$时就是就是一般的矩阵了。对每一列，消元法需要$w(w-1)$次操作：长为$w$的行对下面的$w-1$行进行操作，对于$n$列的带状矩阵大约需要$w^2n$次操作。

当$w$趋近$n$时，矩阵变成一般矩阵，次数变成$n^3$。产生$L,D,U$的除法和乘-减(不考虑$A$为对称这个假设)精确次数是$P=\frac{1}{3}w(w-1)(3n-2w+1)$，对于一般矩阵即$w=n$，$P=\frac{1}{3}n(n-1)(n+1)$，这是一个整数，因为$n-1,n,n+1$是连贯的，所以他们之中有一个能被3整除。

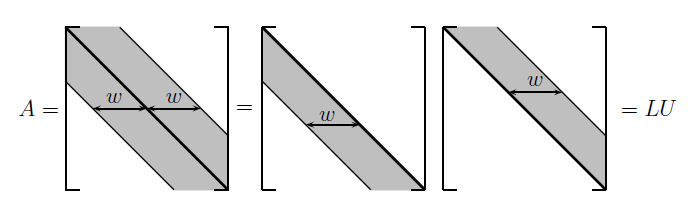
图1：带状矩阵 $A$和它的因子$L,U$

这是我们最终得到的操作次数，我们强调一点，像$A$那样的有限差分矩阵有逆，在求解$Ax=b$时，知道$A^{-1}$比知道$L,U$要糟糕，因为$A^{-1}$乘$b$需要$n^2$步，而前向消元和回代(产生$x=U^{-1}c=U^{-1}L^{-1}b=A^{-1}b$)$4n$ 步就足够了。

我们希望本例增强读者对消元的理解，它是实践中遇到的一个大型线性方程实例，接下来对于$n$个未知量的$m$个方程，我们将转向讨论$x$的存在性和唯一性。

舍入误差

理论上非奇异情况有完整的主元(考虑行变换)，实践中，需要更多的行交换否则计算的解可能变得毫无价值。接下来我们重点来讲如何使消元更加稳定-为什么需要它以及如何做。

对于中等大小的系统，比如说$100\times 100$，消元可能涉及一百万的三分之一次($\frac{1}{3}n^3$)，对于每步操作，我们必须预期舍入误差。通常情况下，我们固定有效位数，然后将两个大小不同的数相加给出一个误差：

$$.456+.00123\to .457\quad \text{丢掉数字2和3}$$

那么所有这些误差是如何影响$Ax=b$的最终误差的呢？

这不是一个简单的问题。而这个问题被约翰$\cdot$冯$\cdot$ 诺依曼碰到了，在计算机使得100万步操作成为可能的时候，是他引领了数学。事实上高斯和冯$\cdot$诺依曼的结合给出了简单的消元算法，虽然冯诺依曼高估了最后的舍入误差。威尔金森(Wilkinson)找到这个问题的正确方法，并且他的书到现在依然是经典。

我们将给出两个简单的例子来说明舍入误差的重要性：

$$A= \begin{bmatrix} 1.&1.\\1.&1.0001 \end{bmatrix} \qquad B= \begin{bmatrix} .001&1.\\1.&1. \end{bmatrix}$$

$A$几乎是奇异的而$B$离奇异很远，如果我们稍微将$A$中的元素改一下$a_{22}=1$，它既是奇异的。考虑两个非常接近的向量$b$：

$$ill-conditioned\ \begin{matrix} u&+&v&=&2\\u&+&1.0001v&=&2 \end{matrix} \quad and\quad well-conditioned\ \begin{matrix} u&+&v&=&2\\u&+&1.0001v&=&2.0001 \end{matrix}$$

第一个解是$u=2,v=0$，而第二个解是$u=v=1$。$b$中第五位数的改变放大到解中第一位数的改变，没有任何数值方法可以避免它对小扰动这种敏感，病态条件能够从一个地方转到另一个地方，但是无法移除。真实解都如此敏感更别说计算解了。

第二点如下：

15、即便是一个$well-conditioned$矩阵$B$也可能别差的算法个毁掉

我们很遗憾的说：对于矩阵$B$，直接使用高斯消元就是一种差的算法。假设.0001作为第一个主元，那么第二行需要减去第一行的10000倍，右下角就变成了-9999，但是第三位四舍五入将变为-10000，为1的元素将会消失：

$$\begin{matrix} .0001u+v&=&2\\u+v&=&2 \end{matrix} \to \begin{matrix} .0001u+v&=&1\\-9999v&=&-9998 \end{matrix}$$

四舍五入将得到$-10000v=-10000$或者$v=1$。首先我们用正确值$v=.999$(保留三位小数)回代将得到$u=1$：

$$.0001u+.9999=1\quad or\quad u=1$$

但是如果接受$v=1$，我们将得到$u=0$：

$$.0001u+1=1\quad or\quad u=0$$

计算结果完全不对，$B$是well-conditioned但是消元明显不稳定，$L,D,U$也明显是比$B$大许多：

$$B= \begin{bmatrix} 1&0\\10000&1 \end{bmatrix} \begin{bmatrix} .0001&0\\0&-9999 \end{bmatrix} \begin{bmatrix} 1&10000\\0&1 \end{bmatrix}$$

小主元.0001带来了不稳定，补救方法很明显-换行

16、一个小主元迫使消元中发生变化。通常我们比较同一列所有可能的主元，将最大主元换到当前的位置

对于$B$来讲，.0001将和下面的1比较，立马进行行交换，从矩阵的角度来讲就是乘以一个置换矩阵$P$，新矩阵$C=PB$就有好的因子：

$$C=\begin{bmatrix} 1&1\\.0001&1 \end{bmatrix}= \begin{bmatrix} 1&0\\.0001&1 \end{bmatrix} \begin{bmatrix} 1&0\\0&.9999 \end{bmatrix} \begin{bmatrix} 1&1\\0&1 \end{bmatrix} \qquad P= \begin{bmatrix} 0&1\\1&0 \end{bmatrix}$$

$C$的主元是1和.9999，比$B$的.0001和-9999要好。

还有一种策略就是与其余所有列中最大主元进行交换，这时候可能不仅是行，也会有列交换。(这时候置换矩阵乘在右边)这么做的代价太高，上面的方法其实已经够了。

我们说完了数值线性代数的基本算法：带有行变换的消元法。一些进一步的完善，比如看整行或列，都是有可能的，但本质上读者现在知道了一台电脑如何解线性方程组，相比“理论”描述-找到$A^{-1}$并相乘$A^{-1}b$-我们的描述已花费了大量时间和耐心，我希望能够用更简单的方法来解释 x <script type="math/tex" id="MathJax-Element-7260">x</script>是如何发现的，但是我认为我还没有找到。(博主心声：期待大家能有更好的方法提出来)