自动控制原理
控制系统(Control system):在给定的条件下,通过操纵达到预期性能的系统
控制系统中的操纵器:控制器(contriller)/补偿器(compensator)[重点在于控制参数与结构]
控制器需要考虑的三大性能
- 稳定性(Stability):有界输入对应有界输出(BIBO)
- 瞬时响应(Transient response):指标:响应速度
- 稳态响应(Steady-state response)
控制目标:
- 稳定不稳定的系统
- 提高系统的稳定性;使得系统具有更好的稳定性。等效于改善系统的瞬时响应:更快的响应,较小的超调量,减小振荡
- 精准跟踪输入命令:减少/消除特定类型输入的稳态误差
判断微分方程,线性或非线性,时变或定长
是否为线性:如果每一项都是c(t),r(t),高阶导数,则为线性。但是如果出现平方线与单常数x则为非线性。
时变与非时变:c(t),r(t)的系数全是常数,不存在变量t
传递方程(transfer function)
a n d n c ( t ) d t n + a n − 1 d n − 1 c ( t ) d t n − 1 + ⋯ + a 0 c ( t ) = b m d m r ( t ) d t m + b m − 1 d m − 1 r ( t ) d t m − 1 + ⋯ + b 0 r ( t ) a_{n}\frac{d^{n}c(t)}{dt^{n}}+a_{n-1}\frac{d^{n-1}c(t)}{dt^{n-1}}+\cdots+a_{0}c(t)=b_{m}\frac{d^{m}r(t)}{dt^{m}}+b_{m-1}\frac{d^{m-1}r(t)}{dt^{m-1}}+\cdots+b_{0}r(t) andtndnc(t)+an−1dtn−1dn−1c(t)+⋯+a0c(t)=bmdtmdmr(t)+bm−1dtm−1dm−1r(t)+⋯+b0r(t)
左右两边分别进行拉氏变换,我们假设其初始状态为0可得:
(
a
n
s
n
+
a
n
−
1
s
n
−
1
+
⋯
+
a
0
)
C
(
s
)
=
(
b
m
s
m
+
b
m
−
1
s
m
−
1
+
⋯
+
b
0
)
R
(
s
)
(a_ns^n+a_{n-1}s^{n-1}+\cdots+a_0)C(s)=(b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0)R(s)
(ansn+an−1sn−1+⋯+a0)C(s)=(bmsm+bm−1sm−1+⋯+b0)R(s)
C ( s ) R ( s ) = G ( s ) = ( b m s m + b m − 1 s m − 1 + ⋯ + b 0 ) ( a n s n + a n − 1 s n − 1 + ⋯ + a 0 ) \frac{C(s)}{R(s)}=G(s)=\frac{(b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0)}{(a_ns^n+a_{n-1}s^{n-1}+\cdots+a_0)} R(s)C(s)=G(s)=(ansn+an−1sn−1+⋯+a0)(bmsm+bm−1sm−1+⋯+b0)

解题步骤:
-
Replace passive element values with their impedances.
-
Replace all sources and time variables with their Laplace transform.
-
Assume a transform current and a current direction in each mesh.
-
Write Kirchhoff’s voltage law around each mesh.
-
Solve the simultaneous equations for the output.
-
Form the transfer function
-
将无源元件值替换为其阻抗。
-
将所有源和时间变量替换为其拉普拉斯变换。
-
假设每个网格中存在变换电流和当前方向。
-
在每个网格周围写出基尔霍夫电压定律。
-
求解联立方程以获得输出。
-
形成传递函数
例题如下:
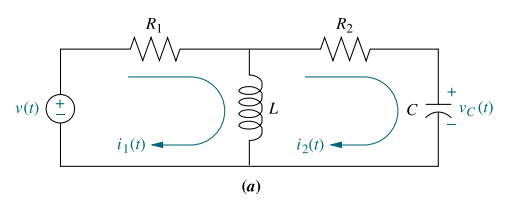
寻找其传递方程 I 2 ( s ) / V ( s ) {I_2(s)/V(s)} I2(s)/V(s)
-
将无源元件值替换为其阻抗,并进行拉氏变换同时设定好电流在网格中的流动方向。

-
在每个网格周围写出基尔霍夫电压定律。
KaTeX parse error: Expected 'EOF', got '&' at position 16: (R_1+Ls)I_1(s)&̲-LsI_2(s)=V(s)\… -
求解联立方程以获得输出。(一般情况下使用克莱姆法则)
I 2 ( s ) = ∣ ( R 1 + L s ) V ( s ) − L s 0 ∣ Δ = L s V ( s ) Δ I_{2}(s)=\frac{\left|\begin{array}{cc} \left(R_{1}+L s\right) & V(s) \\ -L s & 0 \end{array}\right|}{\Delta}=\frac{L s V(s)}{\Delta} I2(s)=Δ (R1+Ls)−LsV(s)0 =ΔLsV(s)Δ = ∣ ( R 1 + L s ) − L s − L s ( L s + R 2 + 1 C s ) ∣ \left.\Delta=\left|\begin{matrix}(R_1+Ls)&-Ls\\\\-Ls&\left(Ls+R_2+\frac{1}{Cs}\right)\end{matrix}\right.\right| Δ= (R1+Ls)−Ls−Ls(Ls+R2+Cs1)
-
整理可得传递方程为
G ( s ) = I 2 ( s ) V ( s ) = L s Δ = L C s 2 ( R 1 + R 2 ) L C s 2 + ( R 1 R 2 C + L ) s + R 1 G(s)=\frac{I_{2}(s)}{V(s)}=\frac{Ls}{\Delta}=\frac{LCs^{2}}{(R_{1}+R_{2})LCs^{2}+(R_{1}R_{2}C+L)s+R_{1}} G(s)=V(s)I2(s)=ΔLs=(R1+R2)LCs2+(R1R2C+L)s+R1LCs2
利用拉普拉斯变换解微分方程的步骤如下:
①对方程两侧同时进行拉普拉斯变换,其中的F(s)就是我们要求的原函数经过拉普拉斯变换的结果;
②带入初值条件;
③把要求的原函数F(s)用关于s的表达式g(s)表达;
④对③中得到的F(s)=g(s)两侧进行拉普拉斯逆变换即可得到微分方程的解。
微分的拉式变换
一次微分 L [ f ′ ( t ) ] = s F ( s ) − f ( 0 ) L[f'(t)]=sF(s)-f(0) L[f′(t)]=sF(s)−f(0)
二次微分 L [ f ′ ′ ( t ) ] = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 ) L[f''(t)]=s^2F(s)-sf(0)-f'(0) L[f′′(t)]=s2F(s)−sf(0)−f′(0)
三次微分
L
[
f
′
′
′
(
t
)
]
=
s
3
F
(
s
)
−
s
2
f
(
0
)
−
s
f
′
(
0
)
−
f
′
′
(
0
)
L[f'''(t)]=s^3F(s)-s^2f(0)-sf'(0)-f''(0)
L[f′′′(t)]=s3F(s)−s2f(0)−sf′(0)−f′′(0)
L
[
f
′
(
t
)
]
=
∫
0
∞
e
−
s
t
[
e
a
t
f
(
t
)
]
d
t
=
e
−
s
t
f
(
t
)
∣
L
0
+
s
∫
0
∞
e
−
s
t
f
(
t
)
d
t
=
s
F
(
s
)
=
f
(
0
)
L[f^{\prime}(t)]=\int_{0}^{\infty}e^{-s t}[e^{a t}f(t)]d t=e^{-s t}f(t)|\begin{array}{c}{{L}}\\ {{0}}\end{array}+s\int_{0}^{\infty}e^{-s t}f(t)d t=s F(s)=f(0)
L[f′(t)]=∫0∞e−st[eatf(t)]dt=e−stf(t)∣L0+s∫0∞e−stf(t)dt=sF(s)=f(0)
直线机械系统的传递函数(Translational Mechanical System)

旋转机械系统的传递函数(Rotational Mechanical System)

梅森公式
计算任意输入节点到输出节点的传递函数的梅森增益公式为:
P
=
1
Δ
∑
k
=
1
n
P
k
Δ
k
P=\frac{1}{\Delta}\sum_{k=1}^{n}P_{k}\Delta_{k}
P=Δ1k=1∑nPkΔk
其中
Δ
\Delta
Δ为系统的特征多项式,其计算公式为:
Δ
=
1
−
∑
L
a
+
∑
L
b
L
c
−
∑
L
d
L
e
L
f
+
⋯
\Delta=1-\sum L_a+\sum L_bL_c-\sum L_dL_eL_f+\cdots
Δ=1−∑La+∑LbLc−∑LdLeLf+⋯
其中:
∑ L a \sum L_a ∑La为所有不同回路增益之和;
∑ L b L c \sum L_bL_c ∑LbLc为所有两两不接触回路增益之和;
∑ L d L e L f + ⋯ \sum L_dL_eL_f+\cdots ∑LdLeLf+⋯ 为所有互不接触的回路中,每次取其中三个回路的增益乘积之和;
后面的以此类推。n为从输入节点到输出节点的前向通路条数
P
k
P_k
Pk 为从输入节点到输出节点的第k条前向通路的总增益;
Δ
k
\Delta_{k}
Δk 为第k条前向通路的余子式,即把特征式
Δ
\Delta
Δ中与该前向通道相接触的回路增益置零后剩余的部分。
在做题中一共分为4步:
-
先找出所有的闭环回路,即为 ∑ L a \sum L_a ∑La,再找出两两不相邻回路,即为 ∑ L b L c \sum L_bL_c ∑LbLc,依次类推直到找全,求出整个系统的特征式
-
接着找出系统的前向通路,即为$ \sum P_{k}$
-
找到每一项的余子式,各回路均与前向通路如果有接触,其余子式为1;如果相互没有接触
,其余子式为 1 − 其闭环回路 1-其闭环回路 1−其闭环回路 -
带入即可求得其传递函数
一阶系统分析
一阶系统的传递函数标准形式为: G ( s ) = C ( s ) R ( s ) = 1 T s + 1 G(s)=\frac{C(s)}{R(s)}=\frac{1}{Ts+1} G(s)=R(s)C(s)=Ts+11
以输入信号为单位脉冲响应举例,单位脉冲信号的拉式变换为1,即 R ( s ) = 1 R(s)=1 R(s)=1其拉氏变换应为其自身的拉式变换。化简s的系数为1可得: G ( s ) = 1 T s + 1 = 1 T ⋅ 1 s + 1 / T G(s)=\frac{1}{Ts+1}=\frac{1}{T}\cdot\frac{1}{s+1/T} G(s)=Ts+11=T1⋅s+1/T1
进行拉氏变换: c ( t ) = L ′ [ G ( s ) ] = 1 T ⋅ e − 1 T ′ c(t)=\mathscr{L}^{\prime}\bigl[G(s)\bigr]=\frac{1}{T}\cdot\mathrm{e}^{-\frac{1}{T}\prime} c(t)=L′[G(s)]=T1⋅e−T1′
有例题如下:
根据框图可以求得其传递函数为: C ( s ) R ( s ) = K h G ( s ) 1 + K f G ( s ) = 10 K h 1 + 10 K f ⋅ 1 0.2 1 + 10 K f s + 1 \frac{C(s)}{R(s)}=\frac{K_{h}G(s)}{1+K_{f}G(s)}=\frac{10K_{h}}{1+10K_{f}}\cdot\frac{1}{\frac{0.2}{1+10K_{f}}s+1} R(s)C(s)=1+KfG(s)KhG(s)=1+10Kf10Kh⋅1+10Kf0.2s+11
改变题目给定的传递时间由0.2变为0.02
可得: 10 K h 1 + 10 K f ⋅ 1 0.2 1 + 10 K f s + 1 = 10 0.02 s + 1 \frac{10K_\mathrm{h}}{1+10K_\mathrm{f}}\cdot\frac1{\frac{0.2}{1+10K_\mathrm{f}}s+1}=\frac{10}{0.02s+1} 1+10Kf10Kh⋅1+10Kf0.2s+11=0.02s+110
列式可得: { 10 K h 1 + 10 K f = 10 0.2 1 + 10 K f = 0.02 \left.\left\{\begin{array}{cc}\frac{10K_\mathrm{h}}{1+10K_\mathrm{f}}=10\\\\\frac{0.2}{1+10K_\mathrm{f}}=0.02\\\end{array}\right.\right. ⎩ ⎨ ⎧1+10Kf10Kh=101+10Kf0.2=0.02
解: K f = 0.9 , K h = 10 K_{f}=0.9,K_{h}=10 Kf=0.9,Kh=10
劳斯判据
可以根据闭环传递函数的特征方程如下表格对应写拉斯表



举例:

由于第一列的系数不全为正,因此系统不稳定。
例题:
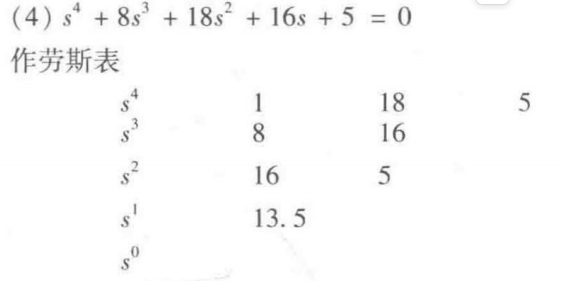
由于第一列的系数都大于零,所以该系统稳定。
劳斯判据中的特殊情况
(1)在计算中,第一列有零出现。
出现这种情况时,可以用一个很小的正数代替,继续完成计算。如果第一列中的元素除了出现的零值外,其余全部大于零,则说明系统有临界稳定的特征根。
(2)第一列的系数出现变号:改变符号(正负相互转化)的次数,即不稳定根的个数。
举例: s 3 − 3 s + 2 = 0 s^{3}-3s+2=0 s3−3s+2=0
其劳斯表为:
这个变号的次数即为不稳定跟的个数。
(3)出现零行(即劳斯表的每一行都是0),则存在大小相等,方向相反的根。
s 5 + 2 s 4 + 24 s 3 + 48 s 2 − 25 s − 50 = 0 s^{5}+2s^{4}+24s^{3}+48s^{2}-25s-50=0 s5+2s4+24s3+48s2−25s−50=0
劳斯表计算中出现零行时,可用零行的前一行作辅助多项式
P
(
s
)
P(s)
P(s),然后由
d
P
(
s
)
d
s
\frac{dP(s)}{ds}
dsdP(s)的系数行代替零行,完成劳斯表的计算,如下面例题所示。


例题:
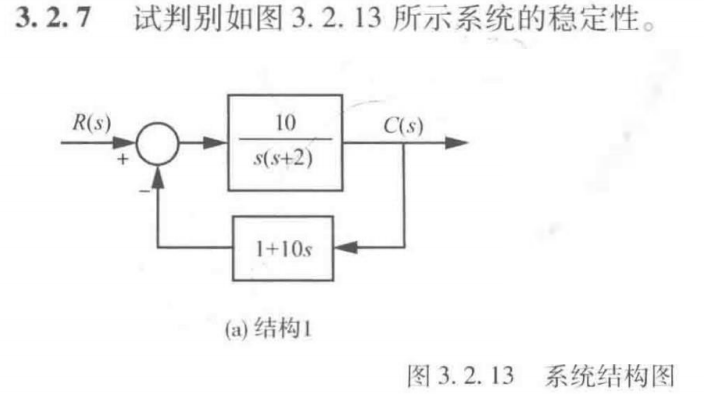
根据框图可以得到其闭环传递函数为: G c ( s ) = 10 s ( s + 2 ) 1 + ( 1 + 10 s ) 10 s ( s + 2 ) = 10 s 2 + 102 s + 10 G_c(s)=\frac{\frac{10}{s(s+2)}}{1+(1+10s)\frac{10}{s(s+2)}}=\frac{10}{s^2+102s+10} Gc(s)=1+(1+10s)s(s+2)10s(s+2)10=s2+102s+1010
闭环特征方程为: s 2 + 102 s + 10 = 0 s^2+102s+10=0 s2+102s+10=0
据此列劳斯表易,其系数全部为正,即方程稳定。
二阶系统分析
二阶系统的结构图如下:
其开环传递函数为:
G
o
(
s
)
=
ω
n
2
s
(
s
+
2
ζ
ω
n
)
G_{_{o}}(s)=\frac{\omega_{n}^{2}}{s(s+2\zeta\omega_{_{n}})}
Go(s)=s(s+2ζωn)ωn2
闭环传递函数为:
G
c
(
s
)
=
ω
n
2
s
2
+
2
ζ
ω
n
s
+
ω
n
2
G_{c}(s)=\frac{\omega_{n}^{2}}{s^{2}+2\zeta\omega_{n}s+\omega_{n}^{2}}
Gc(s)=s2+2ζωns+ωn2ωn2
闭环传递函数的分母多项式等于零的代数方程称为二阶系统的闭环特征方程,即:
s
2
+
2
ζ
ω
n
s
+
ω
n
2
=
0
s^{2}+2\zeta\omega_{_n}s+\omega_{_n}^{2}=0
s2+2ζωns+ωn2=0
闭环特征方程的两个根称为二阶系统的特征根,即
s
1
,
2
=
−
ζ
ω
n
±
ω
n
ζ
2
−
1
s_{_{1,2}}=-\zeta\omega_{_n}\pm\omega_{_n}\sqrt{\zeta^{2}-1}
s1,2=−ζωn±ωnζ2−1
| 符号 | 名称 | 量纲 |
|---|---|---|
| ζ \zeta ζ | 二阶系统的阻尼比 | 1 |
| $ \omega_{n }$ | 无阻尼振荡频率 | rad/s |
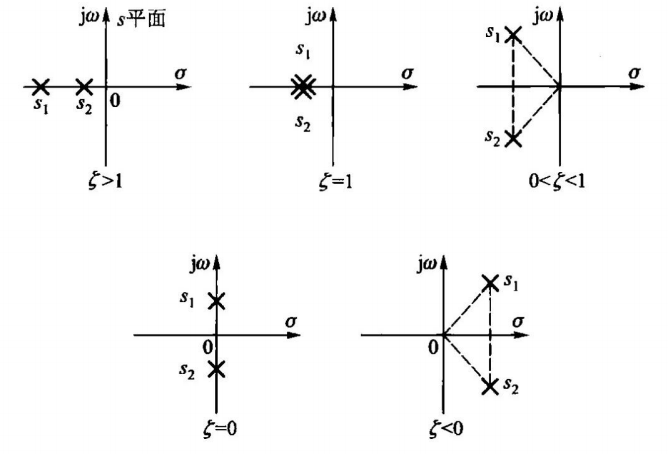
根据 ζ \zeta ζ的值范围的不同,一共有如下物种情况:
| 范围 | 特征根位置 | 系统响应情况 |
|---|---|---|
| ζ > 1 \zeta > 1 ζ>1 | 特征根为一对不相等的负实根,位于s平面的负实轴上 | 过阻尼 |
| ζ = 1 \zeta = 1 ζ=1 | 特征根为一对相等的负实根;也是位于s平面的负实轴上 | 临界阻尼 |
| 0 < ζ < 1 0< \zeta <1 0<ζ<1 | 特征根为一对带有负实部的共钜复数根,位于s平面的左半平面上 | 欠阻尼 |
| ζ = 0 \zeta = 0 ζ=0 | 特征根为一对纯虚根,位于s平面的虚轴上 | 无阻尼 |
| ζ < 0 \zeta < 0 ζ<0 | 特征根位于s平面的右半平面上 | 发散 |
二阶系统的性能指标计算
| 符号 | 名称 | 计算式 |
|---|---|---|
| ω d \omega_{\mathrm{d}} ωd | 阻尼振荡频率(rad/s) | ω d = ω n 1 − ξ 2 \omega_{\mathrm{d}}=\omega_{_n}\sqrt{1-\xi^{2}} ωd=ωn1−ξ2 |
| t r t_r tr | 上升时间 | t r = π − β ω d t_{_r}=\frac{\pi-\beta}{\omega_{_\mathrm{d}}} tr=ωdπ−β |
| t p t_p tp | 峰值时间 | t p = π ω d t_{_p}=\frac{\pi}{\omega_{_d}} tp=ωdπ |
| M p M_p Mp | 超调量 | M p = e − ζ 1 − ζ 2 π × 100 % M_p=\mathrm{e}^{-\frac\zeta{\sqrt{1-\zeta^2}}\pi}\times100\% Mp=e−1−ζ2ζπ×100% |
依照一阶系统调节时间的计算公式可以近似估算二阶欠阻尼系统的调节时间为:
t s = 3 T = 3 ζ ω n , ± 5 % 误差带宽度时 t_{_s}=3T={\frac{3}{\zeta\omega_{_n}}},\pm5\%\text{误差带宽度时} ts=3T=ζωn3,±5%误差带宽度时
t s = 4 T = 4 ζ ω n , ± 2 % 误差带宽度时 t_{_s}=4T=\frac{4}{\zeta\omega_{_n}},\pm2\%\text{误差带宽度时} ts=4T=ζωn4,±2%误差带宽度时
有例题如下:
根据框图易得其开环传递函数如下:
G
o
(
s
)
=
5
K
s
(
s
+
34.5
)
G_{_o}(s)=\frac{5K}{s(s+34.5)}
Go(s)=s(s+34.5)5K
(1)闭环传递函数:
G
c
(
s
)
=
G
s
(
s
)
1
+
G
s
(
s
)
=
5
K
s
(
s
+
34.5
)
1
+
5
K
s
(
s
+
34.5
)
=
5
K
s
2
+
34.5
s
+
5
K
=
1
s
2
+
34.5
s
+
1000
G_{_c}(s)=\frac{G_{_s}(s)}{1+G_{_s}(s)}=\frac{\frac{5K}{s(s+34.5)}}{1+\frac{5K}{s(s+34.5)}}=\frac{5K}{s^{2}+34.5s+5K}=\frac{1}{s^{2}+34.5s+1000}
Gc(s)=1+Gs(s)Gs(s)=1+s(s+34.5)5Ks(s+34.5)5K=s2+34.5s+5K5K=s2+34.5s+10001
带入标准二阶传递函数形式,可得特征根参数:
G
c
(
s
)
=
1
s
2
+
34.5
s
+
1000
=
ω
n
2
s
2
+
2
ζ
ω
n
s
+
ω
n
2
G_{\mathrm{c}}(s)=\frac{1}{s^{2}+34.5s+1000}=\frac{\omega_{n}^{2}}{s^{2}+2\zeta\omega_{n}s+\omega_{n}^{2}}
Gc(s)=s2+34.5s+10001=s2+2ζωns+ωn2ωn2
2 ζ ω n = 34.5 , ω n 2 = 1000 ω n = 31.6 r a d / s ζ = 0.545 \begin{gathered} 2\zeta\omega_{n}=34.5,\omega_{n}^{2}=1000 \\ \omega_{n}=31.6\mathrm{rad/s} \\ \zeta=0.545 \end{gathered} 2ζωn=34.5,ωn2=1000ωn=31.6rad/sζ=0.545
峰值时间: t p = π ω d = π ω n 1 − ζ 2 = 0.12 s t_{_p}=\frac{\pi}{\omega_{_d}}=\frac{\pi}{\omega_{_n}\sqrt{1-\zeta^{^2}}}=0.12\mathrm{s} tp=ωdπ=ωn1−ζ2π=0.12s
超调量: M p = e − ζ 1 − ζ 2 π × 100 % = 0.13 × 100 % = 13 % M_{_p}=\mathrm{e}^{-\frac{\zeta}{\sqrt{1-\zeta^{2}}}\pi}\times100\%=0.13\times100\%=13\% Mp=e−1−ζ2ζπ×100%=0.13×100%=13%
调节时间: t s = 3 ζ ω n = 0.17 s ( ± 5 % ) t s = 4 ζ ω n = 0.23 s ( ± 2 % ) \begin{aligned}t_{s}&=\frac{3}{\zeta\omega_{n}}=0.17\mathrm{s}(\pm5\%)\\t_{s}&=\frac{4}{\zeta\omega_{n}}=0.23\mathrm{s}(\pm2\%)\end{aligned} tsts=ζωn3=0.17s(±5%)=ζωn4=0.23s(±2%)
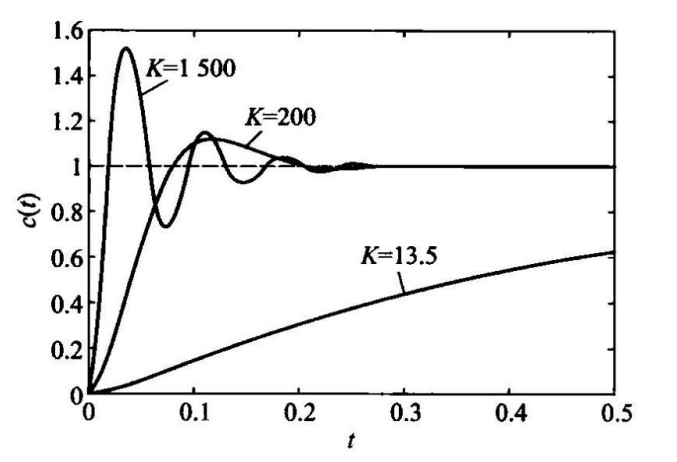
(2)讨论K=1500和K=13.5时,对系统动态性能的影响。
当K=1500时,闭环传递函数为: G c ( s ) = 5 K s 2 + 34.5 s + 5 K = 7500 s 2 + 34.5 s + 7500 G_{_{c}}(s)=\frac{5K}{s^{2}+34.5s+5K}=\frac{7500}{s^{2}+34.5s+7500} Gc(s)=s2+34.5s+5K5K=s2+34.5s+75007500
特征参数: ω n = 86.6 r a d / s , ζ = 0.2 \omega_{n}=86.6\mathrm{rad/s},\zeta=0.2 ωn=86.6rad/s,ζ=0.2
性能指标: t p = 0.037 s , M p = 52.7 % , t s = 0.17 s t_{_p}=0.037s,M_{_p}=52.7\%,t_{_s}=0.17s tp=0.037s,Mp=52.7%,ts=0.17s
可得其阻尼振荡频率: ω d = ω n 1 − ζ 2 = 86.6 1 − 0. 2 2 r a d / s = 84.85 r a d / s \omega_{\mathrm{d}}=\omega_{\mathrm{n}}\sqrt{1-\zeta^{2}}=86.6\sqrt{1-0.2^{2}}\mathrm{rad/s=84.85rad/s} ωd=ωn1−ζ2=86.61−0.22rad/s=84.85rad/s
当K=13.5时,闭环传递函数为:
G c ( s ) = 5 K s 2 + 34.5 s + 5 K = 67.5 s 2 + 34.5 s + 67.5 G_{\mathrm{c}}(s)=\frac{5K}{s^{2}+34.5s+5K}=\frac{67.5}{s^{2}+34.5s+67.5} Gc(s)=s2+34.5s+5K5K=s2+34.5s+67.567.5
对应特征参数为: ω n = 8.22 r a d / s \omega_{_n}=8.22\mathrm{rad/s} ωn=8.22rad/s
ζ = 2.1 \zeta=2.1 ζ=2.1
此时,系统为过阻尼的,没有超调量,曲线上升很慢。由近似计算可求得调节时间为: t s ≈ 3 T 1 = 1.44 s t_{s}\approx3T_{1}=1.44\mathrm{s} ts≈3T1=1.44s
过阻尼情况下的调节时间
过阻尼系统的阻尼系数比: ζ > 1 \zeta>1 ζ>1
特征根为两个不相等的负实根: s 1 , 2 = − ζ ω n ± ω n ζ 2 − 1 s_{_{1,2}}=-\zeta\omega_{_n}\pm\omega_{_n}\sqrt{\zeta^{2}-1} s1,2=−ζωn±ωnζ2−1
闭环传递函数为: G c ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 = 1 T 1 T 2 ( s + 1 T 1 ) ( s + 1 T 2 ) G_{c}\left(s\right)=\frac{\omega_{n}^{2}}{s^{2}+2\zeta\omega_{_{n}}s+\omega_{n}^{2}}=\frac{\frac{1}{T_{1}T_{2}}}{\left(s+\frac{1}{T_{1}}\right)\left(s+\frac{1}{T_{2}}\right)} Gc(s)=s2+2ζωns+ωn2ωn2=(s+T11)(s+T21)T1T21
注意到在时间响应$ c(t) 的表达式中,当 的表达式中,当 的表达式中,当T_2<<T_1 时,因为第三项极快地衰减到零。忽略该项后,时间响应 时,因为第三项极快地衰减到零。忽略该项后,时间响应 时,因为第三项极快地衰减到零。忽略该项后,时间响应c(t)$可以近似为一阶系统的时间响应
c ( t ) ≈ 1 − e − 1 T ′ c(t)\approx1-\mathrm{e}^{-\frac{1}{T}\prime} c(t)≈1−e−T1′
因此,一阶系统的调节时间 t s t_s ts用一阶系统的时间常数T作为参变量表示为:
t s = 3 T , 取误差带宽度为 ± 5 % 时 t_s=3T,\text{取误差带宽度为}\pm5\%\text{时} ts=3T,取误差带宽度为±5%时
t s = 4 T , 取误差带宽度为 ± 2 % 时 t_s=4T,\text{取误差带宽度为}\pm2\%\text{时} ts=4T,取误差带宽度为±2%时
二阶系统响应特性的改善
1.误差信号的比例微分控制(PD控制)
在原典型二阶系统的前向通路上增加误差信号的速度分量并联通路。

2.输出量的速度反馈控制(SF控制)
在原典型二阶系统的反馈通路上增加输出信号的速度分量反馈信号。

例题:
易知上图的闭环传递函数为:
G
c
(
s
)
=
K
s
(
s
+
1
)
1
+
K
s
(
s
+
1
)
(
1
+
K
f
s
)
=
K
s
2
+
(
1
+
K
K
f
)
s
+
K
G_{c}(s)=\frac{\frac{K}{s(s+1)}}{1+\frac{K}{s(s+1)}(1+K_{fs})}=\frac{K}{s^{2}+(1+KK_{f})s+K}
Gc(s)=1+s(s+1)K(1+Kfs)s(s+1)K=s2+(1+KKf)s+KK
比较二阶系统的标准式有:
ω
n
2
=
K
2
ζ
ω
n
=
1
+
K
K
f
\begin{array}{c}{{\omega_{n}^{2}=K}}\\{{2\zeta\omega_{n}=1+KK_{f}}}\\\end{array}
ωn2=K2ζωn=1+KKf
给定的性能指标为:
M
p
=
20
%
,
和
t
p
=
1
s
M_{_p}=20\%,\text{和}t_{_p}=1\mathrm{s}
Mp=20%,和tp=1s
通过:
M
p
=
e
−
ζ
1
−
ζ
2
π
×
100
%
=
20
%
t
p
=
π
ω
d
=
π
ω
n
1
−
ζ
2
=
1
s
\begin{array}{c}{{M_{_p}=\mathrm{e}^{-\frac{\zeta}{\sqrt{1-\zeta^{2}}}\pi}\times100\%=20\%}}\\{{t_{_p}=\frac{\pi}{\omega_{_d}}=\frac{\pi}{\omega_{_n}\sqrt{1-\zeta^{2}}}=1\mathrm{s}}\\}\end{array}
Mp=e−1−ζ2ζπ×100%=20%tp=ωdπ=ωn1−ζ2π=1s解得:
ζ
=
0.456
ω
n
=
3.53
\begin{array}{c}{\zeta=0.456}\\{\omega_{n}=3.53}\\\end{array}
ζ=0.456ωn=3.53
所以: K = ω n 2 = 3.5 3 2 = 12.5 K f = 2 K ζ − 1 K = 0.178 \begin{array}{c}{K=\omega_{n}^{2}=3.53^{2}=12.5}\\{K_{f}=\frac{2\sqrt{K}\zeta-1}{K}=0.178}\\\end{array} K=ωn2=3.532=12.5Kf=K2Kζ−1=0.178
当K=12.5,
K
f
=
0.178
K_f = 0.178
Kf=0.178时,可得:
G
e
(
s
)
=
12.5
s
2
+
s
+
12.5
ξ
=
1
2
K
=
0.14
M
p
=
e
−
ξ
1
−
ϵ
2
π
×
100
%
=
64
%
\begin{aligned}G_{e}(s)&=\frac{12.5}{s^{2}+s+12.5}\\\\\xi&=\frac{1}{2\sqrt{K}}=0.14\\\\\\M_{_p}&=\mathrm{e}^{-\frac{\xi}{\sqrt{1-\epsilon^2}}\pi}\times100\%=64\%\end{aligned}
Ge(s)ξMp=s2+s+12.512.5=2K1=0.14=e−1−ϵ2ξπ×100%=64%
控制系统的稳态误差分析

稳态误差系数类型:
1.当输入为单位阶跃信号时: lim s → 0 G 0 ( s ) \lim_{s\to0}G_{_0}(s) lims→0G0(s)定义为系统的静态位置误差系数 K p K_p Kp,表示为:
K p = lim s → 0 G 0 ( s ) K_{_p}=\operatorname*{lim}_{s\to0}G_{_0}(s) Kp=lims→0G0(s)
其稳态误差: e s s = 1 1 + K p e_{ss}=\frac{1}{1+K_{_p}} ess=1+Kp1
2.当输入为单位斜坡信号时: lim s → 0 G 0 ( s ) \lim_{s\to0}G_{_0}(s) lims→0G0(s)定义为系统的静态位置误差系数 K v K_v Kv,表示为:
K v = lim s → 0 s ⋅ G o ( s ) K_{v}=\lim_{s\rightarrow0}s\cdot G_{_{o}}(s) Kv=lims→0s⋅Go(s)
其稳态误差: e s s = 1 K v e_{ss}=\frac{1}{K_{v}} ess=Kv1
3.当输入为加速度信号时: lim s → 0 G 0 ( s ) \lim_{s\to0}G_{_0}(s) lims→0G0(s)定义为系统的静态位置误差系数 K a K_a Ka,表示为:
K a = lim s → 0 s 2 G 0 ( s ) K_{a}=\lim_{s\rightarrow0}s^{2}G_{_0}(s) Ka=lims→0s2G0(s)
其稳态误差: e s s = 1 K a e_{_{\mathrm{ss}}}=\frac{1}{K_{_{a}}} ess=Ka1

根轨迹法
绘制负反馈系统的9条法则
1.连续性;
2.对称性;
3.根轨迹的分支数;
根轨迹的分支数等于系统的阶数
4.根轨迹的起点和终点;
∏ j = 1 m ( s + z j ) ∏ i = 1 n ( s + p i ) = − 1 K g \frac{\prod_{j=1}^{m}\left(s+z_{j}\right)}{\prod_{i=1}^{n}\left(s+p_{i}\right)}=-\frac{1}{K_{g}} ∏i=1n(s+pi)∏j=1m(s+zj)=−Kg1
当 K g = 0 K_g = 0 Kg=0是根轨迹的起点,分母等于零即为系统的开环极点
当 K g = ∞ K_g = \infty Kg=∞是根轨迹的起点,分子等于零即为系统的开环零点
5.实轴上的根轨迹;
在实轴上选取实验点 s i s_i si,如果实验点 s i s_i si的右方实轴上的开环零点数和极点数的总和为奇数,则实验点 s i s_i si所在的实验段是根轨迹,否则该实验段不是根轨迹。
6.根轨迹的会合点与分离点;
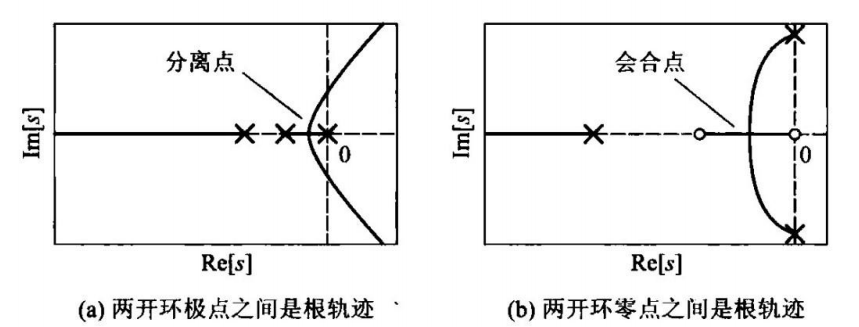
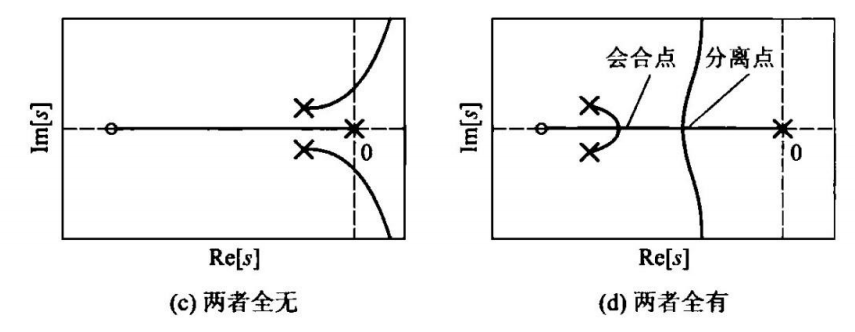
计算分离点或汇合点:
N ′ ( s ) D ( s ) − N ( s ) D ′ ( s ) = 0 N'(s)D(s)-N(s)D'(s)=0 N′(s)D(s)−N(s)D′(s)=0
PS:其中N(s)为变量s的分子多项式,D(s)为变量s的分母多项式。
7.根轨迹的渐近线(与实轴交点;倾斜角)
与实轴交点: − σ = − a n − 1 − b m − 1 n − m = − ∑ i = 1 n p i − ∑ j = 1 m z j n − m -\sigma=-\frac{a_{n-1}-b_{m-1}}{n-m}=-\frac{\sum_{i=1}^{n}p_{i}-\sum_{j=1}^{m}z_{j}}{n-m} −σ=−n−man−1−bm−1=−n−m∑i=1npi−∑j=1mzj
倾斜角: θ = ± 18 0 ∘ ( 2 k + 1 ) n − m \theta=\frac{\pm180^{\circ}(2k+1)}{n-m} θ=n−m±180∘(2k+1)
8.与虚轴交点;
根轨迹可能与虚轴相交,交点坐标的 ω \omega ω 值及相应的 K g K_g Kg值可由劳斯判据求得,也可在特征方程中令s=j ω \omega ω ,然后使特征方程的实部和虚部分别为零求得。
9.出射角与入射角
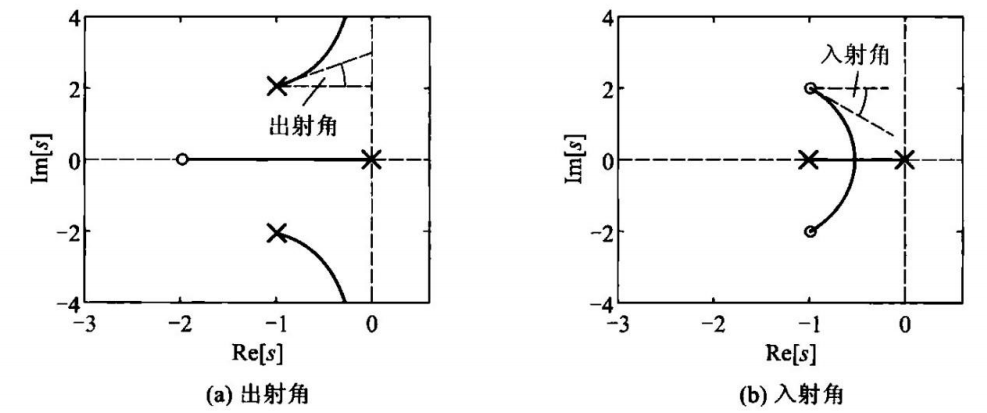
幅角条件为: ∑ j = 1 n arg [ s + z j ] − ∑ i = 1 n arg [ s + p i ] ∣ s = s g = ± 18 0 ∘ ( 2 k + 1 ) \sum_{j=1}^{n}\arg[s+z_{j}]-\sum_{i=1}^{n}\arg[s+p_{i}]\Bigg|_{s = s_g}=\pm180^{\circ}(2k+1) ∑j=1narg[s+zj]−∑i=1narg[s+pi] s=sg=±180∘(2k+1)
令 θ j = arg [ s + z j ] , φ i = arg [ s + p i ] \left.\theta_{j}=\arg\left[\begin{array}{c}{s+z_{j}}\\\end{array}\right.\right],\varphi_{i}=\arg\left[\begin{array}{c}{s+p_{i}}\\\end{array}\right] θj=arg[s+zj],φi=arg[s+pi]
出射角: φ k = ∓ 18 0 ∘ ( 2 k + 1 ) + ∑ j = 1 m θ j − ∑ i = 1 ; i ≠ k n φ i ∣ s = p k \varphi_{k}=\mp180^{\circ}(2k+1)+\sum_{j=1}^{m}\theta_{j}-\sum_{i=1;i\ne k}^{n}\varphi_{i}\Bigg|_{s=p_{k}} φk=∓180∘(2k+1)+∑j=1mθj−∑i=1;i=knφi s=pk
入射角: θ l = ± 18 0 ∘ ( 2 k + 1 ) − ∑ j = 1 j ≠ l m θ j + ∑ i = 1 n φ i ∣ s = z i \theta_{l}=\pm180^{\circ}(2k+1)-\sum_{j=1\atop j\neq l}^{m}\theta_{j}+\sum_{i=1}^{n}\varphi_{i}\Bigg|_{s=z_{i}} θl=±180∘(2k+1)−∑j=lj=1mθj+∑i=1nφi s=zi








 本文围绕自动控制原理展开,介绍了控制系统的概念、控制器性能要求及控制目标。详细阐述传递方程、梅森公式、一阶和二阶系统分析、劳斯判据、根轨迹法等内容,包含各部分的原理、解题步骤及例题,帮助理解自动控制原理的关键知识点。
本文围绕自动控制原理展开,介绍了控制系统的概念、控制器性能要求及控制目标。详细阐述传递方程、梅森公式、一阶和二阶系统分析、劳斯判据、根轨迹法等内容,包含各部分的原理、解题步骤及例题,帮助理解自动控制原理的关键知识点。

















 9325
9325

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










