【自动驾驶】摄像头单目测距原理及实现

原文链接：摄像头单目测距原理及实现
可以观看这个视频，了解针孔相机和透镜。

---

求地面上的点距离相机的深度距离，方法如下：

对于相机坐标系变换到像素坐标系，有下面公式：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}f/dx& 0& u_0\\ 0& f/dy& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c/Z_C\\ Y_c/Z_c\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c/Z_C\\ Y_c/Z_c\\ 1\end{array}\right]$$
其中，$(X_c,Y_c,Z_c)$是相机坐标系下的一点，$(u,v,1)$是像素坐标系下的一点。
当我们在实际情况中，已知物体在水平地面，并且相机高度已知的情况，那么可以根据上面的等式第二行，得到：
$v=f_y\ast Y_c/Z_c+v_0$，移项化简得到：
$$Z_c=\frac{f_y\ast Y_c}{v-v_0}$$
这个等式右边：

• $f_y$ 是相机内参，通过标定获得；
• $Y_C$ 是地面上的点在相机坐标系下的Y坐标，就是相机距离地面的高度，通过测量获得；
• $v$ 是地面上的点在像素坐标系下的点y坐标，从(图片)像素坐标系下获取，已知；
• $v_0$ 是相机内参，通过标定获得；

因此，地面上的点距离相机的距离$Z_C$就得到了。

---

摄像头单目测距原理及实现

一．测距原理

空间的深度或距离等数据的摄像头。

人的眼睛长在头部的前方，两只眼的视野范围重叠，两眼同时看某一物体时，产生的视觉称为双眼视觉。

双眼视觉的优点是可以弥补单眼视野中的盲区缺损，扩大视野，并产生立体视觉。

也就是说，假如只有一只眼睛，失去立体视觉后，人判断距离的能力将会下降。

这也就是单目失明的人不能考取驾照的原因。

单纯的单目视觉测距，必须已知一个确定的长度。

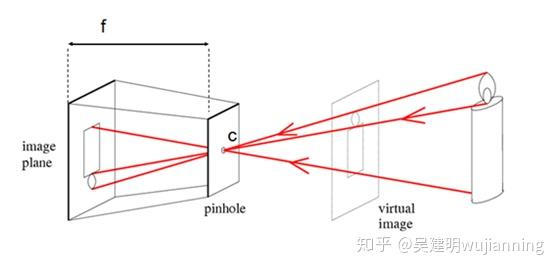
f为摄像头的焦距，c为镜头光心。物体发出的光经过相机的光心，然后成像于图像传感器或者也可以说是像平面上，如果设物体所在平面与相机平面的距离为d，物体实际高度为H，在传感器上的高度为h，H一定要是已知的，我们才能求得距离d。

下面的相机焦距f并不是透镜的焦距，而是焦距+z0,这个我们必须要清楚。因为成像是在像平面，并不是成像在焦平面，焦平面的距离才是f，但是我们下面的模型不需要知道实际的f，所以就使用了像平面的距离焦距f+z0作为相机焦距f。

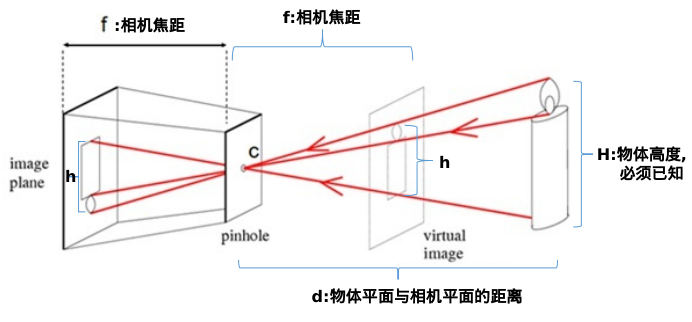
由相似三角形，可以得到:
$$\frac{h}{H}=\frac{f}{d}$$

第一步，求相机焦距：

对于蜡烛，我们可以：

• 1.测量蜡烛的高度 $H$，作为先验知识；
• 2.测量蜡烛到相机光心的距离 $d$;
• 3.通过相机拍摄的这一帧蜡烛图像，可以得到蜡烛在图像中的高度所占像素个数 $h$；

知道了$H,h,d$这三个量，就可以求出相机的焦距$f$，即：
$$f=\frac{h\ast d}{H}$$
需要注意，相机的焦距是个固定值，只要使用该方法求出焦距后，以后就不用再求了。但是，可能需要多次测量求平均值。

第二步，求物体距离相机的实际距离：

得到了相机焦距$f$，对于放在其他位置的任意物体，就可以根据：

• 1.该物体的先验值高度 $H$；
• 2.统计出该物体在该帧图像中的高度所占像素个数 $h$；
• 3.前面求出来的相机焦距固定值 $f$；

得到物体距离相机的实际距离$d$：

$$d=\frac{H\ast f}{h}$$

---

同理，你也可以通过测量蜡烛的宽度来求相机的焦距$f$。
假设我们有一个宽度为 W 的目标或者物体。然后我们将这个目标放在距离我们的相机为d 的位置。我们用相机对物体进行拍照并且测量物体的像素宽度w 。这样我们就得出了相机焦距的公式：$$f=\frac{w\ast d}{W}$$
例如，假设现在我们有一张A4纸（8.27in x 11.69in), in代表英寸，1in = 25.4mm。
纸张宽度W=11.69in，相机距离纸张的距离d = 32in。
此时拍下的照片中A4纸的像素宽度为w=192px（我的相机实际测量得到的值）。
此时我们可以算出焦距$$f=（192\ast 30)/11.69$$
当我们将摄像头远离或者靠近A4纸时，就可以用相似三角形得到相机距离物体的距离。
此时的距离： $$d^{\prime }=\frac{W^{\prime }\ast f}{w^{\prime }}$$

注意：这里测量的距离是相机到物体的垂直距离，产生夹角，测量的结果就不准确了。为什么？下图说明结果并不会不准确啊？

二．测距步骤：

• 1.使用摄像机采集道路前方的图像；
• 2.在道路区域对物体进行检测，通过矩形框将物体形状框出来。
• 3.结合矩形框信息，找到该矩形框底边的两个像平面坐标，分别记为（u1，v1）和（u2，v2）;
• 4.使用几何关系推导法，由像平面坐标点（u1, v1）、（u2, v2）推导出道路平面坐标（x1,y1）、（x2, y2）；（投影到地面上，z轴为0）
• 5.通过欧氏距离公式计算出d。

三．难点整理：

• 1.图像畸变矫正模型的理解;

  （标定参数，内参矩阵，畸变矩阵，外参矩阵（平移、旋转向量矩阵））

• 2.像素坐标与世界坐标公式的推导及验证；
• 3.测距方法，对于检测物体在摄像头前方、左侧、右侧的判别思路；(为什么？)
• 4.弄清反畸变；对于畸变矫正后的图像中的检测框中的点进行反畸变处理。

四．相机镜头畸变矫正–>得到相机的内外参数、畸变参数矩阵

1. 外参数矩阵。世界坐标经过旋转和平移，然后落到另一个现实世界点(摄像机坐标)上。

2. 内参数矩阵。告诉你上述那个点在1的基础上，是如何继续经过摄像机的镜头、并通过针孔成像和电子转化而成为像素点的。

3. 畸变矩阵。告诉你为什么上面那个像素点并没有落在理论计算该落在的位置上，还产生了一定的偏移和变形.

---

五．实现代码

#!/usr/bin/python3

# -- coding: utf-8 --

# Date: 18-10-29

import numpy as np # 导入numpy库

import cv2 # 导入Opencv库

KNOWN_DISTANCE = 32 # 这个距离自己实际测量一下

KNOWN_WIDTH = 11.69 # A4纸的宽度

KNOWN_HEIGHT = 8.27

IMAGE_PATHS = [“Picture1.jpg”, “Picture2.jpg”, “Picture3.jpg”] # 将用到的图片放到了一个列表中

# 定义目标函数

def find_marker(image):

gray_img = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY) # 将彩色图转化为灰度图

gray_img = cv2.GaussianBlur(gray_img, (5, 5), 0) # 高斯平滑去噪

edged_img = cv2.Canny(gray_img, 35, 125) # Canny算子阈值化

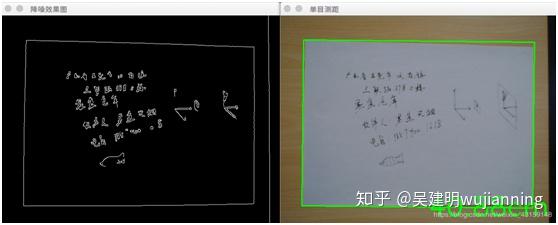
cv2.imshow(“降噪效果图”, edged_img) # 显示降噪后的图片

# 获取纸张的轮廓数据

img, countours, hierarchy = cv2.findContours(edged_img.copy(), cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)

# print(len(countours))

c = max(countours, key=cv2.contourArea) # 获取最大面积对应的点集

rect = cv2.minAreaRect© # 最小外接矩形

return rect

# 定义距离函数

def distance_to_camera(knownWidth, focalLength, perWidth):

return (knownWidth * focalLength) / perWidth

# 计算摄像头的焦距（内参）

def calculate_focalDistance(img_path):

first_image = cv2.imread(img_path) # 这里根据准备的第一张图片，计算焦距

# cv2.imshow(‘first image’, first_image)

marker = find_marker(first_image) # 获取矩形的中心点坐标，长度，宽度和旋转角度

focalLength = (marker[1][0] * KNOWN_DISTANCE) / KNOWN_WIDTH # 获取摄像头的焦距

# print(marker[1][0])

print('焦距(focalLength) = ', focalLength) # 打印焦距的值

return focalLength

# 计算摄像头到物体的距离

def calculate_Distance(image_path, focalLength_value):

image = cv2.imread(image_path)

# cv2.imshow(“原图”, image)

marker = find_marker(image) # 获取矩形的中心点坐标，长度，宽度和旋转角度， marke[1][0]代表宽度

distance_inches = distance_to_camera(KNOWN_WIDTH, focalLength_value, marker[1][0])

box = cv2.boxPoints(marker)

# print("Box = ", box)

box = np.int0(box)

print("Box = ", box)

cv2.drawContours(image, [box], -1, (0, 255, 0), 2) # 绘制物体轮廓

cv2.putText(image, “%.2fcm” % (distance_inches * 2.54), (image.shape[1] - 300, image.shape[0] - 20),

cv2.FONT_HERSHEY_SIMPLEX, 2.0, (0, 255, 0), 3)

cv2.imshow(“单目测距”, image)

if name == “main”:

img_path = “Picture1.jpg”

focalLength = calculate_focalDistance(img_path)

for image_path in IMAGE_PATHS:

calculate_Distance(image_path, focalLength)

cv2.waitKey(0)

cv2.destroyAllWindows()