【概述】
斐波那契数列(Fibonacci sequence),又称黄金分割数列,其指的是这样一个数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368....这个数列从第 3 项开始,每一项都等于前两项之和。
斐波那契数列除应用递推、递归定义解题外,还可用于改进二分查找——斐波那契数列查找。
关于斐波那契查找:点击这里
【特性】
- 奇数项求和:
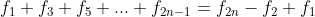
- 偶数项求和:
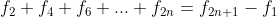
- 平方求和:
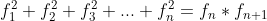
- 二倍项关系:
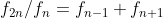
- 平方项与隔项:
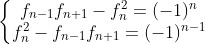
- 公约数:
![GCD(f[m],f[n])=f[GCD(m,n)]](https://i-blog.csdnimg.cn/blog_migrate/283d6018385b0be560115588232a5978.gif)
【公式】
1.通项公式

2.递推公式
根据定义可知:F0=0,F1=1,F2=F1+F0=1,F3=F2+F1=2,F4=F3+F2=3,F5=F4+F3=5,……
int Fibonacci(int n)
{
if (n<0)
return -1;
int n1=1,n2=2,n3=3;
for (int i=3;i<=n;++i)
{
n3=n1+n2;
n1=n2;
n2=n3;
}
return n3;
} 3.递归公式
如果设 F(n)为该数列的第n项,那么斐波那契数列可以写成如下形式: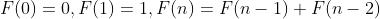
int fibonacci(int n)
{
if (n == 1 || n == 2)// 递归终止条件
return 1;// 简单情景
return fibonacci(n-1)+fibonacci(n-2); // 相同重复逻辑,缩小问题的规模
}

























 947
947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








