基于麻雀算法优化的相关向量机RVM回归预测算法

基于麻雀算法优化的相关向量机RVM回归预测算法

摘要：本文主要介绍相关向量机RVM的基本原理，以及在预测问题中的应用。

1.RVM原理

RVM算法是一种基于贝叶斯框架的机器学习模型 ，通过最大化边际似然得到相关向量和权重。

设 { x } u = 1 N \{x\}_{u=1}^N {x}u=1N​​和 { t } u = 1 N \{t\}_{u=1}^N {t}u=1N​​分别是输入向量和输出向量，目标$t$​可采用如式(1)所示的回归模型获得:
$$t=y(x)+{\xi }_n\text{\hspace{1em}(1)}$$
式中: ${\xi }_n$为零均值、方差 ${\sigma }^2$的噪声，$y(x)$ 定义为:
$$y(x)=\sum _{u=1}^N{w}_{u}K(x,x_u)+w_0\text{\hspace{1em}(2)}$$
式中: $K(x,x_u)$ 是核函数，$w_u$ 是权重向量，$w_0$是偏差。设$t$​是独立的，其概率定义为:
$$p(t|w,{\sigma }^2)=(2\pi {\sigma }^2{)}^{-N/2}exp(-\frac{||t-w\phi |{|}^2}{2{\sigma }^2})\text{\hspace{1em}(3)}$$
式中：$t=(t_1,t_2,...,t_N{)}^T,w=(w_0,w_1,...,w_n{)}^T$,$\phi$是$N(N+1)$​的矩阵。

式(3)中的 $w$ 和 $\sigma$最大似然估计会导致过拟合，为约束参数，定义一个零均值高斯先验概率分布:
$$p(w|\alpha )=\prod _{u=0}^{N}N(w_u|0,{\alpha }_u^{-1})\text{\hspace{1em}(4)}$$
式中: $\alpha$ 是 $N+1$ 维的超参数向量。

依据贝叶斯公式，未知参数的后验概率为:
$$p(w,\alpha ,{\sigma }^2|t)=p(w|\alpha ,{\sigma }^2,t)p(\alpha ,{\sigma }^2|t)\text{\hspace{1em}(5)}$$
后验分布的权重被描述为:
$$p(w|t,\alpha ,{\sigma }^2)=(2\pi {)}^{-(N+1)/2}|\Sigma {|}^{-1/N}exp(-\frac{1}{2}(w-u{)}^T{\Sigma }^{-1}(w-u))\text{\hspace{1em}(6)}$$
式中:后验均值$u={\sigma }^{-2}\Sigma {\phi }^{T}t$,协方差$\Sigma =({\sigma }^{-2}{\phi }^T\phi +A{)}^{-1}$,$A=diag({\alpha }_0,{\alpha }_1,...,{\alpha }_N)$​。

为了实现统一的超参数，​做出如下定义:
$$p(t|\alpha ,{\sigma }^2)=\int p(t|w,{\sigma }^2)p(w,\alpha )dw=(2\pi {)}^{-N/2}|{\sigma }^{2}I+\phi A^{-1}{\phi }^T|exp(-\frac{1}{2}{t}^T({\sigma }^{2}I+\phi A^{-1}{\phi }^T{)}^{-1}t)\text{\hspace{1em}(7)}$$
高斯径向基函数具有较强的非线性处理能力，被用作核函数，其定义如下:
$$K(x,x_u)=exp(-\frac{(x-x_u{)}^2}{2{\gamma }^2})\text{\hspace{1em}(7)}$$
式中: $\gamma$ 为宽度因子，对模型的精度有极大的影响，需要预先设定。

2.基于麻雀算法优化的相关向量机RVM

麻雀算法的基本原理请参考我的博客：https://blog.csdn.net/u011835903/article/details/108830958

本文利用麻雀算法优化RVM的宽度因子和超参数。适应度函数设计为训练集预测结果与真实值的MSE。MSE越低表明算法的预测性能越好。
$$fitness=MSE(Predict-truth)\text{\hspace{1em}(8)}$$

3.算法实验与结果

本文算法数据数量一共为250组数据。其中前200组数据用训练，后50组数据用作测试数据。数据的输入维度为2维，输出维度为1维。

数据类别	数据量
训练数据	200
测试数据	50

设置麻雀算法的参数如下：

%% 麻雀参数设置
pop=20; %种群数量
Max_iteration=20; %  设定最大迭代次数
dim = 3;% 维度为2，即优化两个超参数，已经核宽度
lb = [0.1,0.1,0.1];%下边界
ub = [1,1,10];%上边界

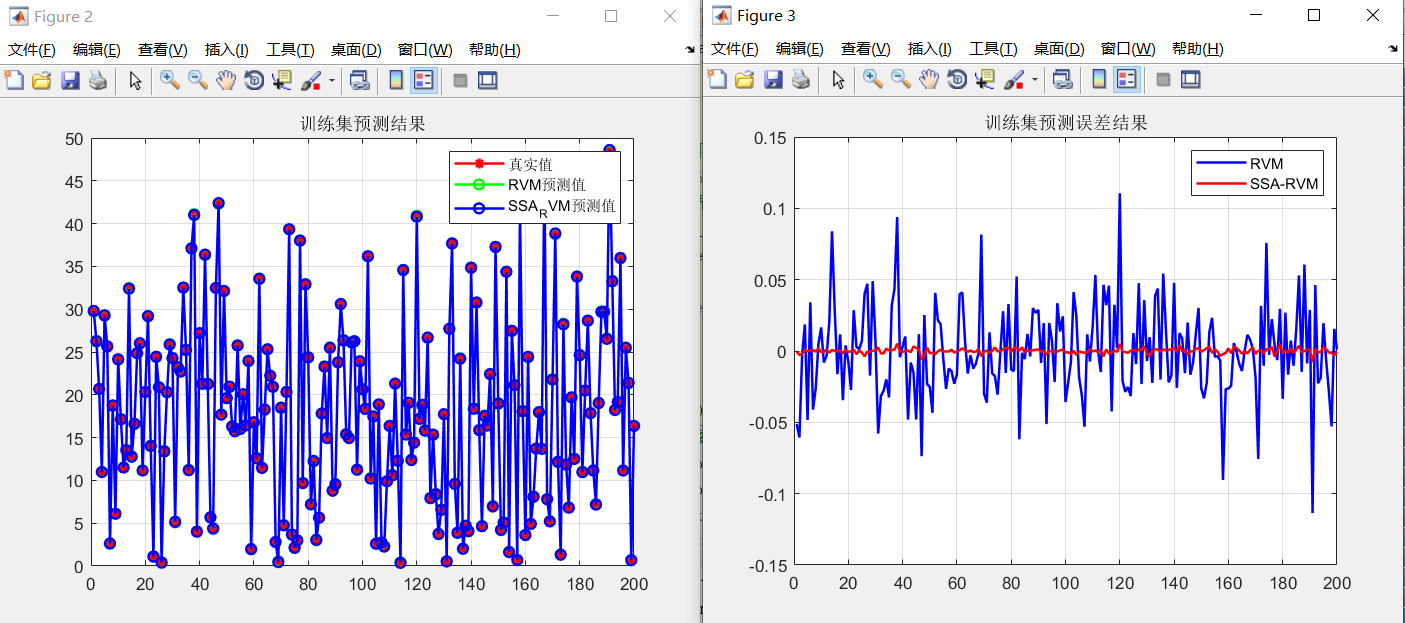
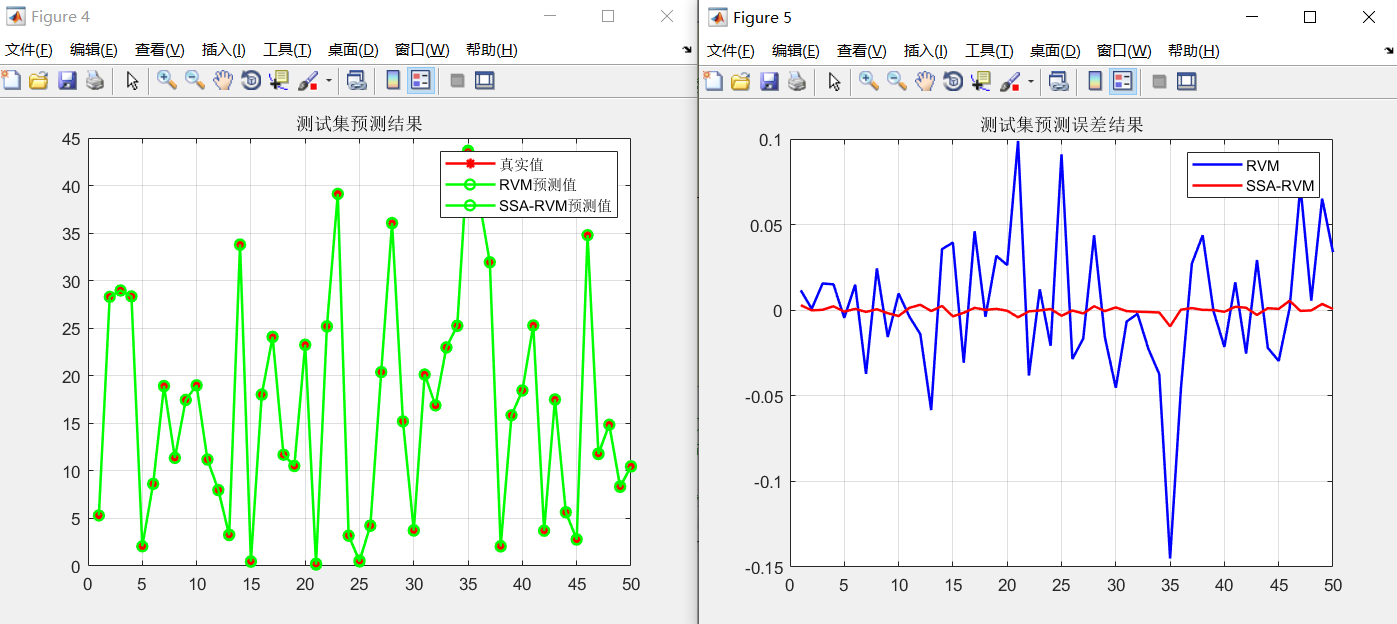
RVM训练集MSE：0.0010558
RVM测试集MSE：0.0016356
SSA-RVM训练集MSE：3.1329e-06
SSA-RVM测试集MSE：5.2491e-06

从结果曲线，和训练集MSE以及测试集MSE来看，SSA-RVM相比基础RVM在回归预测问题上表现了较好的结果。

3.参考文献：

[1] TIPPPING M E． Sparse Bayesian learning and the relevance vector machine［J］． The journal of machine learning research，2001，1: 211-244．

4.MATLAB代码