理解復數的乘法
把復數看作是旋轉是我最喜歡的一個“茅塞頓開”的例子。

i,-1的平方根,是一個存在於不同維度的數!一旦把它想通了,我們就可以把復數的旋轉與乘法聯繫起來。

啊哈,這個確實讓我很驚訝:角度增加但是不需要用到Sin或Cos!但是我對它是如何作用的有一個直觀的理解。現在讓我們彌補一下這個缺憾!
EX.1 最乏味的解釋:怎麼會這樣?
這裏有一個經常被提到的用來解釋為什麼復數相乘就是角度相加的闡述。
首先,把復數寫成極座標系下的形式(弧度或角度):

接下來,進行乘法運算,實部與虛部分別進行運算:

最後,註意到它們正好符合三角函數的和差化積公式:

這樣你就得到了想要的結果!那是什麼呢?憑你的直覺你是想不到其中會涉及到Sin與Cos的?太糟糕了,隻是數學驗證確實復合!
……
還卡在這裏?很好。問題就出在我們沒有找到其中的奇妙之處:這就像是說兩首詩很相似,因為我們研究了其中的字詞排列。很精確但是不能讓人滿意!
我跟大家一樣十分喜歡Sin,但是其中的細節需要等到我們看到了其中的關係後才能明了。
EX.2 有趣的解釋:為什麼會這樣!
這次我們的目標是什麼?哦,是的——要理解為什麼復數相乘就等效於角度相加。
首先,讓我們看看乘法都做了些什麼:

- 普通乘法(“乘以2”)將一個數按比例縮放(讓它變大或變小)
- 虛數乘法(“乘以i”)將你旋轉90度
如果我們在一個復數中把這些結合起來呢?比如說乘以(2+i)表示“把數翻倍——呃,然後再加上一個垂直旋轉”。
一個簡單的例子:
4·(3+i)=4·3+4·i=12+4i
這就是說,原來的數(4),放大三倍(4×3),然後再進行旋轉(+4i)。再一次的,如果我們隻需要旋轉,我們隻需乘以“i”。如果我們需要縮放隻需要乘上一個普通的數字。一個復數(a+bi)可以同時實現以上兩種效果。
EX.3 形象化表示復數乘法
這很簡單——對於一個實數(4)乘以一個復數(3+i)來說。那麼如果是兩個復數相乘呢(“角度”),比如說:
(3+4i)·(2+3i)

我們現在正在討論。我看到了“原來的復數縮放後的版本(2)與旋轉後的版本(3i)相加”。終點就表示一個新的復數。
但是……我更喜歡另一個解釋!以下就是詳細說明:

不再是根據角度把乘法分開進行運算,我們分析這一薄片(FOIL,正好是第一部分First,外部Outside,內部Inside,最後一部分Last的首字母縮寫)的每一部分。沿著路徑我們把每一部分分別相加,終點與起點不变!
EX.4 可是角度怎麼辦呢?
啊,對,還有角度。好像我們是把角度加起來了,但是我們能肯定嗎?
帶領幾何大軍來救援吧!哦,自從我初中畢業後我是多麼想念你啊。最終的結果(藍色的虛線)跟把角度單獨相加的結果是否一致呢?
在之前的解釋中,我們從(3+4i)開始,加上(2+3i)後得到最後的角度。
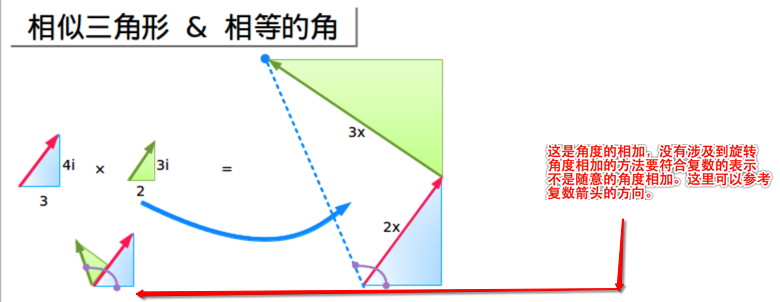
經過乘法運算以後,我們從一個縮放後的三角形(2倍大)開始,然後加上了另一個縮放後的三角形(乘以3i)。即便如此它也是變大了,相似三角形對應的內角角度相同——它們隻是大小不同而已(先不必關心面積的變化,好吧?)。
我們縮放了原來的三角形(但是沒有改變角度),然後“加上了”另一個縮放後的三角形(同樣沒有改變角度),所以結果是相同的!我喜歡看到這些結果匯 總在一起——我們進行縮放,旋轉,然後爆發——我們得到了最後的角度。這個與“虛數”無關——我們可以不通過幾何而對角度進行組合!
EX.5 縮放時可能會產生的副作用
註意我們是如何把原來的三角形進行縮放並相加在一起的。跟剛開始時的藍色三角形相比我們大小發生了怎樣的變化?
好吧,讓我們假定原來的長度為“x”,不管它是多少,我們最後總能得到一個新的三角形,它的尺寸變為2x+3x(一般說來就是a+bi)。通過畢達哥拉斯定理(我喜歡這位先生)我可以知道“實在”的距離就是
【管注解:根号( (ax)² + (bx)²) = 根号( x² (a² + b²)) = x 根号(a² + b²) ,这里 a+bi,a 和 b 表示缩放,x表示原来的长度,如下图】
這就是說,原來的距離(x)通過新的三角形被縮放了(大小為a+bi)。
如果新的三角形的大小是1(a^2+b^2=1),那麼距離就不會改變!
EX.6 一些思考
我並不憎恨嚴謹的證明——我討厭明明它們起不到作用時還要假裝它們很有用。證明有兩個目的:
- 說明結果是正確的。這是數學家展示結果是必須要做的——但是數學課上學生很少對其真實性表示質疑。
- 告訴大家結果為什麼是真的。
通過類比與示例可以傳達一種真實的並且讓人滿意的洞見——而不是去閱讀精簡過的短小證明(特別是涉及到三角函數公式的)
George Pólya說得好:“當你自己認可了一個理論後再去證明它”
希望你能享受到美好的數學。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








