深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

前言

（标题不能再中二了）本文仅对一些常见的优化方法进行直观介绍和简单的比较，各种优化方法的详细内容及公式只好去认真啃论文了，在此我就不赘述了。

SGD

此处的SGD指mini-batch gradient descent，关于batch gradient descent, stochastic gradient descent, 以及 mini-batch gradient descent的具体区别就不细说了。现在的SGD一般都指mini-batch gradient descent。

SGD就是每一次迭代计算mini-batch的梯度，然后对参数进行更新，是最常见的优化方法了。即：

$$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1})}$$ $$\Delta{\theta_t}=-\eta*g_t$$
其中， $\eta$是学习率， $g_t$是梯度

SGD完全依赖于当前batch的梯度，所以$\eta$可理解为允许当前batch的梯度多大程度影响参数更新

缺点：（正因为有这些缺点才让这么多大神发展出了后续的各种算法）

• 选择合适的learning rate比较困难
• 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征，有时我们可能想更新快一些对于不经常出现的特征，对于常出现的特征更新慢一些，这时候SGD就不太能满足要求了
• SGD容易收敛到局部最优，在某些情况下可能被困在鞍点【但是在合适的初始化和学习率设置下，鞍点的影响其实没这么大】

Momentum

momentum是模拟物理里动量的概念，积累之前的动量来替代真正的梯度。公式如下：

$$m_t=\mu*m_{t-1}+g_t$$
$$\Delta{\theta_t}=-\eta*m_t$$
其中， $\mu$是动量因子

特点：

• 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的$\mu$能够进行很好的加速
• 下降中后期时，在局部最小值来回震荡的时候，$gradient\to0$，$\mu$使得更新幅度增大，跳出陷阱
• 在梯度改变方向的时候，$\mu$能够减少更新

总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛

Nesterov

nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度。
将上一节中的公式展开可得：

$$\Delta{\theta_t}=-\eta*\mu*m_{t-1}-\eta*g_t$$
可以看出， $m_{t-1}$并没有直接改变当前梯度 $g_t$，所以Nesterov的改进就是让之前的动量直接影响当前的动量。即：
$$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1}-\eta*\mu*m_{t-1})}$$
$$m_t=\mu*m_{t-1}+g_t$$
$$\Delta{\theta_t}=-\eta*m_t$$
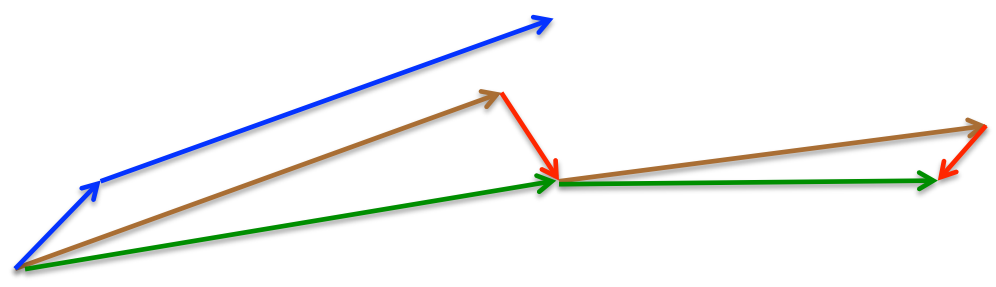
所以，加上nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。如下图：

momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

其实，momentum项和nesterov项都是为了使梯度更新更加灵活，对不同情况有针对性。但是，人工设置一些学习率总还是有些生硬，接下来介绍几种自适应学习率的方法

Adagrad