采样之拒绝采样

注：本文中所有公式和思路来自于邹博先生的《机器学习升级版》，我只是为了加深记忆和理解写的本文。

第一次接触到采样这个词的时候我感觉别扭，因为觉得不是有现成的样本数据么，直接处理后喂给模型不就行了么干嘛要多此一举呢？

其实我们可以这样来理解采样：

采样时前提是我们已经确定一个系统(概率分布)，但是不知道满足该分布背后的参数，然后我们根据这个概率分布从所有的样本中采样出n个样本，那么这n个样本必然也是满足这个概率分布，我们通过这些样本，将参数求出来。

我们都比较熟悉这样的方式：给定样本数据，然后通过优化极值来求得参数(SVM、logistic等)，这是频率学派的做法，在贝叶斯学派中，会用到采样的方式求得参数，地位上采样和优化是对等的。

这次先介绍一种采样方法--拒绝采样

从字面上便知，拒绝采样：带拒绝的采样

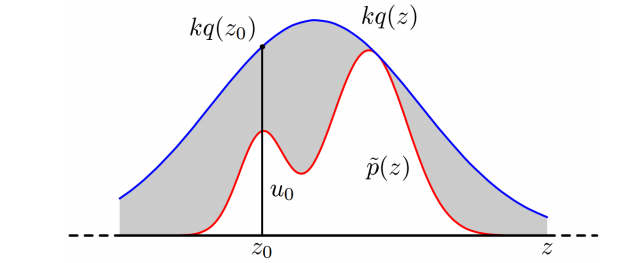
解释：假定现在有一个分布p(z)，但很遗憾，这个分布很复杂，我们不太容易直接按照p(z)分布采样，此时我们总是可以找到一个容易采样的分布q(z)(例：高斯分布)，我们将q(z)乘以一个系数k总可以拉伸这个分布，将原分布p(z)完全覆盖掉，如下图蓝色的线。

这样的话我们就可以在这个q(z)中做均匀采样，如果满足p(z)则接受该样本，不满足就拒绝掉。

再举一个小例子，假如现在要想在单位圆内做均匀采样：

方法一：我们就可以在单位圆外边画一个外切正方形，做拒绝采样，从而得到圆内的均匀样本。

方法二：

我们假设有两个从0到1的随机数，a，b。那么，我们另： r = a 
      theta = b * 2 * Pi 
上述随机点显然可以布满整个圆，但是并不是均匀分布的，简单略。
实际上，通过inverse sampling method，我们可以计算出正确的生成算法，即 
      r = sqrt( a ) 
      theta = b * 2 * Pi 
上述算法就是满足要求的了，即可以在圆的内部均匀分布了

拒绝采样的过程和思路比较简单，但是也有个显然易见的问题，会有一部分样本被丢弃掉，效率上也会差一些。后边会介绍更多的采样方法。

单位圆内均匀采样摘自就不告诉你1111的文章