4.1散点数据插值 194
4.1.1径向基函数 196
4.1.2过拟合和欠拟合 199
4.1.3稳健的数据拟合 202
4.2变分法和正则化 204
4.2.1离散能量最小化 206
4.2.2总变异 210
4.2.3双侧求解器 210
4.2.4应用:交互式着色 211
4.3马尔可夫随机场 212
4.3.1条件随机场 222
4.3.2应用:交互式分割 227
4.4其他阅读材料 230
4.5练习 232

图4.1数据插值和全局优化示例:(a)散点数据插值(曲线拟合)(Bishop2006)©2006斯普林格;(b)一阶正则化的图形模型解释;(c)使用优化进行着色(Levin,Lischinski,和Weiss 2004)©2004 ACM;(d)多图像拼接被表述为无序标签MRF(Agarwala,Dontcheva等2004)©2004 ACM。
在上一章中,我们介绍了大量图像处理操作符,这些操作符以一张或多张图像作为输入,并生成这些图像的某种过滤或转换版本。然而,在许多情况下,我们得到的是不完整的数据作为输入,例如稀疏位置的深度信息,或者用户涂鸦建议如何对图像进行着色或分割(图4.1c-d)。
从不完整或质量参差的数据中插值出完整的图像(或更广泛地说,是一个函数或场)的问题通常被称为散点数据插值。本章开篇将回顾这一领域的技术,因为除了在计算机视觉中广泛应用外,这些技术也是大多数机器学习算法的基础,我们将在下一章详细探讨。
我们没有进行详尽的调查,而是在第4.1节介绍了一些易于使用的技巧,如三角测量、样条插值和径向基函数。尽管这些技术被广泛使用,但它们难以调整以提供受控的连续性,即无法生成我们在估计深度图、标签图甚至彩色图像时所期望的那种分段连续的重建。
为此,我们在第4.2节介绍了变分方法,这些方法将插值问题表述为在精确或近似数据约束下恢复分段光滑函数。由于平滑度是通过作为函数范数的惩罚来控制的,这类技术通常被称为正则化或基于能量的方法。为了找到这些问题的最小能量解,我们对其进行离散化(通常是在像素网格上),从而得到一个离散的能量函数,然后可以使用稀疏线性系统或相关的迭代技术进行最小化。
在本章的最后一部分,第4.3节中,我们展示了基于能量的公式如何与作为马尔可夫随机场形式化的贝叶斯推断技术相关联,后者是通用概率图模型的一个特例。在这些公式中,数据约束可以解释为噪声和/或不完整的测量,而分段平滑约束则作为先验假设或解决方案空间的模型。这类公式通常也被称为生成模型,因为原则上可以从先验分布中生成随机样本,以检验它们是否符合我们的预期。由于先验模型可以比简单的平滑约束更复杂,且解决方案空间可能有多个局部最小值,因此需要使用更为复杂的优化技术。
散点数据插值的目标是产生一个(通常连续且平滑的)函数f(x),该函数通过一组位于位置xk的数据点dk,使得
f (xk) = dk . (4.1)
散点数据逼近的相关问题只需要函数在数据点附近通过(Amidror2002;Wendland2004;Anjyo、Lewis和Pighin2014)。这通常使用惩罚函数来表述,例如
- dk Ⅱ2 ; (4.2)
在上述公式中,平方范数有时会被不同的范数或稳健函数所替代(第4.1.3节)。在统计学和机器学习中,给定有限数量样本预测输出函数的问题称为回归(第5.1节)。向量x被称为输入,而输出y则被称为目标。图4.1a展示了一维散点数据插值的一个例子,而图4.2和4.8则展示了几个二维的例子。
乍一看,散点数据插值似乎与我们在第3.5.1节中研究的图像插值密切相关。然而,与图像不同的是,图像中的数据点是规则网格化的,而散点数据插值中的数据点在整个域内分布不规则,如图4.2所示。这需要我们对所使用的插值方法进行一些调整。
如果域x是二维的,如图像所示,一种简单的方法是使用数据点xk作为三角形顶点来三角化域x。所得的三角网络如图4.2a所示,称为不规则三角网(TIN),这是早期用于从散射场测量数据生成高程图的技术之一。
图4.2a中的三角剖分是使用Delaunay三角剖分生成的。Delaunay三角剖分因其计算特性而被广泛采用,例如避免长条形三角形。高效的计算此类三角剖分的算法现已有现成的解决方案,并在计算几何教科书中有所介绍(Preparata和Shamos 1985;de Berg,Cheong等人2008)。利用外接球的性质,即所有选定的单纯形(如三角形、四面体等)在其外接球内没有其他顶点的要求,Delaunay三角剖分可以扩展到更高维度的空间。

图4.2一些简单的散点数据插值和逼近算法:(a)
一种定义在一组数据点位置上的Delaunay三角化;(b)用于拉推算法的数据结构和中间结果(Gortler,Grzeszczuk (et al.1996)©1996 ACM。
一旦三角剖分确定,就可以轻松地在每个三角形上定义一个分段线性插值函数,从而得到一个C0连续但通常不是C1连续的插值函数。每个三角形内的函数公式通常是使用重心坐标推导出来的,这些坐标在顶点处取最大值,并且总和为一(Farin2002;Amidror2002)。
如果需要更平滑的表面作为插值函数,我们可以用高阶样条函数替换每个三角形上的分段线性函数,就像我们在图像插值中所做的那样(第3.5.1节)。然而,由于这些样条现在是在不规则三角剖分上定义的,因此必须使用更复杂的技术(Farin2002;Amidror2002)。其他基于计算机图形学中的几何建模技术的插值器还包括细分曲面(Peters和Reif2008)。
三角化数据点的替代方法是使用如图4.2b所示的规则n维网格。定义在该域上的样条通常称为张量乘积样条,并且已用于插值散射数据(Lee、Wolberg和Shin,1997)。
一种更快但不那么精确的方法称为拉推算法,最初是为在Lumigraph中插值缺失的4D光场样本而开发的(Gortler、Grzeszczuk等人,1996)。该算法分为三个阶段,如图4.2b所示。
首先,不规则数据样本被散布到最近的网格顶点上(即,分布在这些顶点上),使用我们在第3.6.1节讨论的参数图像变换方法。散布操作会在附近的顶点累积值和权重。在第二阶段,通过结合高分辨率网格的系数值,在一系列低分辨率网格中计算值和权重。在较低的
分辨率网格中,间隙(权重较低的区域)变得越来越小。在第三阶段,即推移阶段,每个较低分辨率网格的信息与下一个较高分辨率网格的信息结合,填补这些间隙,同时不会过度模糊已经计算出的高分辨率信息。这三个阶段的详细内容可参见(Gortler,Grzeszczuk等1996)。
拉推算法非常快,因为它本质上是线性的输入数据点和精细网格样本的数量。
虽然我刚才描述的基于网格的表示可以提供高质量的插值,但它们通常仅限于低维域,因为网格的大小会随着域的维度呈组合增长。在高维情况下,通常使用无网格方法,将所需的插值定义为基函数的加权和,类似于图像插值中使用的公式(3.64)。在机器学习中,这些方法常被称为核函数或核回归(Bishop2006,第6章;Murphy2012,第14章;Scho...lkopf和Smola2001)。
更详细地说,插值函数f是每个输入数据点中心的基础函数的加权和(或叠加)
(4.3)
其中,xk是散射数据点的位置,φs是径向基函数(或核函数),wk是与每个核相关的局部权重。基函数φ()称为径向的,因为它们应用于数据样本xk和评估点x之间的径向距离。φ的选择决定了插值函数的平滑特性,而权重wk的选择则决定了函数对输入的逼近程度。
一些常用的基函数(Anjyo、Lewis和Pighin2014)包括

在这些方程中,r是径向距离,c是一个尺度参数,它控制基函数的大小(径向衰减),因此它的平滑度(更紧凑的基函数会导致
“峰值”解)。薄板样条方程适用于二维(一般n维样条称为多谐样条,见(Anjyo,Lewis,和Pighin2014)),是(4.19)中推导出的二阶变分样条的解析解。
如果我们要使函数精确地插值数据值,我们求解线性方程组(4.1),即:
dk , (4.8)
为了获得所需的权重向量wk。请注意,当基函数重叠较大(c值较大)时,这些方程可能会非常病态,即数据值或位置的微小变化可能导致插值函数发生显著变化。还需注意,这类方程组的解通常为O(m^3),其中m是数据点的数量(除非我们使用有限范围的基函数以获得稀疏方程组)。
一种更为谨慎的方法是解决正则化数据近似问题,该问题涉及最小化数据约束能量(4.2)以及形式如下的权重惩罚(正则化器)
wk Ⅱp , (4.9)
然后最小化正则化最小二乘问题
当p=2(二次权重惩罚)时,得到的能量是一个纯最小二乘问题,并且可以使用正规方程(附录A.2)来解决,其中λ值沿着对角线添加以稳定方程组。
在统计学和机器学习中,二次(正则化最小二乘)问题被称为岭回归。在神经网络中,对权重添加二次惩罚称为权重衰减,因为它鼓励权重向零衰减(第5.3.3节)。当p = 1时,该技术被称为套索回归(最小绝对收缩和选择算子),因为对于足够大的λ值,许多权重wk会被驱动到零(Tibshirani 1996;Bishop 2006;Murphy 2012;Deisenroth,Faisal,和Ong 2020)。这导致在插值中使用了一组稀疏的基础函数,可以大大加快计算新f (x)值的速度。我们将在支持向量机部分(第5.1.4节)进一步讨论稀疏核技术。
求解一组方程以确定权重wk的替代方法是简单地将它们设置为输入数据值dk。然而,这无法插值数据,而是
在高密度区域产生更高的值。这在我们试图从一组样本中估计概率密度函数时非常有用。在这种情况下,通过将样本加权基函数之和归一化为单位积分得到的结果密度函数被称为帕森窗口或核方法的概率密度估计(Duda、Hart和Stork 2001,第4.3节;Bishop 2006,第2.5.1节)。这些概率密度可用于(空间上)聚类颜色值以进行图像分割,即所谓的均值漂移方法(Comaniciu和Meer 2002)(第7.5.2节)。
如果,我们不只估计密度,而是希望实际插值一组数据值dk,我们可以使用一种相关技术,称为核回归或Nadaraya-Watson模型,在这种模型中,我们将数据加权的基函数之和除以所有基函数之和,
(4.12)
注意,从概念上讲,此操作与我们在第3.6.1节中讨论的正向渲染的喷溅法类似,不同之处在于,这里的基可以比图形中使用的最近邻双线性基宽得多(Takeda,Farsiu和Milanfar2007)。
核回归等同于创建一组新的空间变化的归一化移位基函数
(4.13)
它们构成单位分量,即在每个位置的总和为1(Anjyo、Lewis和Pighin 2014)。现在,所得插值可以更简洁地表示为
(4.14)
在大多数情况下,预先计算和存储Kφ函数
比存储更昂贵
评估(4.12)。
虽然在计算机视觉中没有被广泛使用,但Takeda、Farsiu和Milanfar(2007)已经将核回归技术应用于许多低级图像处理操作,包括最先进的手持多帧超分辨率(Wronski、Garcia-Dorado等人,2019)。
最后值得一提的一种散点插值技术是移动最小二乘法,该方法使用附近点的加权子集来计算局部平滑表面。这类技术在三维计算机图形学中广泛应用,尤其是在基于点的表面建模方面,详见第13.4节及(Alexa,Behr等,2003;Pauly,Keiser等,2003;Anjyo,Lewis和Pighin,2014)。
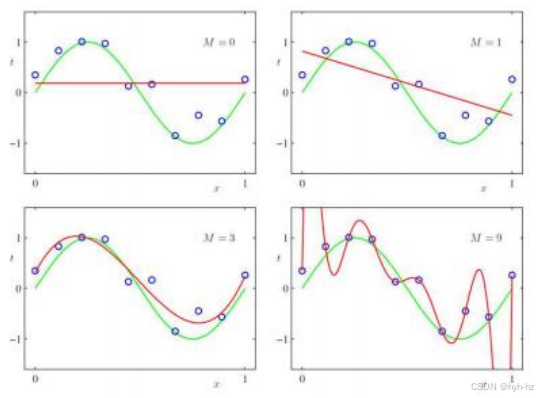
图4.3对蓝色圆圈进行多项式曲线拟合,这些圆圈是从绿色正弦曲线(Bishop2006)中获取的噪声样本。四个图表分别展示了零阶常数函数、一阶线性拟合、M = 3三次多项式以及九阶多项式。请注意,前两条曲线表现出欠拟合,而最后一条曲线则表现出过拟合,即过度波动。
当我们引入权重正则化(4.9)时,我们提到通常更倾向于近似数据,但没有解释原因。在大多数数据拟合问题中,样本dk(有时甚至是它们的位置xk )都是有噪声的,因此精确拟合是没有意义的。事实上,这样做可能会引入许多虚假的波动,而真实的解可能更加平滑。
为了深入探讨这一现象,让我们从一个简单的多项式拟合例子开始,该例子摘自(Bishop2006,第1.1章)。图4.3展示了多个不同阶数M的多项式曲线拟合到蓝色圆圈上,这些圆圈是从基础绿色正弦曲线上获取的噪声样本。请注意,低阶(M = 0和M = 1)的多项式严重欠拟合了基础数据,导致曲线过于平坦;而阶数M = 9的多项式则完全拟合了数据,但表现出远超实际可能的波动。
我们如何量化这种欠拟合和过拟合的程度,以及如何获得正确的程度?这个主题在机器学习中被广泛研究,并在许多文献中得到讨论。

图4.4对两个不同λ值的M = 9多项式拟合(Bishop 2006)©2006 Springer。左图显示了合理的正则化量,导致了合理的拟合,而右图中较大的λ值则导致了欠拟合。

图4.5拟合(训练)和验证误差与正则化或平滑量的关系©Glassner(2018)。右侧的正则化较少的解虽然具有较低的拟合误差,但在验证数据上的表现较差。
文献,包括Bishop (2006,第1.1章)、Glassner (2018,第9章)、Deisenroth、Faisal和Ong (2020,第8章)以及Zhang、Lipton等人(2021,第4.4.3节)。
一种方法是使用正则化最小二乘法,该方法在(4.11)中引入。图4.4展示了通过最小化(4.11)并使用多项式基函数φk (x) = xk得到的M = 9次多项式拟合,其中λ取了两个不同的值。左图显示了合理的正则化程度,导致了一个可信的拟合结果,而右图中较大的λ值则导致了欠拟合。请注意,图4.3右下角显示的M = 9插值对应于未正则化的λ = 0情况。
如果现在测量红色(估计)和绿色(无噪声)曲线之间的差异,我们会发现选择一个良好的中间值λ将产生最好的结果。

图4.6更加正则化的解log λ = 2.6显示出更高的偏差(偏离原始曲线),而较少正则化的版本(log λ = -2.4)则具有更高的方差(Bishop 2006)©2006斯普林格。左侧的红色曲线是基于绿色曲线上随机采样的25个点进行的M = 24高斯基拟合。右侧的红色曲线是这些拟合值的平均值。
然而,在实践中,我们从未获得过无噪声数据的样本。
相反,如果我们有一组样本需要插值,可以将其中的一部分保存在验证集中,以观察我们计算出的函数是欠拟合还是过拟合。当我们改变某个参数如λ(或使用其他指标来控制平滑度)时,通常会得到如图4.5所示的曲线。在这张图中,蓝色曲线表示拟合误差,在这种情况下称为训练误差,因为在机器学习中,我们通常会将给定的数据分为一个(通常是较大的)训练集和一个(通常是较小的)验证集。
为了更准确地估计理想的正则化量,我们可以多次重复将样本数据分割成训练集和验证集的过程。一种广为人知的技术称为交叉验证(Craven和Wahba 1979;Wahba和Wendelberger 1980;Bishop 2006,第1.3节;Murphy 2012,第1.4.8节;Deisenroth、Faisal和Ong 2020,第8章;Zhang、Lipton等2021,第4.4.2节),将训练数据分成K个部分(大小相等的部分)。然后依次保留每个部分,用剩余的数据进行训练。
数据。然后,你可以通过平均所有K次训练运行的结果来估计最佳正则化参数。虽然这种方法通常效果很好(K=5),但在训练大型神经网络时可能会过于昂贵,因为涉及的训练时间很长。
交叉验证只是模型选择技术的一个例子,这类技术通过在训练算法中估计超参数来实现良好的性能。其他方法包括信息准则,如贝叶斯信息准则(BIC)(Torr2002)和赤池信息准则(AIC)(Kanatani1998),以及贝叶斯建模方法(Szeliski1989;Bishop2006;Murphy2012)。
关于数据拟合,还有一个值得提及的话题,因为它经常出现在统计机器学习技术的讨论中,那就是偏差-方差权衡(Bishop 2006,第3.2节)。如图4.6所示,使用大量正则化(上排)会导致不同随机样本解之间的方差显著降低,但远离真实解的偏差却大幅增加。使用不足的正则化会急剧增加方差,尽管在大量样本上的平均值具有较低的偏差。关键在于确定一个合理的正则化折衷点,使得任何单个解都有接近真实情况(原始干净连续)数据的良好期望。
当我们对(4.9)中的权重添加一个正则化项时,我们注意到它不一定是二次惩罚,也可以是一个低阶单项式,以鼓励权重的稀疏性。
同样的想法可以应用于数据项,如(4.2),其中,我们可以使用一个稳健的损失函数P(),而不是使用二次惩罚,
k = f - dk;
这会降低较
数据拟合误差的权重,而较大的数据拟合误差更可能是异常测量值。(拟合误差项rk称为残差误差。)
图4.7展示了来自(Barron2019)的一些损失函数及其导数。常规的二次惩罚(α = 2)对每个误差给予完全(线性)权重,而α = 1损失则对所有较大的残差赋予相等的权重,即对于大残差表现为L1损失,而对于小残差则表现为L2损失。更大的α值会进一步减少大误差(异常值)的影响,尽管这会导致非凸优化问题,即可能存在多个局部最小值。我们将在第8.1.4节中讨论如何找到这些问题的良好初始猜测方法。

图4.7不同形状参数α值下的通用自适应损失函数(左)及其梯度(右)(Barron2019)©2019 IEEE。多个α值重现了现有的损失函数:L2损失(α = 2)、夏尔邦尼耶损失(α = 1)、柯西损失(α = 0)、盖曼-麦克卢尔损失(α = -2)和韦尔施损失(α = -1)。
在统计学中,最小化非二次损失函数以处理潜在的异常测量值被称为M估计(Huber1981;Hampel、Ronchetti等人1986;Black和Rangarajan1996;Stewart1999)。这类估计问题通常通过迭代重加权最小二乘法来解决,我们将在第8.1.4节和附录B.3中详细讨论。附录还讨论了稳健统计与非高斯概率模型之间的关系。
巴伦(2019)引入的广义损失函数有两个自由参数。第一个参数α控制异常值残差被大幅减权重的程度。第二个(尺度)参数c则控制最小值附近二次井的宽度,即残差值大致对应于内点的范围。传统上,α的选择是基于异常值分布的预期形状和计算考虑(例如是否需要凸损失)而启发式确定的,这与多种已发表的损失函数相对应。尺度参数c可以使用稳健的方差度量来估计,具体讨论见附录B.3。
在他的论文中,Barron(2019)讨论了如何通过最大化给定残差的似然性(或等效地,最小化负对数似然性)在运行时确定这两个参数,使这样的算法能够自我调整到各种噪声水平和

图4.8一个简单的表面插值问题:(a)九个不同高度的数据点散布在一个网格上;(b)二阶、受控连续性、薄板样条插值器,其左侧有一条撕裂线,右侧有一条折痕(Szeliski1989)©1989斯普林格。
我们在前一节介绍的正则化理论最初是由统计学家开发的,他们试图将模型拟合到严重限制解空间的数据(Tikhonov和Arsenin 1977;Engl、Hanke和Neubauer 1996)。例如,考虑找到一个平滑的表面,使其通过(或接近)一组测量数据点(图4.8)。这样的问题被称为不适定问题,因为许多可能的表面都可以拟合这些数据。由于输入的小变化有时会导致拟合结果的大变化(例如,如果我们使用多项式插值),这类问题通常也是病态的。由于我们试图从数据点d(xi,yi)中恢复未知函数f(x,y),这些问题也常被称为逆问题。许多计算机视觉任务可以视为逆问题,因为我们试图从有限的图像集中恢复三维世界的完整描述。
在前一节中,我们使用放置在数据点上的基函数或其他启发式方法,如拉推算法来解决这个问题。虽然这些技术可以提供合理的解决方案,但它们无法直接量化并优化解决方案的平滑度,也无法让我们局部控制解决方案在哪些地方应该不连续(图4.8)。
为了实现这一点,我们使用函数导数的范数(如下所述)来构建问题,然后找到这些范数的最小能量解。这类技术通常被称为基于能量或基于优化的方法。由于我们可以利用变分法来寻找最优解,因此它们也常被称为变分方法。自早期以来,变分方法已在计算机视觉中得到广泛应用。
20世纪80年代,提出并解决了许多基础问题,包括光流(霍恩和舒克1981;布莱克和阿南丹1993;布罗克斯、布鲁恩等人2004;维尔伯格、波克和比肖夫2010),分割(卡斯、威特金和特佐普洛斯1988;芒福德和沙赫1989;陈和维塞2001),去噪(鲁丁、奥舍尔和法特米1992;陈、奥舍尔和沈2001;陈和沈2005),以及多视图立体(福加拉斯和克里文1998;庞斯、克里文和福加拉斯2007;科列夫、克洛德等人2009)。更多相关论文列表可参见本章末尾的附加阅读部分。
为了量化找到一个平滑解的意义,我们可以在解空间上定义一个范数。对于一维函数f (x),我们可以积分该函数的一阶导数的平方,
(4.16)
或者整合平方的二阶导数,
(4.17)
(这里,我们用下标来表示微分。)这种能量度量是泛函的例子,泛函是将函数映射到标量值的算子。它们也常被称为变分法,因为它们测量的是函数的变化(非光滑性)。
在二维空间中(例如,对于图像、流场或表面),相应的平滑度函数为 (4.19)
其中混合的2fy项是需要使测量旋转不变的(Grimson 1983).
一阶导数范数常被称为膜,因为使用这种度量插值一组数据点会产生类似帐篷的结构。(实际上,这个公式是表面面积的小偏转近似,而肥皂泡正是最小化表面面积。)二阶范数称为薄板样条,因为它近似了薄板(例如柔性钢)在小变形下的行为。两者的结合称为张力下薄板样条(Terzopoulos1986b)。
我们刚才描述的正则化函数(平滑函数)迫使解在所有地方都是平滑的和C0和/或C1连续的。然而,在大多数计算机视觉应用中,我们试图建模或恢复的场只是分段连续的,例如,
深度图和光流场在物体不连续处跳跃。彩色图像更加不连续,因为它们在反照率(表面颜色)和阴影不连续处也改变外观。
为了更好地模拟这些函数,Terzopoulos(1986b)引入了受控连续性
样条,其中每个导数项都乘以一个局部加权函数,
+ τ (x, y)[fx (x, y) + 2fy (x, y) + fy (x, y)]} dx dy. (4.20)
在这里,P(x,y)∈[0,1]控制表面的连续性,而τ(x,y)∈[0,1]控制局部张力,即表面希望有多平坦。图4.8展示了一个简单的受控连续性插值器拟合九个散点数据的例子。实际上,更常见的是在图像和流场中使用一阶平滑项(第9.3节),而在表面中则使用二阶平滑项(第13.3.1节)。
除了平滑项之外,变分问题还需要一个数据项(或数据惩罚)。对于散点数据插值(Nielson1993),数据项测量函数f (x,y)与一组数据点di = d(xi,yi)之间的距离,
(4.21)
对于像噪声消除这样的问题,可以使用这种度量的连续版本,
εD = ∫ [f (x, y) - d (x, y)]2 dx dy. (4.22)
ε = εD + λεS , (4.23)
其中εS是平滑惩罚项(ε1、ε2或某种加权混合如εCC),λ是正则化参数,用于控制解的平滑度。正如我们在第4.1.2节中所见,可以通过交叉验证等技术估算出正则化参数的良好值。
为了找到这个连续问题的最小值,通常首先在规则网格上对函数f (x,y)进行离散化。2执行这种离散化的最合理的方法是使用
2使用以数据点为中心的核基函数的替代方案(Boult和Kender1986;Nielson
1993)在第13.3.1节中进行了更详细的讨论。
有限元分析,即用分段连续样条近似函数,然后进行解析积分(Bathe2007)。
幸运的是,对于一阶和二阶平滑函数,明智地选择适当的有限元可以得到特别简单的离散形式(Terzopoulos1983)。相应的离散平滑能量函数变为
(4.24)
+ sy(i,j)[f(i,j + 1)- f(i,j)- gy(i,j)]2
和+ 2cm(i,j)[f(i + 1,j + 1)- f(i + 1,j)- f(i,j + 1)+ f(i,j)]2 (4.25)
+ cy(i,j)[f(i,j + 1)- 2f(i,j)+ f(i,j - 1)]2,
其中h是有限元网格的大小。只有当能量在多种分辨率下被离散化时,如粗到细或多重网格技术中,h因子才重要。
可选的平滑权重sx(i,j)和sy(i,j)控制表面水平和垂直撕裂(或弱点)的位置。对于其他问题,如色彩化(Levin、Lischinski和Weiss 2004)和交互式色调映射(Lischinski、Farbman等2006),它们控制插值色度或曝光场的平滑度,并通常与局部亮度梯度强度成反比设置。对于二阶问题,折痕变量cx(i,j)、cm(i,j)和cy(i,j)控制表面折痕的位置(Terzopoulos 1988;Szeliski 1990a)。
数据值gx (i,j)和gy (i,j)是算法使用的梯度数据项(约束条件),例如光度立体(第13.1.1节)、HDR色调映射(第10.2.1节)(Fattal、Lischinski和Werman 2002)、泊松混合(第8.4.4节)(P rez、Gangnet和Blake 2003)、梯度
混合(第8.4.4节)(Levin、Zomet等人2004)和泊松表面重建(第13.5.1节)(Kazhdan、Bolitho和Hoppe 2006;Kazh- dan和Hoppe 2013)。当仅离散化常规的一阶平滑函数(4.18)时,这些值被设为零。请注意,在x、y和混合方向上可以分别施加平滑度和曲率项,以产生局部撕裂或折痕(Terzopoulos 1988;Szeliski 1990a)。
(4.26)
其中,局部置信权重c(i,j)控制数据约束的强制强度。当没有数据时,这些值被设为零;如果有数据,则可以设置为数据测量值的逆方差(如Szeliski(1989)所讨论及第4.3节所述)。
E = ED + λES = xTAx - 2xTb + c, (4.27)
其中x = [f(0,0)... f(m - 1,n - 1)]称为状态向量。
稀疏对称正定矩阵A被称为海森矩阵,因为它编码了能量函数的二阶导数。对于一维的一阶问题,A是三对角的;对于二维的一阶问题,它是多带状的,每行有五个非零元素。我们称b为加权数据向量。最小化上述二次型等价于求解稀疏线性系统。
Ax = b, (4.28)
这可以通过多种稀疏矩阵技术实现,例如多重网格(Briggs、Henson和McCormick 2000)和层次预处理器(Szeliski 2006b;Krishnan和Szeliski 2011;Krishnan、Fattal和Szeliski 2013),具体方法见附录A.5并在图4.11中展示。使用这些技术对于获得合理的运行时间至关重要,因为适当预处理的稀疏线性系统具有与像素数量呈线性的收敛时间。
虽然正则化最初由Poggio、Torre和Koch(1985)以及Terzopoulos(1986b)引入视觉领域,用于表面插值等问题,但很快被其他视觉研究人员广泛采用,应用于边缘检测(第7.2节)、光流(第9.3节)和阴影形状(第13.1节)等多样问题(Poggio、Torre和Koch 1985;Horn和Brooks1986;Terzopoulos1986b;Bertero,Poggio,Torre 1988;Brox、Bruhn等2004)。Poggio、Torre和Koch(1985)还展示了如何在电阻网格中实现由公式(4.24–4.26)定义的离散能量,如图4.9所示。在计算摄影(第10章)中,正则化及其变体常用于解决高动态范围色调映射(Fattal、Lischinski和Werman 2002;Lischinski、Farbman等2006)、泊松域和梯度域融合(P rez、Gangnet和Blake 2003;Levin、Zomet等2004;Agarwala、Dontcheva等。
3我们使用x代替f,因为这是数值分析文献中更常见的形式(Golub和Van Loan1996)。
在数值分析中,A被称为系数矩阵(Saad2003);在有限元分析中(Bathe2007),它被称为刚度矩阵。

图4.9一阶正则化的图形模型解释。白色圆圈表示未知数f(i,j),而深色圆圈表示输入数据d(i,j)。在电阻网格解释中,d和f值编码输入和输出电压,黑色方块表示电阻器,其导电性分别设为sx(i,j),sy(i,j),以及c(i,j)。在弹簧-质量系统类比中,圆圈表示高度,黑色方块表示弹簧。同样的图形模型也可用于描绘一阶马尔可夫随机场(图4.12)。
2004年),着色(Levin,Lischinski,and Weiss2004),以及自然图像遮罩(Levin,Lischinski,and Weiss2008)。
虽然正则化通常使用二次(L2)范数来表述,即公式(4.16–4.19)中的平方导数和公式(4.24–4.25)中的平方差,但也可以使用非二次鲁棒惩罚函数来表述,这些函数最早由Section4.1.3and提出,并在附录B.3中详细讨论。例如,(4.24)可以推广为
(4.29)
+ sy(i,j)P(f(i,j + 1)- f(i,j)),
其中P(x)是某个单调递增的惩罚函数。例如,范数族P(x) = jxjp被称为p-范数。当p < 2时,所得的平滑项比完全平滑更具有分段连续性,这可以更好地模拟图像、流场和三维表面的不连续特性。
鲁棒正则化的早期例子是Blake和Zisserman(1987)的渐进非凸性(GNC)算法。在这里,数据和导数上的范数是
P(x) = min(x2,V)。 (4.30)
由于所得问题高度非凸(存在多个局部最小值),提出了一种连续化方法,其中逐渐用非凸鲁棒范数(Allgower和Georg 2003)替代二次范数(该范数是凸的)。(大约同一时期,Terzopoulos(1988)也在使用连续化方法推断其表面插值问题中的撕裂和折痕变量。)
今天,许多正则化问题使用L1(p = 1)范数来表述,通常称为全变差(Rudin,Osher和Fatemi 1992;Chan,Osher和Shen 2001;Chambolle 2004;Chan和Shen 2005;Tschumperl和Deriche2005;Tschumperl2006;Cremers 2007;Kaftory,Schechner和Zeevi 2007;Kolev,Klodt等2009;Werlberger,Pock和Bischof 2010)。这种范数的优点在于它能更好地保留不连续性,但仍然产生一个具有全局唯一解的凸问题。其他范数,其影响(导数)更快地衰减至零,由Black和Rangarajan(1996)、Black,Sapiro等(1998)和Barron(2019)提出,并在第4.1.3节和附录B.3中讨论。
最近,当p < 1时的超拉普拉斯范数越来越受欢迎。这一观点基于图像导数的对数似然分布呈现出p≈0.5到0.8的斜率,因此属于超拉普拉斯分布(Simoncelli1999;Levin和Weiss2007;Weiss和Freeman2007;Krishnan和Fergus2009)。这类范数更倾向于偏好大的不连续性而非小的不连续性。详见第4.3节(4.43)。
虽然使用L2范数的最小二乘正则化问题可以通过线性系统求解,但其他p-范数需要不同的迭代技术,例如迭代重加权最小二乘法(IRLS)、Levenberg-Marquardt、局部非线性子问题与全局二次正则化之间的交替(Krishnan和Fergus2009),或原对偶算法(Chambolle和Pock2011)。这些技术在第8.1.3节和附录A.3和B.3中讨论。
在我们对变分方法的讨论中,我们关注的是基于梯度和高阶导数的能量最小化问题,在离散设置中涉及
评估相邻像素之间的加权误差。正如我们在第3.3.2节讨论双边滤波时所见,通过查看更大的空间邻域并结合颜色或灰度值相似的像素,我们通常可以获得更好的结果。为了将这一想法扩展到变分(能量最小化)设置中,Barron和Poole(2016)提出用更广泛的邻域双边加权版本替代常用的最邻近平滑惩罚(4.24)。
(4.31)
在哪里
(4.32)
是双边权重函数(3.37)的双随机化(归一化)版本,可能依赖于输入引导图像,但不依赖于f的估计值。5
为了高效地求解这组方程(比最近邻版本密集得多),作者采用了最初用于加速双边滤波的方法,即在(空间上较粗略的)双边网格上求解相关问题。操作序列类似于双边滤波中使用的,只是在拼接后和切片前,使用了迭代最小二乘法求解器而不是多维高斯模糊。为了进一步加快共轭梯度求解器的速度,Barron和Poole(2016)采用了一种受先前图像自适应预处理器研究启发的多级预处理器(Szeliski2006b;Krishnan、Fattal和Szeliski2013)。
自引入以来,双边求解器已在多种视频处理和三维重建应用中使用,包括双目全景视频的拼接(Anderson,Gallup等,2016)。Valentin、Kowdle等(2018)开发的智能手机增强现实系统扩展了双边求解器,使其具有局部平面模型,并采用硬件友好的实时实现(Mazumdar,Alaghi等,2017),以生成密集的遮挡效果。
边缘感知插值技术在色彩化中的应用非常出色,即手动为“黑白”(灰度)图像添加颜色。在大多数色彩化的应用中,用户会在某些区域画出一些涂鸦,指示所需的颜色(图4.10a),系统则将指定的色度(u,v)值插值到整个图像中,从而实现色彩化效果。
5注意,在他们的论文中,Barron和Poole(2016)对像素颜色差异的亮度和色度分量使用了不同的σr值。

图4.10使用优化进行着色(Levin,Lischinski和Weiss 2004)©2004 ACM:(a)灰度图像上叠加了一些彩色涂鸦;(b)最终的着色图像;(c)原始彩色图像,从中提取了灰度图像和涂鸦的色度值。原始照片由Rotem Weiss拍摄。
然后与输入的亮度通道重新组合,生成最终的彩色图像,如图4.10b所示。在Levin、Lischinski和Weiss(2004)开发的系统中,插值使用局部加权正则化(4.24),其中局部平滑权重与亮度梯度成反比。这种局部加权正则化的方法启发了后来用于高动态范围色调映射的算法(Lischinski、Farbman等,2006)(第10.2.1节,以及其他加权最小二乘法(WLS)公式的应用(Farbman、Fattal等,2008)。这些技术从图像适应的正则化技术中受益匪浅,例如Szeliski(2006b)、Krishnan和Szeliski(2011)、Krishnan、Fattal和Szeliski(2013)以及Barron和Poole(2016)所开发的技术,如图4.11所示。Yatziv和Sapiro(2006)还开发了一种基于测地线(边缘感知)距离函数的稀疏色度插值替代方法。神经网络也可以用于实现图像色彩化的深度先验(Zhang、Zhu等,2017)。
正如我们刚刚所见,正则化涉及最小化定义在(分段)连续函数上的能量泛函,可以用于构建和解决各种低级别的计算机视觉问题。另一种技术是构建贝叶斯或生成模型,该模型分别建模噪声图像形成(测量)过程,并假设解空间的统计先验模型(Bishop2006,第1.5.4节)。在本节中,我们将探讨基于马尔可夫随机场的先验,其对数似然可以用局部邻域交互(或惩罚)项来描述(Kin-

图4.11使用局部适应的层次基预处理加速非齐次最小二乘着色求解器(Szeliski2006b)©2006 ACM:(a)输入带有彩色笔触的灰度图像;(b)共轭梯度迭代20次后的解;(c)使用一次层次基函数预处理;(d)使用一次局部适应的层次基函数。
德曼和斯内尔1980;Geman和Geman1984;Marroquin、Mitter和Poggio1987;Li 1995;Szeliski、Zabih等人2008;Blake、Kohli和Rother2011)。
贝叶斯建模相较于正则化有许多潜在优势(详见附录B)。能够对测量过程进行统计建模,使我们能够从每次测量中提取尽可能多的信息,而不仅仅是猜测数据的权重。同样地,通过观察我们所建模类别的样本,通常可以学习先验分布的参数(Roth和Black 2007a;Tappen 2007;Li和Huttenlocher 2008)。此外,由于我们的模型是概率性的,原则上可以估计未知变量的完整概率分布,特别是可以建模解中的不确定性,这在后续处理阶段非常有用。最后,马尔可夫随机场模型可以在离散变量上定义,例如图像标签(其中变量没有适当的顺序),在这种情况下,正则化不适用。
根据贝叶斯规则(附录B.4),给定测量值y,未知数x的后验分布p(xjy)可通过将测量似然p(yjx)乘以先验分布p(x)并进行归一化得到,
其中,p(y) =,xp(yjx)p(x)是一个归一化常数,用于使p(xjy)分布适于(积分为1)。取(4.33)的两边的负对数,我们得到
- log p(xjy)= - log p(yjx)- log p(x) + C; (4.34)是负后验对数似然。
为了找到给定一些测量值y的最可能(最大后验概率或MAP)解x,我们只需最小化这个负对数似然,这也可以被认为是一种能量,
E (x, y) = ED (x, y) + EP (x). (4.35)
(我们省略常数C,因为在能量最小化过程中其值无关紧要。)第一项ED(x,y)是数据能量或数据惩罚;它衡量了给定未知状态x时观察到数据的负对数似然。第二项EP (x)是先验能量;它的作用类似于正则化中的平滑能量。请注意,最大后验概率估计可能并不总是理想的选择,因为它选择了后验分布中的“峰值”,而不是某个更稳定的统计量——参见附录B.2以及Levin、Weiss等人(2009)的讨论。
在本节的剩余部分,我们将重点关注马尔可夫随机场,这是一种定义在二维或三维像素或体素网格上的概率模型。然而,在深入探讨之前,我们应当指出,MRFs只是更广泛的图形模型家族中的一个特例(Bishop2006,第8章;Koller和Friedman2009;Nowozin和Lampert2011;Murphy2012,第10、17、19章),这些模型具有变量之间的稀疏交互关系,可以在因子图中捕捉到(Dellaert和Kaess2017;Dellaert 2021),如图4.12所示。图形模型有多种拓扑结构,包括链式(用于音频和语音处理)、树形(常用于建模跟踪人物时的运动链(例如,Felzenszwalb和Huttenlocher2005))、星型(简化的人物模型;Dalal和Triggs2005;Felzenszwalb、Girshick等人2010)以及星座(Fergus、Perona和Zisserman2007)。这些模型广泛用于基于部件的识别,如第6.2.1节所述。对于无环图,可以使用基于动态规划的有效线性时间推断算法。
对于图像处理应用,未知数x是输出像素的集合
x = [f(0, 0) . . . f (m - 1, n - 1)], (4.36)
数据(在最简单的情况下)是输入像素
y = [d(0, 0) . . . d(m - 1, n - 1)] (4.37)
如图4.12所示。
对于一个马尔可夫随机场,概率p(x)是一个吉布斯或玻尔兹曼分布,其负对数似然(根据哈默斯利-克利福德定理)可以写成成对相互作用势的总和,

图4.12 N4邻域马尔可夫随机场的图形模型。(蓝色边表示N8邻域。)白色圆圈是未知数f(i,j),深色圆圈是输入数据d(i,j)。sx(i,j)和sy(i,j)黑色框表示随机场中相邻节点之间的任意交互势,c(i,j)表示数据惩罚函数。相同的图形模型也可用于描绘一阶正则化问题的离散版本(图4.9)。
其中N(i,j)表示像素(i,j)的邻居。实际上,该定理的一般版本指出,能量可能需要在一个更大的团集集合上进行评估,这取决于马尔可夫随机场的顺序(Kindermann和Snell 1980;Geman和Geman 1984;Bishop 2006;Kohli、Ladick和Torr 2009;Kohli、Kumar和Torr 2009)。
在马尔可夫随机场模型中最常用的邻域是N4邻域,在该邻域中,场f(i,j)中的每个像素仅与其直接相邻的像素相互作用。图4.12所示的模型,我们之前在图4.9中用于说明一阶正则化的离散版本,展示了一个N4 MRF。sx(i,j)和sy(i,j)的黑框表示随机场中相邻节点之间的任意交互势,而c(i,j)表示数据惩罚函数。这些方形节点也可以解释为因子图版本中的因子(无向)图形模型(Bishop 2006;Dellaert和Kaess 2017;Dellaert 2021),这是交互势的另一种名称。(严格来说,这些因子是(不正规的)概率函数,它们的乘积是(未归一化)后验分布。)
正如我们将在(4.41–4.42)中看到的,这些相互作用势与正则化图像恢复问题的离散版本之间存在密切关系。因此,初步来看,当解决正则化问题时进行的能量最小化与在MRF中执行的最大后验推断是等价的。
虽然N4邻域最常用,但在某些应用中,N8(甚至更高阶)邻域在图像分割等任务上表现更好,因为它们可以更好地建模不同方向的不连续性(Boykov和Kolmogorov2003;Rother、Kohli等人2009;Kohli、Ladick和Torr2009;Kohli、Kumar和Torr2009)。
最简单的马尔可夫随机场的例子是二进制场。这种场的例子包括1位(黑白)扫描文档图像以及分割成前景和背景区域的图像。
为了对扫描图像进行去噪,我们将数据惩罚设置为反映扫描图像和最终图像之间的一致性,
ED (i, j) = wδ(f(i, j), d(i, j)) (4.39)
以及平滑惩罚,以反映相邻像素之间的协议
EP(i,j)= sδ(f(i,j),f(i + 1,j))+ sδ(f(i,j),f(i,j + 1))。 (4.40)
一旦我们确定了能量,如何将其最小化?最简单的方法是执行梯度下降,每次只改变一个状态,如果该状态能产生更低的能量。这种方法被称为上下文分类(Kittler和Fo...glein 1984)、迭代条件模式(ICM)(Besag 1986),或者最高置信度优先(HCF)(Chou和Brown 1990),前提是首先选择能量减少最大的像素。
不幸的是,这些下坡方法容易陷入局部最小值。一种替代方法是在过程中加入一些随机性,这被称为随机梯度下降(Metropolis,Rosenbluth等1953;Geman和Geman 1984)。当噪声量随时间减少时,这种技术被称为模拟退火(Kirkpatrick,Gelatt和Vecchi 1983;Carnevali,Coletti和Patarnello 1985;Wolberg和Pavlidis 1985;Swendsen和Wang 1987),最初由Geman和Geman(1984)在计算机视觉领域推广,后来被Barnard(1989)等人应用于立体匹配。
即使这种技术,效果也不尽如人意(Boykov,Veksler,和Zabih 2001)。对于二值图像,Boykov、Veksler和Zabih(2001)向计算机视觉社区介绍了一种更好的方法,即将能量最小化问题重新表述为最大流/最小割图优化问题(Greig,Porteous,和Seheult 1989)。这一技术在计算机视觉界非正式地被称为图割(Boykov和Kolmogorov 2011)。对于简单的能量函数,例如非相同邻近像素的惩罚为常数的情况,该算法可以保证产生
全局最小值。柯尔莫哥洛夫和扎比(2004)正式定义了这些结果成立的二元能量势类(正则条件),而科莫达基斯、齐里塔斯和帕拉吉奥斯(2008)以及罗瑟、柯尔莫哥洛夫等人(2007)的新研究则提供了良好的算法,用于处理这些条件不成立的情况,即能量函数不是正则或次模的情况。
除了上述技术外,还开发了多种优化方法用于MRF能量最小化,例如(循环)信念传播和动态规划(针对一维问题)。这些内容在附录B.5中进行了更详细的讨论,以及Szeliski、Zabih等人(2008年)和Kappes、Andres等人(2015年)的比较综述论文,它们在https: //vision.middlebury.edu/MRF和http://hciweb2.iwr.uni-heidelberg.de/opengm上提供了相关的基准测试和代码。
除了二值图像外,马尔可夫随机场还可以应用于有序值标签,如灰度图像或深度图。“有序”一词表明标签具有隐含的顺序,例如,较高的值表示较亮的像素。在下一节中,我们将探讨无序标签,如用于图像合成的源图像标签。
ED(i,j)= c(i,j)Pd(f(i,j)- d(i,j)) (4.41)
EP(i,j)= sx(i,j)Pp(f(i,j)- f(i + 1,j))+ sy(i,j)Pp(f(i,j)- f(i,j + 1)),(4.42)
这些是二次惩罚项(4.26)和(4.24)的稳健推广,首次引入于(4.29)。与之前一样,c(i,j),sx(i,j),sy(i,j)的权重可用于局部控制数据加权以及水平和垂直平滑度。然而,这里使用的是一个一般的单调递增惩罚函数P(),而不是二次惩罚。(数据项和平滑度项可以使用不同的函数。)例如,Pp可以是一个超拉普拉斯惩罚。
Pp (d) = jdjp , p < 1, (4.43)
与二次或线性(总变差)惩罚相比,它能更好地编码图像中梯度(主要是边缘)的分布。6 Levin和Weiss(2007)使用这样的惩罚
6注意,与二次惩罚不同,水平和垂直导数的p-范数之和不是旋转不变的。更好的方法可能是局部估计梯度方向,并对垂直和平行分量施加不同的范数,Roth和Black(2007b)称之为可转向随机场。

图4.13灰度图像去噪和修复:(a)原始图像;(b)图像
被噪声破坏且数据缺失(黑色条);(c)使用循环信念传播恢复的图像;(d)使用扩展移动图切割恢复的图像。这些图像是来自https: //vision.middlebury.edu/MRF/results (Szeliski,Zabih等人,2008年)。
通过鼓励梯度位于一个或另一个图像中,而不是同时位于两个图像中,来分离传输和反射的图像(图9.16)。Levin等人(2007)使用超拉普拉斯作为图像去卷积(去模糊)的先验,而Krishnan和Fergus(2009)则开发了一种更快的算法来解决此类问题。对于数据惩罚,ρd可以是二次的(用于建模高斯噪声)或受污染高斯的对数(附录B.3)。
当ρp是一个二次函数时,生成的马尔可夫随机场被称为高斯马尔可夫随机场(GMRF),其最小值可以通过稀疏线性系统求解(4.28)找到。当权重函数均匀分布时,GMRF成为维纳滤波的一个特例(第3.4.1节)。允许权重函数依赖于输入图像(一种特殊的条件随机场,我们将在下文描述)可以实现相当复杂的图像处理算法,包括色彩化(Levin、Lischinski和Weiss 2004年)、交互式色调映射(Lischinski、Farbman等2006年)、自然图像抠图(Levin、Lischinski和Weiss 2008年)以及图像修复(Tappen、Liu等2007年)。
当ρd或ρp是非二次函数时,可以使用非线性最小二乘法或迭代重加权最小二乘法等梯度下降技术(附录A.3)。然而,如果搜索空间存在大量局部最小值,如立体匹配的情况(Barnard1989;Boykov,Veksler,和Zabih2001),则需要更复杂的技术。
图割技术扩展到多值问题首先由Boykov、Veksler和Zabih(2001)提出。在他们的论文中,他们开发了两种不同的算法,称为交换移动和扩展移动,它们在一系列二进制标记之间迭代。

图4.14来自Boykov、Veksler和Zabih(2001)的多层图优化©2001 IEEE: (a)初始问题配置;(b)标准移动仅改变一个像素;(c)
α-β交换最优地交换所有α和β标记的像素;(d)α扩展移动在当前像素值和α标签之间进行最优选择。
子问题以找到一个好的解决方案(图4.14)。请注意,由于该问题是证明为NP难的,因此通常无法获得全局解。因为这两种算法在其内部循环中都使用了二进制MRF优化,所以它们受到与二进制标记情况下的能量函数约束相同的影响(Kolmogorov和Zabih 2004)。
另一种MRF推理技术是信念传播(BP)。虽然信念传播最初是在树结构上开发的,且在此类结构中它是精确的(Pearl1988),但最近它已被应用于包含环路的图,如马尔可夫随机场(Freeman,Pasztor和Carmichael2000;Yedidia,Freeman和Weiss2001)。事实上,一些性能较好的立体匹配算法使用环路信念传播(LBP)来进行推理(Sun,Zheng和Shum2003)。关于LBP的详细讨论可以在比较调查论文中找到,这些论文涉及MRF优化(Szeliski,Zabih等2008;Kappes,Andres等2015)。
图4.13展示了一个使用非二次能量函数(非高斯MRF)进行图像去噪和修复(孔洞填充)的例子。原始图像已被噪声破坏,部分数据被移除(黑色条)。在这种情况下,循环信念传播算法计算出的能量略低,且生成的图像更加平滑,优于α扩展图割算法。
当然,上述公式(4.42)中平滑项EP(i;j)仅展示了最简单的情况。在后续研究中,Roth和Black(2009)提出了一种专家领域(FoE)模型,该模型汇总了大量指数化的局部滤波器输出以得出平滑惩罚。Weiss和Freeman(2007)分析了这种方法,并将其与自然图像统计的更简单的超拉普拉斯模型进行了比较。Lyu和Simoncelli(2009)使用

图4.15具有更复杂度量的马尔可夫随机场的图形模型
模型。附加的彩色边表示未知值的组合(比如,在一幅清晰的图像中)产生测量值(一幅嘈杂模糊的图像)。所得的图-
经典MRF模型仍然是一个经典模型,从它中抽取样本同样容易,但可以进行一些推断
算法(例如基于图切割的算法)可能不适用,因为网络复杂性增加,因为在推理期间状态变化变得更加纠缠,后验MRF具有更大的团。
高斯尺度混合物(GSM)用于构建非均匀多尺度MRF,其中一个(正指数)GMRF调制另一个高斯MRF的方差(振幅)。
也可以扩展测量模型,使采样的(受噪声干扰的)输入像素对应于未知(潜在)图像像素的混合,如图4.15所示。这是尝试去模糊图像时常见的情况。虽然这种模型仍然是传统的生成马尔可夫随机场,即原则上可以从先验分布中生成随机样本,但由于团大小变大,找到最优解可能会很困难。在这种情况下,可以使用梯度下降技术,例如迭代重新加权最小二乘法(Joshi,Zitnick等,2009)。练习4.4让你探讨这些问题。
未排序的标签
另一个常应用马尔可夫随机场的多值标签案例是无序标签,即两个标签之间的数值差异没有语义意义的标签。例如,在从航拍图像中分类地形时,森林、田野、水域和人行道所分配标签之间的数值差异是没有意义的。事实上,这些不同类型的地形之间的相邻关系

图4.16无序标签MRF (Agarwala,Dontcheva (et al.2004)©2004 ACM:左侧每个源图像中的笔画被用作MRF优化的约束条件,该优化通过图割法求解。最终的多值标签场以颜色叠加的形式显示在中间图像中,最终合成图则显示在右侧。
每个都有不同的可能性,所以使用这种形式的先验更有意义
EP(i,j)= sx(i,j)V (l(i,j),l(i + 1,j))+ sy(i,j)V (l(i,j),l(i,j + 1)),(4.44)
其中V(l0,l1)是一个通用的兼容性或势函数。(请注意,我们还用l(i,j)替换了f(i,j),以更清楚地表明这些是标签而不是函数样本。)另一种表示这种先验能量的方法(Boykov,Veksler和Zabih 2001;Szeliski,Zabih等2008)是
(4.45)
其中(p,q)是相邻像素,并且为每对相邻像素评估空间变化的势函数Vp,q。
无序MRF标记的一个重要应用是在图像合成中的接缝检测(Davis 1998;Agarwala、Dontcheva等2004)(见图4.16,详见第8.4.2节)。在这里,兼容性Vp,q(lp,lq)衡量了将图像lp中的像素p放置在图像lq中的像素q旁边时,视觉效果的质量。与大多数马尔可夫随机场一样,我们假设Vp,q(l,l)= 0。然而,对于不同的标签,兼容性Vp,q(lp,lq)可能取决于底层像素Ilp (p)和Ilq (q)的值。
例如,考虑一个图像I0是全天蓝色的,即I0 (p) = I0 (q) = B,而另一个图像I1从天蓝色I1 (p) = B过渡到森林绿I1 (q) = G
I0 : p q p q : I1
在这种情况下,Vp,q(1,0)=0(颜色一致),而Vp,q(0,1)>0(颜色不一致)。
在经典贝叶斯模型(4.33–4.35)中,
p (xjy) α p (yjx)p (x), (4.46)
先验分布p(x)与观测值y无关。然而,有时根据感知到的数据调整我们的先验假设是有用的,比如关于我们要估计的场的平滑性。这种做法是否从概率角度合理,我们将在解释新模型后讨论。
考虑一个交互式图像分割系统,如博伊科夫和芬卡-利(2006)所描述的那样。在这个应用中,用户绘制前景和背景轮廓,系统随后解决一个二值MRF标记问题,以估计前景对象的范围。除了最小化数据项,该数据项衡量像素颜色与推断区域分布之间的逐点相似性(第4.3.2节),MRF还被修改,使得图4.12和公式(4.42)中的平滑项sx(x,y)和sy(x,y)依赖于相邻像素之间的梯度大小。7
由于平滑项现在依赖于数据,贝叶斯规则(4.46)不再适用。相反,我们使用后验分布p(xjy)的直接模型,其负对数似然可以表示为
E (xjy) = ED (x, y) + ES (x, y)
(4.47)
使用(4.45)中引入的符号。由此产生的概率分布称为条件随机场(CRF),最初由库马尔和赫伯特(2003)引入计算机视觉领域,基于拉弗蒂、麦考尔姆和佩雷拉(2001)在文本建模方面的早期工作。
图4.17显示了一个图形模型,其中平滑项取决于数据值。在这个特定的模型中,每个平滑项仅取决于其相邻的一对数据值,即,项的形式为Vp,q(xp,xq,yp,yq),如公式(4.47)所示。
根据输入数据修改平滑项的想法并不新鲜。例如,Boykov和Jolly(2001)将这一想法用于交互式分割,现在它被广泛应用于图像分割(第4.3.2节)(Blake、Rother等人,2004;Rother、Kolmogorov和Blake,2004),去噪(Tappen、Liu等人,2007)和物体识别(第6.4节)(Winn和Shotton,2006;Shotton、Winn等人,2009)。
7 Poggio、Gamble和Little(1988)提出了一种替代方案,该方案同样使用检测到的边缘来调节深度或运动场的平滑度,从而整合多个较低层次的视觉模块。

图4.17条件随机场(CRF)的图形模型。附加的绿色
边缘显示了感知数据组合如何影响底层MRF先验模型的平滑性,即公式(4.42)中的sx(i,j)和sy(i,j)依赖于相邻的d(i,j)值。这些额外的链接(因素)使得平滑性能够依赖于输入数据。然而,这使得从这个MRF中采样变得更加复杂。
在立体匹配中,鼓励视差不连续性与强度边缘相吻合的想法可以追溯到优化和基于MRF的算法的早期(Poggio、Gamble和Little1988;Fua1993;Bobick和Intille1999;Boykov、Veksler和Zabih2001),并在(第12.5节)中进行了更详细的讨论。
除了使用适应输入数据的平滑项外,库马尔和赫伯特(2003)还为每个Vp(xp,y)项计算了一个邻域函数,如图4.18所示,而不是使用图4.12.8中所示的经典一元MRF数据项Vp(xp,yp)。因为这样的邻域函数可以被视为判别函数(机器学习中广泛使用的术语(Bishop 2006)),他们将由此产生的图形模型称为判别随机场(DRF)。在他们的论文中,库马尔和赫伯特(2006)表明,在结构检测和二值图像去噪等应用中,DRFs优于类似的CRFs。
在这里,有人可能会认为之前的立体对应算法也考虑了输入数据的邻域,无论是显式地,因为它们计算相关度量(Criminisi,Cross等人2006)作为数据项,还是隐式地,因为即使是像素级视差成本也会查看左图或右图中的多个像素(Barnard 1989;Boykov,Veksler和Zabih 2001)。
那么使用条件或判别有什么优缺点呢
8 Kumar和Hebert(2006)将一元势能Vp(xp;y)称为关联势能,将成对势能Vp;q(xp;y q;y)称为相互作用势能。

图4.18辩别随机场(DRF)的图形模型。额外的绿色边表示感知数据的组合,例如d(i,j + 1),如何影响f(i,j)的数据项。因此,生成模型更为复杂,即我们不能简单地对未知变量应用一个函数并添加噪声。
随机场而不是MRF?
经典贝叶斯推断(MRF)假设数据的先验分布与测量无关。这很有道理:如果你第一次掷骰子时看到一对六,那么假设之后每次都会出现六是不明智的。然而,如果你长时间玩后发现统计上的显著偏差,你可能需要调整你的先验。CRF实质上就是根据观察到的数据选择或修改先验模型。这可以看作是对额外隐藏变量或未知量(如标签、深度或干净图像)与已知量(观察到的图像)之间的相关性进行部分推断。
在某些情况下,CRF方法非常合理,实际上是唯一可行的途径。例如,在灰度图像着色(第4.2.4节)(Levin、Lischinski和Weiss 2004)中,一种常见的方法是通过修改局部平滑约束来将连续性信息从输入的灰度图像传递到未知的颜色图像。同样地,在同时进行分割和识别时(Winn和Shotton 2006;Shotton、Winn等2009),允许强烈的颜色边缘以增加语义图像标签不连续性的可能性是非常合理的。
在其他情况下,如图像去噪,情况更为微妙。使用非二次(鲁棒)平滑项,如公式(4.42)所示,其定性作用类似于基于高斯MRF(GMRF)中的局部梯度信息来设置平滑度(Tappen,Liu等,2007;Tanaka和Okutomi,2008)。当平滑度能够正确推断时,高斯MRF的优势在于可以最小化由此产生的二次能量。

图4.19使用全连接CRF进行像素级分类,来自©Kr......ahenbuhl和Koltun(2011)。每列中的标签描述了正在运行的图像或算法,包括一个强大的Pn CRF (Kohli、Ladick和Torr 2009)和一个非常慢的MCMC优化算法。
在单一步骤中,即通过求解一组稀疏线性方程。然而,在输入数据中不连续性不是显而易见的情况下,例如分段平滑的稀疏数据插值(Blake和Zisserman 1987;Terzopoulos 1988),经典的鲁棒平滑能量最小化可能更为合适。因此,与大多数计算机视觉算法一样,需要仔细分析当前问题以及所需的鲁棒性和计算限制,以选择最佳技术。
或许,正如库马尔和赫伯特(2006)、塔彭、刘等人(2007)以及布莱克、罗瑟等人(2004)所论述的那样,CRF和DRF最大的优势在于学习模型参数更加有原则性,有时也更容易。虽然在MRF及其变体中学习参数不是本书讨论的主题,但感兴趣的读者可以在库马尔和赫伯特(2006)、罗斯和布莱克(2007a)、塔彭、刘等人(2007)、塔彭(2007)以及李和胡滕洛赫(2008)的出版物中找到更多详细信息。
密集条件随机场(CRF)
与常规的马尔可夫随机场一样,条件随机场(CRF)通常定义在小邻域上,例如图4.17所示的N4邻域。然而,图像通常包含较长距离的相互作用,例如,颜色相似的像素可能属于
相关类(图4.19)。为了模拟这种长距离交互,Kra......henbuhl和Koltun(2011)引入了他们称之为全连接CRF的模型,现在许多人称之为密集CRF。
与传统的条件随机场(4.47)一样,它们的能量函数由一元项和成对项组成
(4.48)
其中(p,q)求和现在是对所有像素对进行的,而不仅仅是相邻的像素。9 y表示随机场所依赖的输入(引导)图像。成对相互作用势具有受限形式
(4.49)
这是空间不变的标签兼容函数μ(xp,xq)和M个相同形式(3.37)的高斯核之和的产物,这些高斯核用于双边滤波和双边求解器。在他们的开创性论文中,Kra... ...hl和Koltunhenbu(2011)使用了两个核,第一个是类似于(3.37)的外观核,第二个是仅空间平滑核。
由于长程相互作用势的特殊形式,它将所有空间和颜色相似性项封装成双边形式,可以使用类似于快速双边滤波器和求解器中使用的高维滤波算法(Adams,Baek,和Davis 2010)来高效计算后验条件分布的平均场近似(Kra... ...hl和Koltunhenbu2011)。图4.19显示了他们的结果(最右一列)与先前方法的比较,包括使用简单的单项式,a
稳健的CRF(Kohli,Ladick和Torr2009),以及非常慢的MCMC(马尔可夫链蒙特卡洛
Carlo)推理算法。如您所见,全连接CRF与平均场求解器相结合,在很短的时间内就能产生显著更好的结果。
自本文发表以来,原作者(Kra等人)已经开发出可证明收敛和更有效的推理算法。 ...hl和Koltunhenbu2013)和其他人(Vineet,Warrell,和Torr2014;Desmaison,Bunel等人2016)。密集CRF在图像分割问题中得到了广泛应用,同时也作为深度神经网络的“清理”阶段,如陈、Papandreou等人(2018)广受引用的DeepLab论文所示。
图像分割算法的目标是将具有相似外观(统计特征)的像素聚类,并使不同区域之间的像素边界长度较短且跨越可见的不连续点。如果我们限制边界测量仅在相邻像素之间进行,并通过累加像素来计算区域隶属度统计,就可以将其表述为经典的基于像素的能量函数,可以使用变分形式(第4.2节)或二值马尔可夫随机场(第4.3节)。
连续方法的例子包括穆姆福德和沙(1989)、陈和维斯(2001)、朱和尤尔(1996)以及塔布和阿胡贾(1997),还有第7.3.2节中讨论的水平集方法。早期的一个离散标记问题的例子是勒克莱尔(1989)的工作,他结合了基于区域和边界的能量项,使用最小描述长度(MDL)编码来推导最小化的能量函数。博伊科夫和芬卡-利(2006)对各种基于能量的技术进行了精彩的综述,用于二值对象分割,其中一些技术我们在下面会讨论。
正如我们在本章前面所看到的,与分割问题相对应的能量可以写成(参见公式(4.24)和(4.35–4.42))
(4.50)
区域项
ER(i,j)= C(I(i,j);R(f(i,j))) (4.51)
是像素强度(或颜色)I(i,j)与区域R(f(i,j))的统计量一致的负对数似然和边界项
EP(i,j)= sx(i,j)δ(f(i,j),f(i + 1,j))+ sy(i,j)δ(f(i,j),f(i,j + 1))(4.52)
测量由局部水平和垂直平滑项sx (i,j)和sy (i,j)调制的N4邻居之间的不一致性。
区域统计可以是简单的平均灰度或颜色(Leclerc 1989),在这种情况下
C(I; μk ) = ⅡI - μk Ⅱ2 . (4.53)
或者,它们可以更复杂,例如区域强度直方图(Boykov和Jolly 2001)或颜色高斯混合模型(Rother、Kolmogorov和Blake 2004)。对于平滑度(边界)项,通常使平滑度强度sx(i,j)与局部边缘强度成反比(Boykov、Veksler和Zabih 2001)。
最初,基于能量的分割问题使用迭代梯度下降技术进行优化,这种方法速度慢,容易陷入局部最小值。

图4.20 GrabCut图像分割(Rother,Kolmogorov和Blake 2004)©2004 ACM:(a)用户用红色绘制边界框;(b)算法猜测物体和背景的颜色分布并进行二值分割;(c)重复此过程,使用更好的区域统计信息。
Jolly(2001)是第一个将Greig、Porteous和Seheult(1989)开发的二进制MRF优化算法应用于二进制对象分割。
在这种方法中,用户首先使用图像画笔在背景和前景区域勾勒出像素。这些像素随后成为连接S-T图节点与源点和汇点标签S和T的种子。种子像素还可以用于估计前景和背景区域的统计特性(如强度或颜色直方图)。
图中其他边的能力源自区域和边界能量项,即与前景或背景区域更兼容的像素会获得更强的连接到相应的源或汇;相邻像素若平滑度更高也会获得更强的链接。一旦使用多项式时间算法(Goldberg和Tarjan 1988;Boykov和Kolmogorov 2004)解决了最小割/最大流问题,计算出的割两侧的像素将根据它们仍连接的源或汇进行标记。尽管图割只是已知用于MRF能量最小化的几种技术之一,但它仍然是解决二进制MRF问题最常用的方法。
博伊科夫和乔利(2001)的基本二值分割算法已在多个方向上得到了扩展。罗瑟、科尔莫戈罗夫和布莱克(2004)的GrabCut系统通过迭代重新估计区域统计信息,这些统计信息在颜色空间中被建模为高斯混合模型。这使得他们的系统能够在最少用户输入的情况下运行,例如单个边界框(图4.20a)——背景颜色模型从框轮廓周围的像素条初始化。(前景颜色模型从内部像素初始化,但很快收敛到更准确的对象估计。)用户还可以放置额外的笔画以在解决方案过程中细化分割。崔、杨等人(2008)利用从类似对象的先前分割中派生的颜色和边缘模型来改进GrabCut中使用的局部模型。图割算法和其他变体的马尔可夫和条件

图4.21使用有向图切割进行分割(Boykov和Funka-Lea 2006)©2006斯普林格:(a)有向图;(b)带有种子点的图像;(c)无向图错误地沿亮物体继续边界;(d)有向图正确地将浅灰色区域与其较暗的背景分离。
随机场已应用于语义分割问题(Shotton,Winn等人,2009年;Kra... ...hl和Koltunhenbu2011),图4.19给出了一个例子,我们将在第6.4节中详细研究。
另一个对原始二值分割公式的主要扩展是增加了有向边,这使得边界区域可以被定向,例如,偏好从亮到暗的过渡或反之(Kolmogorov和Boykov 2005)。图4.21显示了一个例子,其中有向图割正确地将浅灰色肝脏与其深灰色背景分离。同样的方法也可以用于测量从一个区域流出的通量,即垂直于区域边界的带符号梯度投影。结合有向图和更大的邻域,可以在全局最优图割框架中近似解决连续问题,这些问题传统上是通过水平集来解决的(Boykov和Kolmogorov 2003;Kolmogorov和Boykov 2005)。
基于图切割的分割技术的最新发展包括添加连通性先验以强制前景处于一个整体(Vicente、Kol- mogorov和Rother 2008),以及添加形状先验以在分割过程中利用对象形状的知识(Lempitsky和Boykov 2007;Lempitsky、Blake和Rother 2008)。
虽然优化二进制MRF能量(4.50)需要使用组合优化技术,如最大流,但可以通过将二进制能量项转换为定义在连续[0;1]随机场上的二次能量项来获得近似解,这随后成为一个基于经典膜的正则化问题(4.24–4.27)。所得的二次能量函数可以使用标准线性系统求解器(4.27–4.28)求解,但如果速度是关键因素,则应使用多重网格或一种
(附录A.5)的变体。一旦计算出连续解,就可以在0.5处进行阈值处理,从而得到二进制分割。
[0;1]连续优化问题也可以解释为计算每个像素处随机行走者最终到达标记种子像素的概率,这等同于在电阻网格中计算势能,其中电阻等于边权重(Grady2006;Sinop和Grady2007)。K轴分割也可以通过迭代种子标签来计算,使用一个二进制问题,其中一个标签设置为1,其余所有标签设置为0,以计算每个像素的相对隶属概率。后续工作中,Grady和Ali(2008)利用线性系统特征向量的预计算,使得基于一组新颖种子的解决方案更快,这与第10.4.3节中提出的拉普拉斯遮罩问题有关(Levin,Acha,和Lischinski2008)。Couprie、Grady等人(2009)将随机行走者与分水岭和其他分割技术联系起来。Singaraju、Grady和Vidal(2008)增加了有向边约束,以支持通量,从而使能量部分呈分段二次,因此无法作为单个线性系统求解。随机行走者算法还可以用于解决Mumford-Shah分割问题(Grady和Alvino2008),并计算快速多网格解(Grady2008)。Singaraju、Grady等人(2011)对这些技术进行了很好的综述。
一种更快的方法是计算0和1种子区域之间的加权测地距离(Bai和Sapiro 2009),这种方法也可以用于估计软阿尔法遮罩(第10.4.3节)。克里米尼西、夏普和布雷克(2008)提出的一种相关方法可用于快速找到一般二值马尔可夫随机场优化问题的近似解。
散点数据插值和逼近技术是应用数学多个分支的基础。一些优秀的入门书籍和文章包括阿米德罗(2002)、温德兰(2004)和安吉奥、刘易斯和皮金(2014)。这些技术还与计算机图形学中的几何建模技术密切相关,后者仍然是一个非常活跃的研究领域。法林(2002)提供了一篇关于曲线和曲面基本样条技术的精彩介绍,而彼得斯和赖夫(2008)则涵盖了使用细分曲面的更近期方法。
数据插值和近似也是回归技术的核心,它们构成了我们在下一章学习的大多数机器学习技术的数学基础。你可以找到关于这个主题的良好介绍(以及欠拟合、过拟合、
以及经典机器学习(Bishop2006;Hastie,Tibshirani和Friedman2009;Murphy2012;Deisenroth,Faisal和Ong2020)和深度学习(Goodfellow,Bengio和Courville 2016;Glassner 2018;Zhang,Lipton等人2021)中的模型选择)。
稳健的数据拟合也是大多数计算机视觉问题的核心。虽然在本章中有所介绍,但在附录B.3中也有回顾。关于稳健拟合和统计的经典教科书和文章包括Huber(1981)、Hampel、Ronchetti等人(1986)、Black和Rangarajan(1996)、Rousseeuw和Leroy(1987)以及Stewart(1999)。Barron(2019)的最新论文统一了许多常用的稳健势函数,并展示了它们如何在机器学习应用中使用。
计算机视觉问题的正则化方法最初由Poggio、Torre和Koch(1985)以及Terzopoulos(1986a,b,1988)引入视觉领域,至今仍是解决低级视觉问题的流行框架(Ju、Black和Jepson 1996;Nielsen、Florack和Deriche 1997;Nordstrom 1990;Brox、Bruhn等人2004;Levin、Lischinski和Weiss 2008)。更详细的数学处理和更多应用可以在应用数学和统计学文献中找到(Tikhonov和Arsenin 1977;Engl、Hanke和Neubauer 1996)。
变分公式在低级计算机视觉任务中得到了广泛应用,包括光流(Horn和Schunck 1981;Nagle和Enkelmann 1986;Black和Anandan 1993;Alvarez、Weickert和Snchez 2000;Brox、Bruhn等2004;Zach、Pock和Bischof 2007a;Wedel、Cremers等2009;Werpberger、Pock和Bischof 2010)、分割(Kass、Witkin和Terzopoulos 1988;Mumford和Shah 1989;Caselles、Kimmel和Sapiro 1997;Paragios和Deriche 2000;Chan和Vese 2001;Osher和Paragios 2003;Cremers 2007)、去噪(Rudin、Osher和Fatemi 1992)、立体(Pock、Schoenemann等2008)、多视图立体(Faugeras和Keriven 1998;Yezzi和Soatto 2003;Pons、Keriven和Faugeras 2007;Labatut、Pons和Keriven 2007;Kolev、Klodt等2009)和场景流(Wedel、Brox等2011)。
关于马尔可夫随机场的文献浩如烟海,其中许多与优化和控制理论相关的出版物,视觉从业者甚至很少了解。一本很好的技术指南是布莱克、科利和罗瑟(2011)编辑的书。其他包含良好文献综述或实验比较的文章包括博伊科夫和芬卡-莱亚(2006)、泽利斯基、扎比等人(2008)、库马尔、维克斯勒和托尔(2011)以及卡佩斯、安德烈斯等人(2015)。马尔可夫随机场只是图形模型这一更广泛主题的一个版本,该主题在多本教科书和综述中有所涉及,包括毕晓普(2006,第8章)、科勒和弗里德曼(2009)、诺沃津和兰珀特(2011)以及墨菲(2012,第10、17、19章)。
关于马尔可夫随机场的开创性论文是Geman和Geman(1984)的工作,
谁将这一形式主义介绍给计算机视觉研究者,并引入了线过程的概念,即额外的二进制变量用于控制是否施加平滑惩罚。Black和Rangarajan(1996)展示了如何用稳健的成对势函数替代独立的线过程;Boykov、Veksler和Zabih(2001)开发了迭代二进制图割算法以优化多标签马尔可夫随机场;Kolmogorov和Zabih(2004)描述了这些技术所需的一类二进制能量势函数;Freeman、Pasztor和Carmichael(2000)推广了循环信念传播在MRF推理中的应用。更多参考文献可在第4.3节和4.3.2节以及附录B.5中找到。
基于连续能量(变分)的交互式分割方法包括Leclerc(1989)、Mumford和Shah(1989)、Chan和Vese(2001)、Zhu和Yuille(1996)和Tabb
以及Ahuja(1997)。这类问题的离散变体通常使用二进制图割或其他组合能量最小化方法进行优化(Boykov和Jolly 2001;Boykov和Kolmogorov 2003;Rother、Kolmogorov和Blake 2004;Kolmogorov和Boykov 2005;Cui、Yang等人2008;Vicente、Kolmogorov和Rother 2008;Lempitsky和Boykov 2007;Lempitsky、Blake和Rother 2008),尽管也可以使用连续优化技术后接阈值处理(Grady 2006;Grady和Ali 2008;Singaraju、Grady和Vidal 2008;Criminisi、Sharp和Blake 2008;Grady 2008;Bai和Sapiro 2009;Couprie、Grady等人2009)。Boykov和Funka-Lea(2006)对基于能量的各种二值对象分割技术进行了很好的综述。
例4.1:数据拟合(散点数据插值)。从一个平滑变化的函数中生成一些随机样本,然后实现并评估一种或多种数据插值技术。
1.通过将少量随机振幅和频率或尺度的正弦波或高斯函数相加,生成“随机”一维或二维函数。
2.在几十个随机位置测试此函数。
3.使用第4.1节中描述的一个或多个散点数据插值技术,将函数拟合到这些数据点。
4.在一组设定的位置上测量估计函数和原始函数之间的拟合误差,例如,在规则网格或不同的随机点上。
5.手动调整拟合算法可能需要的任何参数,以最小化输出样本拟合误差,或使用交叉验证等自动化技术。
6.用一组新的随机输入样本和输出样本位置重复此练习。最优参数是否发生变化,如果变化,变化了多少?
7.(可选)使用图像不同部分的不同随机参数生成分段平滑测试函数。数据拟合问题会变得多困难?您能想到缓解这种情况的方法吗?
尝试仅使用数组操作在NumPy(或Matlab)中实现你的算法,以便更熟悉数据并行编程和这些系统内置的线性代数运算符。使用图4.3-4.6中的数据可视化技术来调试你的算法并展示结果。
例4.2:图形模型优化。从OpenGM2库和基准测试网站http://hciweb2.iwr.uni-heidelberg.de/opengm下载并测试软件(Kappes,An-
dres等人(2015))。尝试将这些算法应用到你自己的问题上(分割、去噪等)。哪些算法更适合哪些问题?与我们在下一章研究的基于深度学习的方法相比,质量如何?
例4.3:图像去块——具有挑战性。现在你已经掌握了一些有效的方法来区分信号和噪声,开发一种技术以去除在高压缩设置下JPEG图像中出现的块状伪影(第2.3.3节)。你的方法可以简单到寻找块边界上的意外边缘,或者将量化步骤视为变换系数空间中凸区域到相应量化值的投影。
1.JPEG标头信息中提供的压缩系数知识是否有助于您更好地执行解块?请参阅Ehrlich、Lim等人(2020)关于此主题的最新论文。
2.因为量化发生在DCT变换后的YCbCr空间(2.116),在这种空间中进行分析可能更为合适。另一方面,图像先验在RGB空间中更有意义(或者不是吗?)。决定你将如何处理这一二元性,并讨论你的选择。
3.在进行此操作时,由于YCbCr转换之后是色度子采样阶段(在DCT之前),请查看是否可以使用本章讨论的较好的恢复技术之一来恢复一些丢失的高频色度信号。
4.如果你的相机有RAW + JPEG模式,你能接近无噪点的真实像素值吗?(这个建议可能没有那么有用,因为相机通常会使用相对高质量的设置来处理其RAW + JPEG模型。)
例4.4:去模糊中的推理——具有挑战性。写出图4.15中对应于非盲图像去模糊问题的图形模型,即在该问题中,模糊核事先已知。
你能想到什么样的高效的推理(优化)算法来解决这类问题?

























 654
654

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








