神经常微分方程——理解篇

1 常微分方程

常微分方程只包含单个自变量$t$，未知函数$y(t)$和未知函数的导数$y^{\prime }(t)$的等式，例如：$y^{\prime }(t)=2t$。可以写成如下通用的形式：

$$y(0)=y_0;\frac{dy}{dt}(t)=f_{\theta }(t,y(t))\text{\hspace{1em}(1)}$$

其中，$f_{\theta }(t,y(t))$表示由$t$与$y(t)$组成的某个函数，函数的常数为参数$\theta$。

求解常微分方程的方式有两种：

1）求出解析解，得到$y(t)$的具体形式，例如：$y^{\prime }(t)=2t$的通解为$y(t)=t^2+C$,$C$由$y(0)=y_0$代入确定；

2）求出数值解，例如：欧拉法,迭代求解出$y(t)$在某$t$位置的函数值，其核心思想是用切线逐步逼近求解函数：
$$y_{n+1}=y_n+f_{\theta }(t_n,y_n)(t_{n+1}-t_n)\text{\hspace{1em}(2)}$$

对于实际问题，大部分情况下都无法得到解析解。因此，求出数值解就成了唯一可行的方式。如下面示意图所示，在知道常微分方程的形式（公式(1)），我们便可以$(t_0,y_0)\to (t_1,y_1)\to ...$迭代的出解出目标位置处的解析解。

2 从残差网络到常微分方程

一层残差网络可形式化为下图：

我们可以将上面的残差网络表式成以下方程：

$$h_{t+1}=h_t+f_{\theta }(h_t)\text{\hspace{1em}(3)}$$

重新变化式(2)与式（3）得：

常微分离散化形式：$\frac{y_{n+1}-y_n}{t_{n+1}-t_n}=f_{\theta }(t_n,y_n)$
残差网络形式：$\frac{h_{t+1}-h_t}{1}=f_{\theta }(h_t)$

可知残差网络是状态步长为1，且不显式地包含自变量$t$的常微分方程。要使得残差网络能表示更一般的常微分方程，可以设计如下的网络结构（主要在输入增加变量t）：

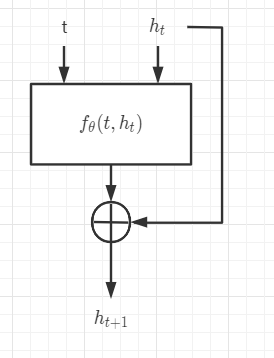
从上可以分析得出，残差网络（本质上和欧拉法一样）可用来计算常微分方程的数值解。通过给$f_{\theta }(t,h_t)$乘上可变的步长$dt$，便得到更加一般的形式：
$h_{t+1}=h_t+f_{\theta }(t,h_t)dt$

但是，用欧拉法与残差网络来计算常微分方程的数值解太过粗糙。如果用一个抽象的概念来代替欧拉法与残差网络，例如ODESolver网络，其中ODESolver是一个函数，它提供了ODE的解决方法，其精度比欧拉法高得多。这就是神经常微分方程（把ODESolver当成一个黑盒）：

3 怎么训练神经常微分方程

在算法 1 ¹中，陈天琦等研究者展示了如何借助另一个 OED Solver 一次性求出反向传播的各种梯度和更新量。要理解算法 1，首先我们要熟悉 ODESolver 的表达方式。例如在 ODEnet 的前向传播中，求解过程可以表示为 ODEsolver(z(t_0), f, t_0, t_1, θ)，我们可以理解为从 t_0 时刻开始令 z(t_0) 以变化率 f 进行演化，这种演化即 f 在 t 上的积分，ODESolver 的目标是通过积分求得 z(t_1)。

同样我们能以这种方式理解算法 1，我们的目的是利用 ODESolver 从 z(t_1) 求出 z(t_0)、从 a(t_1) 按照方程 4 积出 a(t_0)、从 0 按照方程 5 积出 dL/dθ。最后我们只需要使用 dL/dθ 更新神经网络 f(z(t), t, θ) 就完成了整个反向传播过程。

4. 伴随法BP的推导

动态微分系统的数据集中的元素可以由<时间，状态>对表示，标记为$(z,t)$。

假定我们要学习的动态微分系统的形式为：
$$\frac{dz}{dt}=f(z(t),t)\text{\hspace{1em}(4)}$$
用于学习的观测数据集为$\{(z_0,t_0),(z_1,t_1),...,(z_N,t_N)\}$。

我们利用可学习的网络模型$\hat{f}(z,t,\theta )$来近似动态系统真实的微分函数$f(z,t)$。

若以某状态$z_0$为起始状态（假定$z_0$在数据集中的时间标记为$t_0$），我们验证所学到的网络模型是否很好的近似了真实的微分函数$f(z,t)$的基本方式为：

• 以$z_0$作为起始状态，以网络模型作为微分函数，利用ODE Solver求得$t_1$时刻的状态${\hat{z}}_1$；
• 从数据集中找到时间标记为$t_1$的状态$z_1$；
• 利用${\hat{z}}_1$与$z_1$的差异来度量学习效果，一种可能的损失函数为$L({\hat{z}}_1)=\frac{1}{2}||{\hat{z}}_1-z_1|{|}_2^2$。

实际数据不可能只有一个样本，那么损失函数的一般形式采用如下所示的均方误差（MSE）：

$$L=\frac{1}{N}\sum _{i=1}^N||{\hat{z}}_i-z_i|{|}_2^2=\frac{1}{N}\sum _{i=1}^N||{\int }_{t_{i-1}}^{t_i}\hat{f}(z,t,\theta )dt-z_i|{|}_2^2=\frac{1}{N}\sum _{i=1}^N||ODESolver(z_{i-1},f,t_{i-1},t_i,\theta )-z_i|{|}_2^2\text{\hspace{1em}(5)}$$

我们要更新的模型参数为$\theta$，因此，我们最终需要得到的是$\frac{dL}{d\theta }$。但是，从$z(t_{i-1})$到$z(t_i)$利用了ODESolver算子，一个python版本的ODESolver算子如下所示：

def ode_solve(z0, t0, t1, f):
    """
    Simplest Euler ODE initial value solver
    """
    h_max = 0.05
    n_steps = math.ceil((abs(t1 - t0)/h_max).max().item())

    h = (t1 - t0)/n_steps
    t = t0
    z = z0

    for i_step in range(n_steps):
        z = z + h * f(z, t)
        t = t + h
    return z

当系统是时变的，输入$t$是作为网络的输入，当系统是时不变的，$t$在此处对函数的输出没有影响。一个时不变的$f$例子给出如下：

class LinearODEF(ODEF):
    def __init__(self, W):
        super(LinearODEF, self).__init__()
        self.lin = nn.Linear(2, 2, bias=False)
        self.lin.weight = nn.Parameter(W)

    def forward(self, x, t):
        return self.lin(x)

虽然，构建的网络模型基于函数$f$，但是完整的网络是基$f$与ODESolver，并采用一个设定时间步$dt$的累积函数${\hat{\mathbf{z}}}_n=Net({\mathbf{z}}_0,\theta ,t_0,t_1)={\mathbf{z}}_0+{\sum }_{i=1}^{n}f({\hat{\mathbf{z}}}_{i-1},t_{i-1},\theta )dt$，其中，$n=\frac{t_1-t_0}{dt}$。为了得到$\frac{dL}{d\theta }$，我们需要采用与反向传播算法一样的链式法则，同时需要计算$\frac{dL}{d\hat{\mathbf{z}}},\frac{dL}{dt}$。

令$\mathbf{a}(t)=\frac{dL}{d\hat{\mathbf{z}}(t)}$，我们有:
$$\frac{d\mathbf{a}(t)}{dt}=-\mathbf{a}(t)\frac{\partial f(\mathbf{z}(t),t,\theta )}{\partial \mathbf{z}(t)}\text{\hspace{1em}(6)}$$

式(6)的证明：

其中第二行中分子的第二项证明（上面第三行为泰勒展开）：
$\mathbf{z}(t+ϵ)={\int }_t^{t+ϵ}f(\mathbf{z}(t),t,\theta )dt+\mathbf{z}(t)=T_{ϵ}(\mathbf{z}(t),t)$
$\frac{dL}{\partial \mathbf{z}(t)}=\frac{dL}{d\mathbf{z}(t+ϵ)}\frac{d\mathbf{t}+ϵ}{d\mathbf{z}(t)}\Rightarrow \mathbf{a}(t)=\mathbf{a}(t+ϵ)\frac{\partial T_{ϵ}(\mathbf{z}(t),t)}{\partial \mathbf{z}(t)}$

假如，我们从$\{({\mathbf{z}}_0,t_0),({\mathbf{z}}_1,t_1),...,({\mathbf{z}}_N,t_N)\}$中抽取一个样本$({\mathbf{z}}_{N-1},t_{N-1})\to ({\mathbf{z}}_N,t_N)$，表示以${\mathbf{z}}_{N-1}$为起始状态，经过时间$t_N-t_{N-1}$，动态系统（此处假设为时不变系统）的状态变为${\mathbf{z}}_N$。由内嵌ODESolver算子的神经网络模型得到的状态为${\hat{\mathbf{z}}}_N$。

由于${\hat{\mathbf{z}}}_N$相当于一般学习任务的输出$y$，所以$\frac{dL}{d\hat{\mathbf{z}}(t_N)}=\frac{d}{d{\hat{\mathbf{z}}}_N}(\frac{1}{2}||{\hat{\mathbf{z}}}_N-{\mathbf{z}}_N|{|}_2^2)$，直接能得到结果。

重要的是怎么得到$\frac{dL}{{\hat{\mathbf{z}}}_{N-1}}$（从${\hat{\mathbf{z}}}_{N-1}$到${\hat{\mathbf{z}}}_N$的过程是一个多次累积的ODESolver算法），根据公式(6)有：
$$\frac{dL}{d{\hat{\mathbf{z}}}_{N-1}}=\mathbf{a}(t_{N-1})=\mathbf{a}(t_N)+{\int }_{t_N}^{t_{N-1}}\frac{d\mathbf{a}(t)}{dt}dt=\mathbf{a}(t_N)-{\int }_{t_N}^{t_{N-1}}\mathbf{a}(t{)}^T\frac{\partial f(\hat{\mathbf{z}}(t),t,\theta )}{\partial \hat{\mathbf{z}}(t)}\text{\hspace{1em}(7)}$$

我们可以看到，公式(7)用ODESolver算法就将梯度$\frac{dL}{d{\hat{\mathbf{z}}}_N}$反向传播给$\frac{dL}{d{\hat{\mathbf{z}}}_{N-1}}$。

如下图所示，数据是按$t_0\to t_1$,$t_1\to t_2$,…,$t_{N-1}\to t_N$组合作为训练数据的，但是$\frac{dL}{d\hat{\mathbf{z}}(t_N)}$的梯度可以传播给$t_{N-1}$，也可以继续往后传播给$t_{N-2}$直至数据采集时的起点$t_0$。所有前方的数据都可以把梯度传播给它后方（下图右²为前，左为后）用于训练。

不要忘记了我们的目的，计算$\frac{dL}{d\theta }$。
ODESolver算子以${\hat{\mathbf{z}}}_i$作为中间状态，我们根据链式法则有${\mathbf{a}}_{\theta }(t)=\frac{dL}{d\theta }=\frac{dL}{d\hat{\mathbf{z}}}\frac{d\hat{\mathbf{z}}}{d\theta }=\mathbf{a}(t)\frac{d\hat{\mathbf{z}}}{d\theta }$

我们可以先求得$\frac{dL}{d\theta }=\int \frac{d}{dt}\frac{dL}{d\theta }dt$中的$\frac{d}{dt}\frac{dL}{d\theta }$。
$\frac{d}{dt}\frac{dL}{d\theta }=\frac{d}{d\theta }\frac{dL}{d\hat{\mathbf{z}}}\frac{d\hat{\mathbf{z}}}{dt}=\frac{d}{d\theta }\mathbf{a}(t)f(\hat{\mathbf{z}},t,\theta )=\mathbf{a}(t)\frac{\partial f(\hat{\mathbf{z}},t,\theta )}{\partial \theta }$
将${\mathbf{a}}_{\theta }(t_N)=0$，得：

$${\mathbf{a}}_{\theta }(t_{N-1})=\frac{dL}{d\theta }=-{\int }_{t_N}^{t_{N-1}}\mathbf{a}(t)\frac{\partial f(\hat{\mathbf{z}},t,\theta )}{\partial \theta }dt\text{\hspace{1em}(8)}$$

当然，还需要求（对于时变系统需要）${\mathbf{a}}_t(t)=\frac{dL}{dt}=\frac{dL}{d\hat{\mathbf{z}}}\frac{d\hat{\mathbf{z}}}{dt}=\mathbf{a}(t)f(\hat{\mathbf{z}},t,\theta )$，由于我们想求任意时刻的${\mathbf{a}}_t(t)$,而网络模型的forward只输出$t_N$时刻的$f(\widehat{{\mathbf{z}}_N},t_N,\theta )$，依据此式，我们只能计算出${\mathbf{a}}_t(t_N)=\mathbf{a}(t_N)f(\widehat{{\mathbf{z}}_N},t_N,\theta )$。，因此需要寻找其它计算形式：
我们可以令$\frac{dL}{dt}=\int \frac{d}{dt}\frac{dL}{dt}dt,$
$\frac{d}{dt}\frac{dL}{dt}=\frac{d}{dt}\frac{dL}{d\hat{\mathbf{z}}}\frac{d\hat{\mathbf{z}}}{dt}=\mathbf{a}(t)\frac{\partial f(\hat{\mathbf{z}},t,\theta )}{\partial t}$
根据上面我们有${\mathbf{a}}_t(t_N)=\mathbf{a}(t_N)f(\widehat{{\mathbf{z}}_N},t_N,\theta )$
则可得：
$${\mathbf{a}}_t(t_{N-1})=\frac{dL}{d{t}_{N-1}}={\mathbf{a}}_t(t_N)-{\int }_{t_N}^{t_{N-1}}\mathbf{a}(t)\frac{\partial f(\hat{\mathbf{z}}(t),t,\theta )}{\partial t}dt\text{\hspace{1em}(9)}$$

参考

---

1. Chen R, Rubanova Y, Bettencourt J and Duvenaud D. Neural Ordinary Differential Equations(PDF). NeurIPS 2018. ↩︎

2. Neural Ordinary Differential Equations(Jupyter notebook). ↩︎