陈省身 | 从三角形到流形

注：英文引文，机翻未校。

---

From Triangles to Manifolds

从三角形到流形

The American Mathematical Monthly, Vol. 86, No. 5. (May, 1979), pp. 339 - 349.
《美国数学月刊》，第 86 卷，第 5 期（1979 年 5 月），第 339 - 349 页。

1.Geometry.

几何学

I believe I am expected to tell you all about geometry; what it is, its developments through the centuries, its current issues and problems, and, if possible, a peep into the future. The first question does not have a clear - cut answer. The meaning of the word geometry changes with time and with the speaker. With Euclid, geometry consists of the logical conclusions drawn from a set of axioms. This is clearly not sufficient with the horizons of geometry ever widening. Thus in 1932 the great geometers O. Veblen and J. H. C. Whitehead said, “A branch of mathematics is called geometry, because the name seems good on emotional and traditional grounds to a sufficiently large number of competent people” [1]. This opinion was enthusiastically seconded by the great French geometer Elie Cartan [2]. Being an analyst himself, the great American mathematician George Birkhoff mentioned a “disturbing secret fear that geometry may ultimately turn out to be no more than the glittering intuitional trappings of analysis” [3]. Recently my friend Andre Weil said: “The psychological aspects of true geometric intuition will perhaps never be cleared up. At one time it implied primarily the power of visualization in three - dimensional space. Now that higher - dimensional spaces have mostly driven out the more elementary problems, visualization can at best be partial or symbolic. Some degree of tactile imagination seems also to be involved” [4].

我相信大家期待我来谈谈几何学，包括它是什么、几个世纪以来的发展、当前的问题和挑战，如果可能的话，还可以展望一下未来。然而，第一个问题并没有明确的答案。几何学的含义随着时间的推移和不同人的理解而发生变化。在欧几里得时代，几何学是从一组公理中推导出的逻辑结论。然而，随着几何学的不断发展，这种定义显然已经不够用了。1932 年，伟大的几何学家 O. Veblen 和 J. H. C. Whitehead 说过：“一个数学分支被称为几何学，是因为这个名字在情感和传统上得到了足够多有能力的人的认可” [1]。这一观点得到了法国著名几何学家 Elie Cartan 的热烈支持 [2]。作为一位分析学家，美国著名数学家 George Birkhoff 曾提到过一种“令人不安的秘密恐惧，即几何学最终可能只是分析学的闪闪发光的直觉外衣” [3]。我的朋友 Andre Weil 最近也说过：“真正的几何直觉的心理方面或许永远不会被完全弄清楚。曾经，它主要意味着在三维空间中的可视化能力。然而，随着高维空间的研究逐渐取代了更基础的问题，可视化最多只能是部分的或象征性的。似乎还涉及一定程度的触觉想象力” [4]。

At this point it is perhaps better to let things stand and turn to some concrete topics.
或许在这一点上，我们最好暂时搁置这些讨论，转向一些具体的话题。

2.Triangles.

三角形

Among the simplest geometrical figures is the triangle, which has many beautiful properties. For example, it has one and only one inscribed circle and also one and only one circumscribed circle. At the beginning of this century the nine - point circle theorem was known to almost every educated mathematician. But its most intriguing property concerns the sum of its angles. Euclid says that it is equal to 180°, or $\pi$ by radian measure, and deduces this from a sophisticated axiom, the so - called parallel axiom. Efforts to avoid this axiom failed. The result was the discovery of non - Euclidean geometries in which the sum of angles of a triangle is less or greater than $\pi$, according as the geometry is hyperbolic or elliptic. The discovery of hyperbolic non - Euclidean geometry, in the eighteenth century by Gauss, John Bolyai, and Lobatchevsky, was one of the most brilliant chapters in human intellectual history.

在最简单的几何图形中，三角形具有许多优美的性质。例如，它有且仅有一个内切圆和一个外接圆。在本世纪初，九点圆定理几乎为每一位受过教育的数学家所熟知。然而，三角形最引人入胜的性质是其内角和。欧几里得认为三角形的内角和等于 180°，或用弧度制表示为 $\pi$，这一结论是基于一个复杂的公理——平行公理推导出来的。然而，试图避开这一公理的努力都失败了。结果就是发现了非欧几里得几何，在这种几何中，三角形的内角和小于或大于 $\pi$，具体取决于它是双曲几何还是椭圆几何。18 世纪，高斯、约翰·波尔约和罗巴切夫斯基发现了双曲非欧几里得几何，这是人类思想史上最为辉煌的篇章之一。

The generalization of a triangle is an $n$-gon, a polygon with n sides. By cutting the $n$-gon into $n-2$ triangles, one sees that the sum of its angles is $(n-2)\pi$. It is better to measure the sum of the exterior angles! The latter is equal to $2\pi$, for all $n$-gons, including triangles.
三角形的推广是 $n$ 边形，即有 $n$ 条边的多边形。将 $n$ 边形切割成 $n-2$ 个三角形，可以看出其内角和为 $(n-2)\pi$。其实，测量外角和会更好！对于所有 $n$ 边形，包括三角形，其外角和都等于 $2\pi$。

3.Curves in the plane; rotation index and regular homotopy.

平面曲线；旋转指数和正则同伦

By applying calculus we can consider smooth curves and closed smooth curves in the plane, i.e, curves with a tangent line everywhere and varying continuously. As a point moves along a closed smooth (oriented) curve C once, the lines through a fixed point O and parallel to the tangent lines of C rotate through an angle $2n\pi$ or rotate n times about O. This integer $n$ is called the rotation index of C. (See Fig. 1.)

通过应用微积分，我们可以考虑平面上的光滑曲线和闭合光滑曲线，即处处有切线且连续变化的曲线。当一个点沿着一条闭合光滑（定向）曲线 C 移动一次时，通过一个固定点 O 且与 C 的切线平行的直线会旋转一个角度 $2n\pi$，或者围绕 O 点旋转 $n$ 次。这个整数 $n$ 被称为曲线 C 的旋转指数。（见图 1）

A famous theorem in differential geometry says that if C is a simple curve, i.e., if C does not intersect itself, $n=\pm 1$.

微分几何中有一个著名的定理，如果 C 是一条简单曲线，即 C 不与自身相交，那么 $n=\pm 1$。

Clearly, there should be a theorem combining the theorem on the sum of exterior angles of an $n$-gon and the rotation index theorem of a simple closed smooth curve. This is achieved by considering the wider class of simple closed sectionally smooth curves. The rotation index of such a curve can be defined in a natural way by turning the tangent at a corner an amount equal to the exterior angle. (See Fig. 2.) Then the rotation index theorem above remains valid for simple closed sectionally smooth curves. In the particular case of an n - gon formed by straight segments, this reduces to the statement that the sum of its exterior angles is $2\pi$.

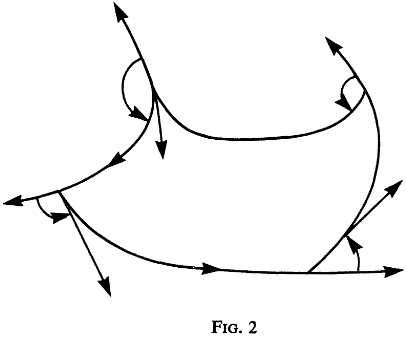
显然，应该有一个定理将 $n$ 边形的外角和定理与简单闭合光滑曲线的旋转指数定理结合起来。通过考虑更广泛的简单闭合分段光滑曲线类来实现这一点。通过将拐角处的切线转动一个等于外角的量，可以自然地定义这种曲线的旋转指数。（见图 2）然后上述旋转指数定理对于简单闭合分段光滑曲线仍然有效。在由直线段构成的 n 边形的特殊情况下，这简化为它的外角和是 $2\pi$ 的陈述。

This theorem can be further generalized. Instead of simple closed curves we can allow closed curves to intersect themselves. A generic self-intersection can be assigned a sign. Then, if the curve is properly oriented, the rotation index is equal to one plus the algebraic sum of the number of self - intersections. (See Fig. 3.) For example, the figure 8 has the rotation index zero.

这个定理可以进一步推广。我们不仅可以考虑简单闭合曲线，还可以允许闭合曲线自身相交。一个普通的自交点可以被赋予一个符号。然后，如果曲线被正确地定向，旋转指数等于一加上自交点数的代数和。（见图 3）例如，数字 8 的形状的旋转指数为零。

A fundamental notion in geometry, or in mathematics in general, is deformation or homotopy. Two closed smooth curves are said to be regularly homotopic if one can be deformed to the other through a family of closed smooth curves. Since the rotation index is an integer and varies continuously in the family, it must remain a constant; i.e., it keeps the same value when the curve is regularly deformed. A remarkable theorem of Graustein - Whitney says that the converse is true [5]: Two closed smooth curves with the same rotation index are regularly homotopic.

在几何学中，或者在数学中，一个基本的概念是变形或同伦。如果一条闭合光滑曲线可以通过一族闭合光滑曲线变形为另一条曲线，则称这两条闭合光滑曲线是正则同伦的。由于旋转指数是一个整数，并且在这一族曲线中连续变化，因此它必须保持不变；即，当曲线被正则变形时，它保持相同的值。Graustein - Whitney 的一个杰出定理表明，逆命题也是成立的 [5]：具有相同旋转指数的两条闭合光滑曲线是正则同伦的。

It is a standard practice in mathematics that in order to study closed smooth curves in the plane it is more profitable to look at all curves and to put them into classes, the regular homotopy classes in this case being an example. This may be one of the essential methodological differences between theoretical science and experimental science, where such a procedure is impractical. The Graustein - Whitney theorem says that the only invariant of a regular homotopy class is the rotation index.
在数学中，为了研究平面上的闭合光滑曲线，更有利的做法是观察所有曲线并将它们分类，正则同伦类就是一个例子。这可能是理论科学与实验科学之间的一个基本方法论差异，在实验科学中，这种程序是不切实际的。Graustein - Whitney 定理表明，正则同伦类的唯一不变量是旋转指数。

4.Euclidean three - space.

欧几里得三维空间

From the plane we pass to the three - dimensional Euclidean space where the geometry is richer and has distinct features. Perhaps the nicest space curve which does not lie in a plane is a circular helix. It has constant curvature and constant torsion and is the only curve admitting co’ rigid motions. There is an essential difference between right - handed and left - handed helices (See Fig. 4), depending on the sign of the torsion; a right - handed helix cannot be congruent to a left - handed one, except by a mirror reflection.

从平面过渡到三维欧几里得空间，这里的几何学更加丰富，具有独特的特征。或许最优美的一条不位于平面上的空间曲线是圆柱螺旋线。它具有恒定的曲率和恒定的挠率，并且是唯一允许刚性运动的曲线。右旋螺旋线和左旋螺旋线之间存在本质区别（见图 4），这取决于挠率的符号；右旋螺旋线不能与左旋螺旋线全等，除非通过镜像反射。

Helices play an important role in mechanics. From a geometrical viewpoint it may not be an entire coincidence that the Crick - Watson model of a DNA - molecule is double - helical. A double helix has interesting geometrical properties. In particular, by joining the end points of the helices by segments or arcs, we get two closed curves. In three - dimensional space they have a linking number. (See Fig. 5.)

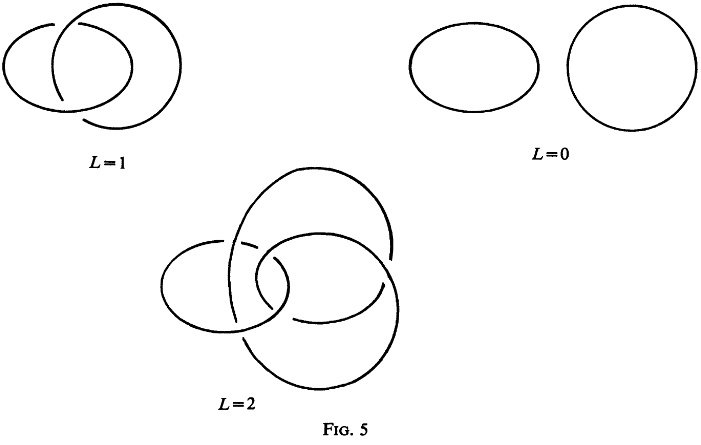
螺旋线在力学中扮演着重要角色。从几何学的角度来看，克里克 - 沃森的 DNA 分子模型是双螺旋结构，这或许并非完全巧合。双螺旋具有有趣的几何性质。特别是，通过用线段或弧连接螺旋线的端点，我们得到两条闭合曲线。在三维空间中，它们具有一个环绕数。（见图 5）

A recent controversial issue in biochemistry, raised by the mathematicians William Pohl and George Roberts, is whether the chromosomal DNA is double - helical. In fact, if it is, it will have two closed strands with a linking number of the order of 300,000. The molecule is replicated by separation of the strands and formation of the complementary strand of each. With such a large linking number Pohl and Roberts showed that the replication process would have severe mathematical difficulties. Thus the double - helical structure of the DNA molecule, at least for the chromosome, has been questioned [6]. (Added January 26, 1979: A number of recent experiments have shown that some of the mathematical difficulties for the double helical structure of the DNA - molecule can be overcome by enzymatic activities (cf. F. H. C. Crick, Is DNA really a double helix? preprint, 1978).)

生物化学中最近的一个有争议的问题是由数学家 William Pohl 和 George Roberts 提出的，即染色体 DNA 是否是双螺旋结构。事实上，如果是的话，它将有两个闭合的链，其环绕数约为 300,000。该分子通过分离链并形成每条链的互补链来复制。鉴于如此大的环绕数，Pohl 和 Roberts 指出，复制过程将面临严重的数学困难。因此，至少对于染色体而言，DNA 分子的双螺旋结构受到了质疑 [6]。（1979 年 1 月 26 日补充：最近的一些实验表明，DNA 分子的双螺旋结构的一些数学困难可以通过酶的活性来克服（参见 F. H. C. Crick，《DNA 真的是双螺旋吗？》预印本，1978 年）。）

The linking number $L$ is determined by the formula of James H. White [7]:
环绕数 $L$ 由 James H. White 的公式 [7] 确定：

$$T+W=L,\text{\hspace{1em}(1)}$$

where $T$ is the total twist and $W$ the writhing number. The latter can be experimentally measured and changes by the action of an enzyme. This formula is of fundamental importance in molecular biology. Generally DNA molecules are long. In order to store them in limited space, the most economical way is to writhe and coil them. These discussions could indicate the beginning of a stochastic geometry, with the main examples drawn from biology.
其中 $T$ 是总扭曲数，$W$ 是缠结数。后者可以通过实验测量，并且会因酶的作用而改变。这个公式在分子生物学中具有根本性的重要性。一般来说，DNA 分子很长。为了在有限的空间内储存它们，最经济的方法是使它们扭曲和盘绕。这些讨论可能标志着随机几何学的开端，其主要例子来自生物学。

In a three - dimensional space surfaces have far more important properties than curves.Gauss’s fundamental work elevated differential geometry from a chapter of calculus to an independent discipline. His Disquisitiones generales circa superficies curvas (1827) is the birth certificate of differential geometry. The main idea is that a surface has an intrinsic geometry based on the measure of arc length alone. From the element of arc other geometric notions, such as the angle between curves and the area of a piece of surface, can be defined. Plane geometry is thus generalized to any surface based only on the local properties of the element of arc. This localization of geometry is both original and revolutionary. In place of the straight lines are the geodesics, the “shortest” curves between any two points (sufficiently close). More generally, a curve on $\Sigma$ has a “geodesic curvature” generalizing the curvature of a plane curve and geodesics are the curves whose geodesic curvature vanishes identically.
在三维空间中，曲面的性质远比曲线更为重要。高斯的开创性工作将微分几何从微积分的一个章节提升为一门独立的学科。他的《Disquisitiones generales circa superficies curvas》（1827）是微分几何的出生证明。其主要思想是，曲面具有一种基于弧长测量的内在几何。从弧长元素出发，可以定义其他几何概念，例如曲线之间的夹角和曲面片的面积。平面几何因此被推广到任何曲面，仅基于弧长元素的局部性质。这种几何的局部化既具有原创性，又具有革命性。直线的位置被测地线所取代，测地线是任意两点（足够接近）之间的“最短”曲线。更一般地，曲面 $\Sigma$ 上的曲线具有“测地曲率”，这是平面曲线曲率的推广，而测地线是测地曲率恒等于零的曲线。

Let the surface $\Sigma$ be smooth and oriented. At every point $p$ of $\Sigma$ there is a unit normal vector $\mathbf{v}(p)$ which is perpendicular to the tangent plane to $\Sigma$ at $p$. (See Fig. 6.) The vector $\mathbf{v}(p)$ can be viewed as a point of the unit sphere $S_0$ with center at the origin of the space. By sending $p$ to $\mathbf{v}(p)$ we get the Gauss mapping

设曲面 $\Sigma$ 是光滑且定向的。在 $\Sigma$ 的每一点 $p$ 处，存在一个单位法向量 $\mathbf{v}(p)$，它垂直于 $p$ 点处的切平面。（见图 6）向量 $\mathbf{v}(p)$ 可以被看作是以空间原点为中心的单位球面 $S_0$ 上的一个点。通过将 $p$ 映射到 $\mathbf{v}(p)$，我们得到高斯映射：

$$g:\Sigma \to S_0.\text{\hspace{1em}(2)}$$

The ratio of the element of the area of $S_0$ to the element of area of $\Sigma$ under this mapping is called the Gaussian curvature. Gauss’s “remarkable theorem” says that the Gaussian curvature depends only on the intrinsic geometry of $\Sigma$. In fact, in a sense it characterizes this geometry. Clearly the Gaussian curvature is zero if $\Sigma$ is the plane.

在这种映射下，$S_0$ 的面积元素与 $\Sigma$ 的面积元素的比值被称为高斯曲率。高斯的“卓越定理”表明，高斯曲率仅依赖于 $\Sigma$ 的内在几何。事实上，从某种意义上说，它表征了这种几何。显然，如果 $\Sigma$ 是平面，高斯曲率则为零。

As in plane geometry we consider on $\Sigma$ a domain $D$ bounded by one or more sectionally smooth curves. $D$ has an important topological invariant $\chi (D)$, called its Euler characteristic, which is most easily defined as follows: Cut $D$ into polygons in a “proper way” and denote by $v$, $e$, and $f$ the number of vertices, edges, and faces, respectively. Then

正如在平面几何中一样，我们在 $\Sigma$ 上考虑一个由一条或多条分段光滑曲线围成的区域 $D$。$D$ 有一个重要的拓扑不变量 $\chi (D)$，称为其欧拉特征数，其最简单的定义如下：以“适当的方式”将 $D$ 切割成多边形，并分别用 $v$、$e$ 和 $f$ 表示顶点数、边数和面数。那么

$$\chi (D)=v-e+f.\text{\hspace{1em}(3)}$$

(Euler’s polyhedral theorem was known before Euler, but Euler seems to have been the first one to recognize explicitly the importance of the “alternating sum.”)
（欧拉多面体定理在欧拉之前就已经被知晓，但欧拉似乎是第一个明确认识到“交替和”重要性的人。）

The Gauss - Bonnet formula in surface theory is

曲面理论中的高斯 - 博内公式为：

$$\sum \text{ext angles}+{\int }_{\partial D}\text{geod curv}+{\iint }_D\text{Gaussian curv}=2\pi \chi (D),\text{\hspace{1em}(4)}$$

where $\partial D$ is the boundary of $D$. For a plane domain the Gaussian curvature is zero. If in addition the domain is simply connected, we have $\chi (D)=1$. Then this formula reduces to the rotation index theorem discussed in §3. We are indeed a long way from the sum of angles of a triangle.
其中 $\partial D$ 是 $D$ 的边界。对于平面区域，高斯曲率为零。如果该区域是单连通的，那么 $\chi (D)=1$。此时，该公式简化为第 3 节中讨论的旋转指数定理。我们确实已经远离了三角形内角和的研究。

Generalizing the geometry of closed plane curves we can consider closed oriented surfaces in space. The generalization of the rotation index is the degree of the Gauss mapping $g$ in (2). The precise definition of the degree is sophisticated. Intuitively it is the number of times that the image $g(\Sigma )$ covers $S_0$, counted with sign. Unlike the plane, where the rotation index can be any integer, the degree $d$ is completely determined by the topology of $\Sigma$; it is equal to

将平面闭曲线的几何推广到空间中的闭合定向曲面。旋转指数的推广是高斯映射 $g$ 在（2）中的度数。度数的精确定义是复杂的。直观上，它是像 $g(\Sigma )$ 覆盖 $S_0$ 的次数，带有符号。与平面不同，平面中的旋转指数可以是任意整数，而度数 $d$ 完全由 $\Sigma$ 的拓扑决定；它等于

$$d=\frac{1}{2}\chi (\Sigma ).\text{\hspace{1em}(5)}$$

For the imbedded unit sphere this degree is $+1$ independently of its orientation. A surprising result of S. Smale [8] says that the two oppositely oriented unit spheres are indeed regularly homotopic or, more intuitively, that the unit sphere can be turned inside out through a regular homotopy. It is essential that at each stage of the homotopy the surface has a tangent plane everywhere, but is allowed to intersect itself.
对于嵌入的单位球面，这个度数为 $+1$，与其定向无关。S. Smale [8] 的一个惊人结果表明，两个方向相反的单位球面确实是正则同伦的，或者更直观地说，单位球面可以通过正则同伦翻转过来。在同伦的每个阶段，曲面处处都有切平面是至关重要的，但它允许自相交。

5.From coordinate spaces to manifolds.

从坐标空间到流形

It was Descartes who in the seventeenth century revolutionized geometry by using coordinates. Quoting Hermann Weyl, “The introduction of numbers as coordinates was an act of violence” [9]. From now on, paraphrasing Weyl, figure and number, like angel and devil, fight for the soul of every geometer. In the plane the Cartesian coordinates of a point are its distances, with signs, from two fixed perpendicular lines, the coordinate axes. A straight line is the locus of all points whose coordinates $x,y$ satisfy a linear equation

正是笛卡尔在 17 世纪通过引入坐标彻底改变了几何学。引用赫尔曼·外尔的话，“将数字引入作为坐标是一种暴力行为” [9]。从现在开始，引用外尔的话，图形和数字，就像天使和魔鬼一样，争夺每一个几何学家的灵魂。在平面上，一个点的笛卡尔坐标是其到两条固定垂直线（坐标轴）的距离，带有符号。一条直线是所有满足线性方程的点 $x,y$ 的轨迹：

$$ax+by+c=0\text{\hspace{1em}(6)}$$

The result is the translation of geometry into algebra.
其结果是将几何学转化为代数。

Once the door was opened for analytic geometry, other coordinate systems came into play. Among them are polar coordinates in the plane and spherical coordinates, cylindrical coordinates in space, and elliptic coordinates in the plane and in space. The latter are adapted to the confocal quadrics and are particularly suited to the study of the ellipsoids, which include our earth.
一旦为解析几何打开了大门，其他坐标系也随之被引入。其中包括平面上的极坐标和球坐标，空间中的柱坐标，以及平面上和空间中的椭圆坐标。后者适用于共焦二次曲面，特别适合研究椭球体，包括我们居住的地球。

There is also a need for higher dimensions. For even if we start with a three - dimensional space, the theory of relativity calls for the inclusion of time as a fourth dimension. On a more elementary level, to record the motion of a particle, including its velocity, requires six coordinates (the hodograph). All the continuous functions in one variable form an infinite - dimensional space. Those which are square - integrable form a Hilbert space, which can be coordinatized by an infinite sequence of coordinates. Such a viewpoint, of considering all functions with prescribed properties, is fundamental in mathematics.
还有对更高维度的需求。因为即使我们从三维空间开始，相对论也需要将时间作为第四维纳入其中。在更基础的层面上，记录一个粒子的运动，包括其速度，需要六个坐标（速度图）。所有单变量的连续函数构成一个无限维空间。其中平方可积的函数形成一个希尔伯特空间，可以用无限序列的坐标来表示。这种观点，即考虑所有具有特定性质的函数，在数学中是基础性的。

From the proliferation of coordinate systems it is natural to have a theory of coordinates.
从坐标系的大量涌现中，自然会产生坐标理论。

General coordinates need only the property that they can be identified with points; i.e., there is a one - to - one correspondence between points and their coordinates—their origin and meaning are inessential.
一般坐标只需要具有能够与点对应起来的性质，即点与它们的坐标之间存在一一对应关系——它们的起源和含义是不重要的。

If you find it difficult to accept general coordinates, you will be in good company. It took Einstein seven years to pass from his special relativity in 1908 to his general relativity in 1915. He explained the long delay in the following words: “why were another seven years required for the construction of the general theory of relativity? The main reason lies in the fact that it is not so easy to free oneself from the idea that coordinates must have an immediate metrical meaning” [10].
如果你觉得难以接受一般坐标，你并不孤单。爱因斯坦花了七年时间才从 1908 年的狭义相对论过渡到 1915 年的广义相对论。他用以下话语解释了这种长期的延迟：“为什么还需要另外七年时间来构建广义相对论？主要原因在于，摆脱坐标必须具有直接的度量意义这一观念并非易事” [10]。

After being served by coordinates in the study of geometry, we now wish to be free from their bond. This leads to the fundamental notion of a manifold. A manifold is described locally by coordinates, but the latter are subject to arbitrary transformations. In other words, it is a space with transient or relative coordinates (principle of relativity). I would compare the concept with the introduction of clothing to human life. It was a historical event of the utmost importance that human beings began to clothe themselves. No less significant was the ability of human beings to change their clothing. If geometry is the human body and coordinates are clothing, then the evolution of geometry has the following comparison.
在几何学研究中利用坐标之后，我们现在希望摆脱它们的束缚。这就引出了流形的基本概念。流形是通过坐标局部描述的，但这些坐标可以进行任意变换。换句话说，它是一个具有短暂或相对坐标的空间（相对性原理）。我会将这个概念与人类生活中引入服装相比较。人类开始穿衣是一个极其重要的历史事件。而人类能够更换服装的能力同样意义重大。如果几何学是人体，坐标是服装，那么几何学的发展可以进行如下类比。

Synthetic geometry 综合几何	Naked man 赤身的人
Coordinate geometry 坐标几何	Primitive man 原始人
Manifolds 流形	Modern man 现代人

A manifold is a sophisticated concept even for mathematicians. For example, a great mathematician such as Jacques Hadamard “felt insuperable difficulty… in maintaining more than a rather elementary and superficial knowledge of the theory of Lie groups” [11], a notion based on that of a manifold.
即使是数学家，流形也是一个复杂的概念。例如，像雅克·阿达马这样的伟大数学家“在保持对李群理论的较为基础和肤浅的认识方面感到难以克服的困难” [11]，而李群理论是基于流形的概念。

6.Manifolds; local tools.

流形；局部工具

With coordinates practically meaningless there is a need for new tools in studying manifolds. The key word is invariance. Invariants are of two kinds: local and global. The former refer to the behavior under a change of the local coordinates, while the latter are global invariants of the manifold, examples being the topological invariants. Two of the most important local tools are the exterior differential calculus and Ricci’s tensor analysis.
由于坐标实际上失去了意义，因此需要新的工具来研究流形。关键词是不变性。不变量分为两种：局部不变量和全局不变量。前者指的是在局部坐标变化下的行为，而后者是流形的全局不变量，例如拓扑不变量。最重要的两种局部工具是外微分和里奇的张量分析。

An exterior differential form is the integrand of a multiple integral, such as

外微分形式是多重积分的被积表达式，例如

$${\iint }_{D}Pdydz+Qdzdx+Rdxdy\text{\hspace{1em}(7)}$$

in $(x,y,z)$-space, where $P,Q,R$ are functions in $x,y,z$ and $D$ is a two-dimensional domain. It is observed that a change of variables in $D$ (supposed to be oriented) will be taken care of automatically if the multiplication of differentials is anti-symmetric, i.e.,

在 $(x,y,z)$ 空间中，其中 $P,Q,R$ 是 $x,y,z$ 的函数，而 $D$ 是一个二维区域。观察到，如果微分的乘法是反对称的，即

$$dy\wedge dz=-dz\wedge dy,\text{etc.}\text{\hspace{1em}(8)}$$

where the symbol $\wedge$ is used to denote exterior multiplication. It is also more suggestive to introduce the exterior two - form

这里用符号 $\wedge$ 表示外积。引入外二形式会更有启发性：

$$\omega =Pdy\wedge dz+Qdz\wedge dx+Rdx\wedge dy\text{\hspace{1em}(9)}$$

and to write the integral (7) as a pairing $(D,\omega )$ of the domain $D$ and the form $\omega$.
并将积分（7）写成区域 $D$ 和形式 $\omega$ 的配对 $(D,\omega )$。

For if the same is done in $n$-space, then Stokes’s theorem can be written

如果在 $n$ 维空间中进行相同的操作，那么斯托克斯定理可以写成

$$(D,d\omega )=(\partial D,\omega )\text{\hspace{1em}(10)}$$

where $D$ is an $r$-dimensional domain and $\omega$ is an exterior $(r-1)$-form; $\partial D$ is the boundary of $D$ and $d\omega$ is the exterior derivative of $\omega$ and is an $r$-form. Formula (10), the fundamental formula in multi - variable calculus, shows that $\partial$ and $d$ are adjoint operators. The remarkable fact is that, while the boundary operator $\partial$ on domains is global, the exterior differentiation operator $d$ on forms is local. This makes $d$ a powerful tool. When applied to a function (=0-form) and a 1-form, it gives the gradient and the curl, respectively. All the smooth forms, of all degrees (dim of manifold), of a differentiable manifold constitute a ring with the exterior differentiation operator $d$. Elie Cartan used the exterior differential calculus most efficiently in local problems of differential geometry and partial differential equations. The global theory was founded by G. de Rham, after initial work of Poincare. This will be discussed in the next section.
其中，$D$ 是一个 $r$ 维区域，$\omega$ 是一个外 $(r-1)$ 形式；$\partial D$ 是 $D$ 的边界，而 $d\omega$ 是 $\omega$ 的外导数，是一个 $r$ 形式。公式（10）是多变量微积分中的基本公式，它表明 $\partial$ 和 $d$ 是伴随算子。值得注意的是，尽管在区域上的边界算子 $\partial$ 是全局的，但在形式上的外导数算子 $d$ 是局部的。这使得 $d$ 成为一个强大的工具。当它应用于函数（=0 形式）和 1 形式时，它分别给出梯度和旋度。一个可微流形的所有光滑形式（所有度数，即流形的维数）构成一个环，其外导数算子为 $d$。嘉当在微分几何和偏微分方程的局部问题中最为高效地使用了外微分。全局理论由 G. de Rham 在庞加莱的初步工作之后创立。这将在下一节中讨论。

In spite of its importance the exterior differential calculus is inadequate in describing the geometrical and analytical phenomena on a manifold. A broader concept is Ricci’s tensor analysis. Tensors are based on the fact that a manifold, being smooth, can be approximated at every point by a linear space, called its tangent space. The tangent space at a point leads to associated tensor spaces. Differentiation of tensor fields needs an additional structure, called an affine connection. If the manifold has a Riemannian or Lorentzian structure, the corresponding Levi - Civita connection will serve the purpose.
尽管外微分非常重要，但它在描述流形上的几何和分析现象时仍然不够充分。一个更广泛的概念是里奇的张量分析。张量基于这样一个事实：流形是光滑的，可以在每一点用一个线性空间来近似，这个线性空间称为切空间。一个点的切空间导致相关的张量空间。张量场的微分需要一个额外的结构，称为仿射联络。如果流形具有黎曼或洛伦兹结构，相应的列维 - 齐维塔联络将满足这一需求。

7.Homology.

同调

Historically a systematic study of the global invariants of a manifold began with combinatorial topology. The idea is to decompose the manifold into cells and see how they fit together. (The decomposition satisfies some mild conditions, which we will not specify.) In particular, if $M$ is a closed manifold of dimension $n$ and ${\alpha }_k$ denotes the number of $k$-cells of the decomposition, $k=0,1,\dots ,n$, then, as a generalization of (3), the Euler - Poincare characteristic of $M$ is defined by

从历史上看，对流形的全局不变量的系统研究始于组合拓扑学。其思想是将流形分解为单元格，并观察它们是如何组合在一起的。（这种分解满足一些温和的条件，我们在此不具体说明。）特别是，如果 $M$ 是一个 $n$ 维的闭流形，而 ${\alpha }_k$ 表示分解中的 $k$ 维单元格的数量，$k=0,1,\dots ,n$，那么，作为（3）的推广，$M$ 的欧拉 - 庞加莱特征数定义为

$$\chi (M)={\alpha }_0-{\alpha }_1+\dots +(-1{)}^n{\alpha }_n.\text{\hspace{1em}(11)}$$

The basic notion in homology theory is that of a boundary. A chain is a sum of cells with multiplicities. It is called a cycle if it has no boundary, i.e., if its boundary is zero. The boundary of a chain is a cycle (see Fig.7). The number of linearly independent $k$-dimensional cycles modulo $k$-dimensional boundaries is a finite integer $b_k$, called the $k$-th Betti number. The Euler - Poincare formula says

同调理论中的基本概念是边界。链是带有重数的单元格的和。如果它没有边界，即其边界为零，则称为循环。链的边界是一个循环（见图 7）。模 $k$ 维边界的线性独立的 $k$ 维循环的数量是一个有限整数 $b_k$，称为第 $k$ 个贝蒂数。欧拉 - 庞加莱公式表明

$$\chi (M)=b_0-b_1+\dots +(-1{)}^n{b}_n.\text{\hspace{1em}(12)}$$

The Betti numbers $b_k$ and hence $\chi (M)$ itself, are topological invariants of $M$, that is, they are independent of the decomposition and remain invariant under a topological transformation of $M$. This and more general statements could be considered the fundamental theorems of combinatorial topology. After the path - breaking works of Poincare and L.E. J. Brouwer, combinatorial topology blossomed in the U.S. in the 1920’s under the leadership of Veblen, Alexander, and Lefschetz.
贝蒂数 $b_k$ 以及 $\chi (M)$ 本身，都是 $M$ 的拓扑不变量，即它们与分解无关，并且在 $M$ 的拓扑变换下保持不变。这些以及更一般的陈述可以被视为组合拓扑学的基本定理。在庞加莱和 L.E. J. 布劳威尔的开创性工作之后，组合拓扑学在美国于 20 世纪 20 年代在维布伦、亚历山大和莱夫谢茨的领导下蓬勃发展。

While this is an effective way in deriving topological invariants, the danger in cutting a manifold is that it might be “killed.” Precisely, this means that by using a combinatorial approach we may lose sight of the relations of the topological invariants with local geometrical properties. It turns out that, while homology theory depends on the boundary operator $\partial$, there is a dual cohomology theory based on the exterior differentiation operator $d$, the latter being a local operator.
虽然这是一种推导拓扑不变量的有效方法，但对流形进行切割的危险在于它可能会被“杀死”。具体来说，这意味着通过使用组合方法，我们可能会失去对拓扑不变量与局部几何性质之间关系的洞察。事实证明，虽然同调理论依赖于边界算子 $\partial$，但存在一个基于外导数算子 $d$ 的对偶上同调理论，而后者是一个局部算子。

The resulting de Rham cohomology theory can be summarized as follows: The operator $d$ has the fundamental property that, when applied repeatedly it gives the zero form; that is, for any $k$-form $\alpha$, the exterior derivative of the $(k+1)$-form $d\alpha$ is zero. This corresponds to the geometrical fact that the boundary of any chain (or domain) has no boundary. (See (10).) A form $\alpha$ is called closed, if $d\alpha =0$. It is called a derived form, if there exists a form $\beta$, of degree $k-1$, such that it can be written $\alpha =d\beta$. Thus a derived form is always closed. Two closed forms are called cohomologous if they differ by a derived form. All the closed $k$-forms which are cohomologous to each other constitute the $k$-dimensional cohomology class. The remarkable fact is that, while the families of $k$-forms, closed $k$-forms, derived $k$-forms are immensely large, the $k$-dimensional cohomology classes constitute a finite - dimensional linear space whose dimension is the $k$-th Betti number by

德·拉姆上同调理论可以总结如下：算子 $d$ 具有这样一个基本性质，即当它反复应用时会给出零形式；也就是说，对于任何 $k$ 形式 $\alpha$，$(k+1)$ 形式 $d\alpha$ 的外导数为零。这对应于几何事实，即任何链（或区域）的边界没有边界。（见（10）。）如果 $d\alpha =0$，则称形式 $\alpha$ 为闭形式。如果存在一个 $k-1$ 次形式 $\beta$，使得可以写成 $\alpha =d\beta$，则称其为导出形式。因此，导出形式总是闭形式。如果两个闭形式相差一个导出形式，则称它们是上同调的。所有彼此上同调的闭 $k$ 形式构成了 $k$ 维上同调类。值得注意的是，尽管 $k$ 形式、闭 $k$ 形式、导出 $k$ 形式的家族极为庞大，但 $k$ 维上同调类构成了一个有限维线性空间，其维度是第 $k$ 个贝蒂数。

De Rham cohomology is the forerunner of sheaf cohomology, which was founded by J. Leray [12] and perfected and applied with great success by H. Cartan and J. - P. Serre.
德·拉姆上同调是层上同调的先驱，层上同调由 J. Leray [12] 创立，并由 H. Cartan 和 J. - P. Serre 完善并成功应用。

8.Vector fields and generalizations.

向量场及其推广

On a manifold $M$ it is natural to consider continuous vector fields, i.e., the attachment of a tangent vector to each point, varying in a continuous manner. If the Euler - Poincare characteristic $\chi (M)$ is not zero, there is at least one point of $M$ at which the vector vanishes. In other words, when the wind blows there is at least one spot on earth with no wind (for the Euler characteristic of the two - dimensional sphere is equal to 2). More precisely, at an isolated zero of a continuous vector field, an integer, called the index, can be defined, which describes to a certain extent the behavior of the vector field at the zero, i.e., whether it is a source, a sink, or otherwise. No matter what the vector field is, so long as it is continuous and has only a finite number of zeros, then the theorem of Poincare - Hopf says that the sum of its indices at all the zeros is a topological invariant which is precisely $\chi (M)$.
在一个流形 $M$ 上，自然会考虑连续向量场，即以连续方式将一个切向量附加到每个点上。如果欧拉 - 庞加莱特征数 $\chi (M)$ 不为零，那么在 $M$ 上至少有一点向量消失。换句话说，当风吹时，地球上至少有一点是没有风的（因为二维球面的欧拉特征数等于 2）。更准确地说，在连续向量场的一个孤立零点处，可以定义一个整数，称为指数，它在一定程度上描述了向量场在零点的行为，即它是源、汇还是其他。无论向量场是什么，只要它是连续的并且只有有限个零点，那么庞加莱 - 霍普夫定理表明，其所有零点处的指数之和是一个拓扑不变量，正是 $\chi (M)$。

This is a statement on the tangent bundle of $M$, i.e., the collection of the tangent spaces of $M$. More generally, a family of vector spaces parametrized by a manifold $M$ and satisfying a local product condition is called a vector bundle over $M$.
这是关于 $M$ 的切丛的陈述，即 $M$ 的切空间的集合。更一般地，由流形 $M$ 参数化的向量空间族，满足局部乘积条件，称为 $M$ 上的向量丛。

A fundamental question is whether such a bundle is globally a product. The above discussion shows that the tangent bundle is not a product if $\chi (M)\ne 0$; for if it were a product, there would exist a continuous vector field which is nowhere zero. The existence of a space which is locally but not globally a product, such as the tangent bundle of a manifold $M$ with $\chi (M)\ne 0$, is not easy to visualize; geometry thus enters a more sophisticated phase.
一个基本问题是这种丛是否是全局的乘积。上述讨论表明，如果 $\chi (M)\ne 0$，则切丛不是乘积；因为如果它是乘积，那么就会存在一个处处非零的连续向量场。一个局部是但全局不是乘积的空间的存在，例如具有 $\chi (M)\ne 0$ 的流形 $M$ 的切丛，是不容易想象的；几何学因此进入了一个更复杂的阶段。

To describe the global deviation of a vector bundle from a product space the first invariants are the so - called characteristic cohomology classes. The Euler - Poincare characteristic is the simplest of the characteristic classes.
为了描述向量丛从乘积空间的全局偏离，最初的不变量是所谓的特征上同调类。欧拉 - 庞加莱特征数是最简单的特征类。

The Gauss - Bonnet formula (4) in §4 takes the particularly simple form

第 4 节中的高斯 - 博内公式（4）具有特别简单的形式

$$\iint KdA=2\pi \chi (\Sigma )\text{\hspace{1em}(4a)}$$

when the surface has no boundary. In this formula $K$ is the Gaussian curvature and $dA$ is the element of area. Formula (4a) is of paramount importance because it expresses the global invariant $\chi (\Sigma )$ as the integral of a local invariant, which is perhaps the most desirable relationship between local and global properties. This result has a wide generalization.
当曲面没有边界时。在这个公式中，$K$ 是高斯曲率，$dA$ 是面积元素。公式（4a）极为重要，因为它将全局不变量 $\chi (\Sigma )$ 表示为局部不变量的积分，这也许是局部与全局性质之间最理想的关系。这一结果具有广泛的推广。

Let

设

$$\pi :E\to M\text{\hspace{1em}(13)}$$

be a vector bundle. The generalization of a tangent vector field on $M$ is a section of the bundle, i.e., a smooth mapping $s:M\to E$, such that the composition $\pi \circ s$ is the identity. Since $E$ is only locally a product, the differentiation of $s$ needs an additional structure, usually called a connection. The resulting differentiation, called covariant differentiation, is generally not commutative. The notion of curvature is a measure of the non - commutativity of covariant differentiation. Suitable combinations of the curvature give rise to differential forms which represent characteristic cohomology classes in the sense of the de Rham theory, of which the Gauss - Bonnet formula (4a) is the simplest example [13]. I believe that the concepts of vector bundles, connections, and curvature are so fundamental and so simple that they should be included in any introductory course on multivariable calculus.
是一个向量丛。在 $M$ 上的切向量场的推广是丛的一个截面，即一个光滑映射 $s:M\to E$，使得复合映射 $\pi \circ s$ 是恒等映射。由于 $E$ 只是局部的乘积，对 $s$ 的微分需要一个额外的结构，通常称为联络。由此产生的微分，称为协变微分，通常不是可交换的。曲率的概念是协变微分不可交换性的度量。曲率的适当组合会产生微分形式，这些微分形式代表德·拉姆理论意义上的特征上同调类，其中高斯 - 博内公式（4a）是最简单的例子 [13]。我相信，向量丛、联络和曲率的概念是如此基本且简单，应该包含在任何多元微积分的入门课程中。

9.Elliptic differential equations.

椭圆型微分方程

When $M$ has a Riemannian metric, there is an operator $\ast$ sending a $k$-form $\alpha$ to the $(n-k)$-form $\ast \alpha$, $n=\dim M$. It corresponds to the geometrical construction of taking the orthogonal complement of a linear subspace of the tangent space. With $\ast$ and the differential $d$ we introduce the codifferential

当 $M$ 具有黎曼度量时，存在一个算子 $\ast$，将一个 $k$ 形式 $\alpha$ 发送到 $(n-k)$ 形式 $\ast \alpha$，$n=\dim M$。它对应于取切空间的线性子空间的正交补的几何构造。通过 $\ast$ 和微分 $d$，我们引入余微分

$$\delta =(-1{)}^{nk+n+1}\ast d\ast \text{\hspace{1em}(14)}$$

and the Laplacian

和拉普拉斯算子

$$\Delta =d\delta +\delta d.\text{\hspace{1em}(15)}$$

Then the operator $\delta$ sends a $k$-form to a $(k-1)$-form and $\Delta$ sends a $k$-form to a $k$-form. A form $\alpha$ satisfying

那么，算子 $\delta$ 将一个 $k$ 形式发送到一个 $(k-1)$ 形式，而 $\Delta$ 将一个 $k$ 形式发送到一个 $k$ 形式。满足

$$\Delta \alpha =0\text{\hspace{1em}(16)}$$

is called harmonic. A harmonic form of degree 0 is a harmonic function in the usual sense. The equation (16) is an elliptic partial differential equation of the second order. If $M$ is closed, all its solutions form a finite dimensional vector space. By a classical theorem of Hodge this dimension is exactly the $k$-th Betti number $b_k$. It follows by (12) that the Euler characteristic can be written

的称为调和形式。0 次调和形式是通常意义上的调和函数。方程（16）是一个二阶椭圆型偏微分方程。如果 $M$ 是闭的，那么它的所有解构成一个有限维向量空间。根据霍奇的经典定理，这个维度正好是第 $k$ 个贝蒂数 $b_k$。根据（12），欧拉特征数可以写成

$$\chi (M)=d_e-d_0,\text{\hspace{1em}(17)}$$

where $b_{\text{even}}$ (respectively, $b_{\text{odd}}$) is the dimension of the space of harmonic forms of even (respectively, odd) degree. The exterior derivative $d$ is itself an elliptic operator and (17) can be regarded as expressing $\chi (M)$ as the index of an elliptic operator. The latter is, for any linear elliptic operator, equal to the dimension of the space of solutions minus the dimension of the space of solutions of the adjoint operator.
其中，$b_{\text{even}}$（分别地，$b_{\text{odd}}$）是偶（分别地，奇）次调和形式空间的维度。外导数 $d$ 本身是一个椭圆算子，（17）可以被视为将 $\chi (M)$ 表示为椭圆算子的指标。对于任何线性椭圆算子，后者等于解空间的维度减去伴随算子的解空间的维度。

The expression of the index of an elliptic operator as the integral of a local invariant culminates in the Atiyah - Singer index theorem. It includes as special cases many famous theorems, such as the Hodge signature theorem, the Hirzebruch signature theorem, and the Riemann - Roch theorem for complex manifolds. An important by - product of this study is the recognition of the need to consider pseudo - differential operators on manifolds, which are more general than differential operators.
将椭圆算子的指标表示为局部不变量的积分，最终导致了阿蒂亚 - 辛格指标定理。它包括许多著名的定理作为特殊情况，如霍奇符号定理、希策布鲁赫符号定理和复流形的黎曼 - 罗赫定理。这一研究的一个重要副产品是认识到需要考虑流形上的伪微分算子，它们比微分算子更为一般。

Elliptic differential equations and systems are closely enmeshed with geometry. The Cauchy - Riemann differential equations, in one or more complex variables, are at the foundation of complex geometry. Minimal varieties are solutions of the Euler - Lagrange equations of the variational problem minimizing the area. These equations are quasi - linear. Perhaps the “most” non - linear equations are the Monge - Ampere equations, which are of importance in several geometrical problems. Great progress has been made in these areas in recent years [14]. With this heavy intrusion of analysis George Birkhoff’s remark quoted above sounds even more disturbing. However, while analysis maps a whole mine, geometry looks out for the beautiful stones. Geometry is based on the principle that not all structures are equal and not all equations are equal.
椭圆型微分方程和方程组与几何学密切相关。在单个或多个复变量中的柯西 - 黎曼微分方程是复几何学的基础。极小曲面是面积最小化变分问题的欧拉 - 拉格朗日方程的解。这些方程是拟线性的。也许“最”非线性的方程是蒙日 - 安培方程，在许多几何问题中具有重要意义。近年来在这些领域取得了巨大进展 [14]。在这种分析的大量介入下，上面引用的乔治·伯克霍夫的评论听起来更加令人不安。然而，尽管分析绘制了一座完整的矿山，几何学却在寻找美丽的石头。几何学基于这样一个原则：并非所有结构都是平等的，并非所有方程都是平等的。

10.Euler characteristic as a source of global invariants.

欧拉特征数作为全局不变量的来源

To summarize, the Euler characteristic is the source and common cause of a large number of geometrical disciplines. I will illustrate this relationship by a diagram. (See Fig.8.)

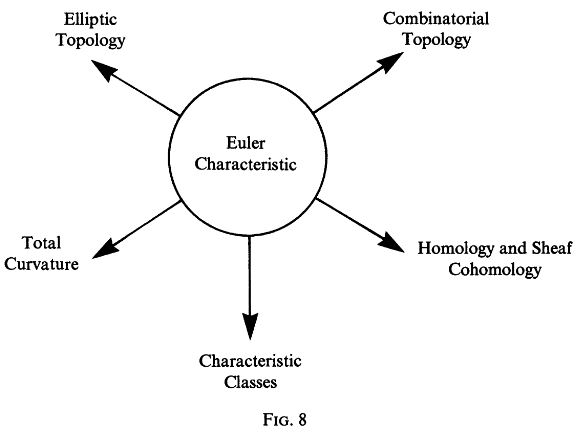
总结来说，欧拉特征数是众多几何学科的根源和共同原因。我将通过一幅图来说明这种关系。（见图 8）

11.Gauge field theory.

规范场论

At the beginning of this century differential geometry got the spotlight through Einstein’s theory of relativity. Einstein’s idea was to interpret physical phenomena as geometrical phenomena and to construct a space which would fit the physical world. It was a gigantic task and it is not clear whether he said the last word on a unified field theory of gravitational and electromagnetic fields. The introduction of vector bundles described above, and particularly the connections in them with their characteristic classes and their relations to curvature, widened the horizon of geometry. The case of a line bundle (i.e., when the fiber is a complex line) furnishes the mathematical basis of Weyl’s gauge theory of an electromagnetic field. The Yang - Mills theory, based on an understanding of the isotopic spin, is the first example of a nonabelian gauge theory. Its geometrical foundation is a complex plane bundle with a unitary connection. Attempts to unify all field theories, including strong and weak interactions, have recently focused on a gauge theory, i.e., a geometrical model based on bundles and connections. It is with great satisfaction to see geometry and physics united again.
在本世纪初，微分几何通过爱因斯坦的相对论而受到关注。爱因斯坦的想法是将物理现象解释为几何现象，并构建一个适合物理世界的几何空间。这是一个巨大的任务，目前还不清楚他是否对引力场和电磁场的统一场论说了最后的话。上述引入的向量丛，特别是其中的联络及其特征类以及它们与曲率的关系，拓宽了几何学的视野。线丛的情况（即纤维是复线）为外尔的电磁场规范理论提供了数学基础。基于对同位旋的理解，杨 - 米尔斯理论是非阿贝尔规范理论的第一个例子。其几何基础是一个具有酉联络的复平面丛。最近，试图统一所有场论（包括强相互作用和弱相互作用）的努力集中在规范理论，即基于丛和联络的几何模型。看到几何学和物理学再次统一，令人非常欣慰。

Bundles, connections, cohomology, characteristic classes are sophisticated concepts which crystallized after long years of search and experimentation in geometry. The physicist C. N. Yang wrote [15]: “That nonabelian gauge fields are conceptually identical to ideas in the beautiful theory of fiber bundles, developed by mathematicians without reference to the physical world, was a great marvel to me.” In 1975 he mentioned to me: “This is both thrilling and puzzling, since you mathematicians dreamed up these concepts out of nowhere.” This puzzling is mutual. In fact, referring to the role of mathematics in physics, Eugene Wigner spoke about the unreasonable effectiveness of mathematics [16]. If one has to find a reason, it might be expressed in the vague term “unity of science.” Fundamental concepts are always rare.
丛、联络、上同调、特征类是复杂的概念，它们是在几何学中经过多年的探索和实验后形成的。物理学家杨振宁写道 [15]：“非阿贝尔规范场在概念上与数学家在不涉及物理世界的情况下发展起来的纤维丛理论中的思想完全一致，这对我来说是一个巨大的奇迹。”1975 年，他对我提到：“这既令人兴奋又令人困惑，因为你们数学家凭空想出了这些概念。”这种困惑是相互的。事实上，尤金·维格纳在谈到数学在物理学中的作用时，曾提到数学的不合理有效性 [16]。如果非要找一个原因，可能可以用“科学的统一性”这个模糊的术语来表达。基本概念总是稀少的。

Concluding remarks.

结束语

Modern differential geometry is a young subject. Not counting the strong impetus it received from relativity and topology, its developments have been continuous. I am glad that we do not know what it is and, unlike many other mathematical disciplines, I hope it will not be axiomatized. With its contact with other domains in and outside of mathematics and with its spirit of relating the local and the global, it will remain a fertile area for years to come.
现代微分几何是一门年轻的学科。不计算它从相对论和拓扑学中得到的强大推动，它的发展一直是连续的。我很高兴我们不知道它是什么，并且与其他许多数学学科不同，我希望它不会被公理化。由于它与其他数学领域内外的联系以及它将局部与整体联系起来的精神，它将在未来许多年里保持肥沃。

It may be interesting to characterize a period of mathematics by the number of variables in the functions or the dimension of the spaces it deals with. In this sense nineteenth century mathematics is one - dimensional and twentieth century mathematics is $n$ - dimensional. It is because of the multi - variables that algebra acquires paramount importance. So far most of the global results on manifolds are concerned with even - dimensional ones. In particular, all complex algebraic varieties are of even real dimension. Odd - dimensional manifolds are still very mysterious. I venture to hope that they will receive more attention and substantial clarification in the twenty - first century. Recent works on hyperbolic 3 - manifolds by W. Thurston [17] and on closed minimal surfaces in a 3 - manifold by S. T. Yau, W. Meeks, and R. Schoen have thrown considerable light on 3 - manifolds and their geometry. Perhaps the problem of problems in geometry is still the so - called Poincare conjecture which says that a closed simply connected 3 - dimensional manifold is homeomorphic to the 3 - sphere. Topological and algebraic methods have so far not led to a clarification of this problem. It is conceivable that tools in geometry and analysis will be found useful.
通过函数中的变量数量或所涉及空间的维度来描述一个数学时期可能是有趣的。在这个意义上，19 世纪的数学是一维的，而 20 世纪的数学是 $n$ 维的。正是由于多变量的存在，代数才变得至关重要。到目前为止，关于流形的大多数全局结果都涉及偶数维流形。特别是，所有复代数簇都是偶数实维的。奇数维流形仍然非常神秘。我冒险希望它们在 21 世纪会受到更多关注并得到实质性的澄清。W. Thurston [17] 关于双曲 3 - 流形的近期工作，以及 S. T. Yau、W. Meeks 和 R. Schoen 关于 3 - 流形中闭极小曲面的研究，为 3 - 流形及其几何学提供了大量的启示。也许几何学中最大的问题是所谓的庞加莱猜想，即一个闭的单连通 3 维流形与 3 维球面同胚。到目前为止，拓扑和代数方法还没有澄清这个问题。可以想象，几何和分析中的工具将被证明是有用的。

This paper, written with partial support from NSF Grant MCS77 - 23579, was delivered as a Faculty Research Lecture at Berkeley, California, on April 27, 1978.
本文在 NSF 资助项目 MCS77 - 23579 的部分支持下撰写，并于 1978 年 4 月 27 日在加利福尼亚州伯克利的教员研究讲座上发表。

References

参考文献

1. O. Veblen and J. H. C. Whitehead, Foundations of Differential Geometry, Cambridge, England, 1932, p. 17.
   O. Veblen 和 J. H. C. Whitehead，《微分几何基础》，英国剑桥，1932 年，第 17 页。

2. Elie Cartan, Le rôle de la théorie des groupes de Lie dans l’évolution de la géométrie moderne, Congrès Inter.Math., Oslo, 1936, Tome I, p. 96.
   Elie Cartan，《李群理论在现代几何学发展中的作用》，奥斯陆国际数学家大会，1936 年，第一卷，第 96 页。

3. George D. Birkhoff, Fifty years of American mathematics, Semicentennial Addresses of Amer. Math. Soc., 1938, p. 307.
   George D. Birkhoff，《五十年美国数学》，美国数学会半世纪演讲集，1938 年，第 307 页。

4. A. Weil, S. S. Chern as friend and geometer, Chern, Selected Papers, Springer Verlag, New York, 1978, p. xi.
   A. Weil，《陈省身：朋友与几何学家》，《陈省身文选》，纽约斯普林格出版社，1978 年，第 xi 页。

5. H. Whitney, On regular closed curves in the plane, Comp. Math. 4 (1937), 276 - 284.
   H. Whitney，《平面上的正则闭曲线》，《数学计算》4（1937），第 276 - 284 页。

6. William F. Pohl and George W. Roberts, Topological considerations in the theory of replication of DNA, Journal of Mathematical Biology, 6 (1978), 383 - 386, 402.
   William F. Pohl 和 George W. Roberts，《DNA 复制理论中的拓扑考虑》，《数学生物学杂志》，6（1978），第 383 - 386 页，第 402 页。

7. James H. White, Self - linking and the Gauss integral in higher dimensions, American J. of Math., 91 (1969), 693 - 728; B. Fuller, The writhing number of a space curve, Proc. Nat. Acad. Sci., 68 (1971), 815 - 819; F. Crick, Linking numbers and nucleosomes, Proc. Nat. Acad. Sci., 73 (1976), 2639 - 2643.
   James H. White，《自身环绕与高维中的高斯积分》，《美国数学杂志》，91（1969），第 693 - 728 页；B. Fuller，《空间曲线的缠结数》，《美国国家科学院院刊》，68（1971），第 815 - 819 页；F. Crick，《环绕数与核小体》，《美国国家科学院院刊》，73（1976），第 2639 - 2643 页。

8. S. Smale, A classification of immersions of the two - sphere, Transactions AMS, 90 (1959), 281 - 290; cf. also A. Phillips, Turning a surface inside out, Scientific American, 214 (May 1966), 112 - 120. A film of the process, by N. L. Max, is distributed by International Film Bureau, Chicago, IL.
   S. Smale，《二维球面浸入的分类》，《美国数学会会刊》，90（1959），第 281 - 290 页；另见 A. Phillips，《翻转一个曲面》，《科学美国人》，214（1966 年 5 月），第 112 - 120 页。由 N. L. Max 制作的该过程的影片由芝加哥国际影片局发行。

9. H. Weyl, Philosophy of Mathematics and Science, 1949, p. 90.
   H. Weyl，《数学与科学哲学》，1949 年，第 90 页。

10. A. Einstein, Library of Living Philosophers, vol. I, p. 67.
    A. Einstein，《在世哲学家文库》，第 1 卷，第 67 页。

11. J. Hadamard, Psychology of Invention in the Mathematical Field, Princeton, 1945, p. 115.
    J. Hadamard，《数学领域的发明心理学》，普林斯顿，1945 年，第 115 页。

12. R. Godement, Topologie algébrique et théorie des faisceaux, Hermann, Paris, 1958.
    R. Godement，《代数拓扑与层理论》，巴黎赫尔曼出版社，1958 年。

13. S. Chern, Geometry of characteristic classes, Proc. 13th Biennial Sem. Canadian Math. Congress, 140 (1972).
    S. Chern，《特征类的几何》，加拿大数学大会第 13 届双年研讨会论文集，140（1972）。

14. S. T. Yau, The role of partial differential equations in differential geometry, Int. Congress of Math., Helsinki, 1978.
    S. T. Yau，《偏微分方程在微分几何中的作用》，赫尔辛基国际数学家大会，1978 年。

15. C. N. Yang, Magnetic monopoles, fiber bundles, and gauge fields, Annals of the New York Academy of Sciences, 294 (1977), 86 - 97.
    C. N. Yang，《磁单极子、纤维丛和规范场》，纽约科学院学报，294（1977），第 86 - 97 页。

16. E. Wigner, The unreasonable effectiveness of mathematics in the natural sciences, Communications on Pure and Applied Math., 13 (1960), 1 - 14.
    E. Wigner，《数学在自然科学中的不合理有效性》，《纯数学与应用数学通讯》，13（1960），第 1 - 14 页。

17. W. Thurston, Geometry and topology in dimension three, Int. Congress of Math., Helsinki, 1978.
    W. Thurston，《三维中的几何与拓扑》，赫尔辛基国际数学家大会，1978 年。

DEPARTMENT OF MATHEMATICS, UNIVERSITY OF CALIFORNIA, BERKELEY, CA 94720.

美国加利福尼亚大学伯克利分校数学系，加利福尼亚州伯克利，邮编 94720。

---

陈省身：数学陶冶我一生

陈省身 赛先生 2024 年 12 月 28 日 17:02 广东

数学家陈省身（1911 年 10 月 26 日 - 2004 年 12 月 3 日）图源：陈省身数学研究所

导读：

陈省身，1911 年 10 月 28 日生于浙江嘉兴秀水，1930 年毕业于南开大学，是 20 世纪最伟大的几何学家之一。他发展了 Gauss—Bonnet (高斯一博内) 公式，被命名为 “Gauss－Bonnet－陈省身公式”，提出了 “陈氏示性类 (Chern Class)”，成为经典杰作。他发展了微分纤维丛理论，其影响遍及数学的各个领域。他创立了复流形上的值分布理论，包括 Bott－陈定理，影响及于代数论。他为广义的积分几何奠定基础，获得基本运动学公式。他所引入的陈氏示性类与陈－Simons 微分式，已深入到数学以外的其他领域，成为理论物理的重要工具。他在整体微分几何上的卓越贡献，影响了整个数学的发展，被誉为继欧几里德、高斯、黎曼、嘉当之后又一里程碑式的人物。他曾先后主持创办了原中央研究院数学研究所、美国国家数学研究所、南开数学研究所三大数学研究所，造就了一批世界知名的数学家。

2024 年是陈省身先生去世 20 周年，《赛先生》特转载陈先生自述，以兹纪念。

陈省身 | 撰文

早年在中国所受的教育

我于 1923 年 1 月进天津扶轮中学。那是一所四年制的高级中学，我获准插班入一年级就读第二学期。该校的数学课程有：

（1）第一年，算术，使用中文课本；
（2）第二年，代数，使用 Hall 与 Knight 的课本；
（3）第三年，几何，使用 Wentworth 与 Smith 的课本；
（4）第四年，三角学和高级代数，分别使用 Wentworth-Smith 及 Hall-Knight 的课本。

我的老师都很有能力，又极富献身精神，我做了大量习题。到第四年，我已能做许多 Hall-Knight 的书中引用的剑桥大学荣誉学位考试的题目。

1926 年我从扶轮毕业；同年我进南开大学，实际上是跳了两级，因此我从未上过解析几何课。更糟的是，我必须参加南开大学的入学考试，其数学试题中解析几何占很重的份量。

考试前的三个星期，我自学了 Young 与 Morgen 的《数学分析》（Mathematical analysis）如果记得不错的话，我的考卷位列第二。不过在很长的一段时间内，「圆锥曲线的焦点」这一概念令我大伤脑筋，直到几年后学了射影几何学我才茅塞顿开。

进南开大学后，我很快就发现自己做实验笨手笨脚，于是数学便成为我唯一的选择。我有幸得姜立夫教授为师，他 1918 年获哈佛大学哲学博士学位，导师是 J. Coolidge，论文题目是关于非欧几里得空间中线球接触变换的。

因此，我在大学第四年，花了许多功夫学几何，所读的书中有 Coolidge 的《非欧几何学》（Noneuclidean Geometry）与《圆和球的几何学》（Geometry of the circle and sphere），Solmon 的《圆锥曲线》（conic sections）与《立体解析几何》（Analytic Geometry of Three Dimmensions），以及 Castelnuovo 的《解析几何与射影几何》（Analytic and Projective Geometry）等。

尤其使我着迷的是 Otto Staude 的二卷本着作《线构造》（Fadenkonstruktionen）。二次超曲面的几何是数学中优美的篇章。我很高兴看到 J. Moser1979 年在可积哈密顿系统和谱理论的研究中继续这方面的工作。（参见 3）甚至在今日，研究 Salmon 的东西可能仍是有价值的，至少在我看来是有趣的。

1930 年我从南开毕业，去北平清华大学从孙鎕教授工作。孙先生在当时是中国发表数学研究论文的唯一的数学家。孙的研究领域是射影微分几何，他曾是芝加哥大学 E.P.Lane 的博士生。

这个主题由 E.J. Wilczynsky 于 1901 年创立，是那时已经支配几何学近一世纪的射影几何的一个自然产物。我熟悉了这方面的文献，并写了几篇论文，其中包括我的有关射影线几何的硕士论文。

继 Plücker 与 Klein 之后，线几何一直是几何学家们喜爱的主题。事实上，Klein 的学位论文就是关于二次线体的，即 Plücker 坐标下的二次方程所确定的线轨（line loci）。二次线体具有许多背景中也有许多线几何的内容。

我的论文研究线汇，即线的二维子流形以及它们的通过二次线体的密切（osculation）。

在我的研究生学业接近结束时，即大约 1934 年左右，我开始认识到整体微分几何（当时称为大范围微分几何）的重要性。我的主要灵感来自 W. Blaschke 的关于微分几何的那些著作。

很清楚，代数拓扑是整个领域的基础。而代数拓扑本身当时还处于发展阶段。Veblen 于 1922 年发表的 analysis situs 引进了「同调不变量」（homology characters）即根据关联矩阵得出的 Betti 数和挠系数。Lefschetz 的《拓扑学》于 1930 年出版，但该书对初学者进入这个领域并无裨益。

我曾听过 Emanuel Sperner 的讲课（1933～1934 年）。当时 Sperner 正在北京大学访问，他的课包含有对 Erhard Schmidt 关于约当曲线定理的证明的严密而详细的论述。

我也听过江泽涵讲授的以 Lefschetz 的书为蓝本的「位置分析」课，江是 Marston Morse 过去的学生，曾担任 Lefschetz 的助手。而我当时的感觉是我只是刚刚站在代数拓扑这座伟大殿堂的门口。到 1934 年 Seifert-Threlfall 的书和 1935 年 Alexandroff-Hopf 的书问世，情况才有了巨大的变化。

1932 年春季，Blaschke 访问了北平，作了关于「微分几何中的拓扑问题」的系列演讲。这是真正的局部微分几何。他采用全体微分同胚构成的伪群取代经典微分几何中的李群，并研究了局部不变量。

我能跟上 Blaschke 的演讲并去阅读发表在汉堡大学数学讨论会论文集（Hamburger Abhandlungen）及其它杂志上的包含在这同一个总标题下的许多论文。这个主题现在称为网几何（web geometry）。由于有此接触，之前又已掌握 Blaschke 的微分几何书中的知识，所以当 1934 年获得一笔奖学金时，我决定去汉堡留学。

欧洲的留学生活

1934 年～1936 年我在汉堡，1936 年获理学博士学位；并曾在巴黎随 Elie Cartan 从事一年博士后研究，去汉堡的选择实属幸运之举。汉堡大学有一个很强的数学系，Blaschke、Artin 以及 Hecke 是那里的教授，较资浅的成员包括 E. Kähler、H. Petersson 和 H. Zassenhaus。

那时 Blaschke 的数学兴趣正从网几何转向积分几何。1934 年 9 月我刚见到他时，他给了我一大叠关于网几何的抽印本。我开始对网的秩的概念和具有最大的秩的网产生了兴趣。大家知道，${\mathbb{R}}^n$ 中一个余维是 1 的 d - 网由处于一般位置的 d 个超曲面叶结构组成。

设 $x_1,...,x_n$ 是 ${\mathbb{R}}^n$ 的坐标，叶状结构由方程 $u_i(x_1,...,x_n)=\text{常数}$（$1\le i\le d$）给定。形如 $\sum _{1\le i\le d}{f}_i(u_i)=0$ 的方程被称为是 Abel 方程。线性无关的 Abel 方程的最大个数被称为是这个网的秩。如果 d - 网由 ${\mathbb{R}}^n$ 空间里的 d 类代数曲线的超平面定义，它就具有这样的 Abel 方程，它们是将 Abel 定理应用 Abel 微分获得的。因而这个 d - 网的秩至少是该曲线的亏格（genus)。

在一篇短文中我确定了 ${\mathbb{R}}^n$ 中所有余维为 1 的 d - 网的最大秩。根据 Castelnuovo 的一个定理，这个整数等于 n 维射影空间 Pn 里不属于任意超平面 Pn-1 的 d 次代数曲线的最大亏格。

值得注意的事实是，并非所有具有最大秩的网都是由上述方式描述的具有最大亏格的代数曲线给出的；这里存在怪异的具有最大秩的网，这些网的叶并非都是超平面。这些 Abel 方程本质上是函数方程，因为在经典情形中，这些方程变成众所周知的超越函数的加法定理。

在平面上（n=2），曲线的 5 - 网的最大秩为 6，而且存在一个怪异网（Bol 网），这个网的 Abel 方程含二重对数。1978 年 Griffiths 和我研究了 ${\mathbb{R}}^n$ 中具有最大秩且余维为 1 的 d - 网问题，但我们没有获得最后结果。我认为确定这样的怪异网是一个非常有趣且很重要的问题。

1934 年～1935 年间我的主要精力用于参加 Kähler 的讨论班。讨论班以 Kähler 刚出版不久的著名小册子《微分方程组理论导引》（Einführung in die Theorie Systeme von Differentialgleichangen）为基础。主要成果就是后来所称的 Cartan-Kähler 定理。

所有的人，包括 Blaschke、Artin 与 Hecke，都出席了首次讨论会，每人还得到一本上述的小册子。但参加者减少得很快，我是坚持到底的极少数人之一。我把这一理论用于 ${\mathbb{R}}^{2r}$ 中 r 维子流形的 3 - 网。Blaschke 和 Kähler 都认为这个结果与我先前关于最大秩的结果已足够写成一篇学位论文了。到 1935 年底我的学位论文已准备就绪。

Blaschke 及其学派主要关心积分几何，Blaschke 开过积分几何的课程。这一主题最漂亮的结果是由 L.A. Santalò 发现的。一个结果是用正项的无穷和表示平面凸曲线的等周亏量，其中每个正项均具几何意义。Santalò 的工作使他成为积分几何方面的世界级领袖。他原籍西班牙，后来移民到阿根廷。

我的另一位学友是代数几何学家周炜良，他为了跟 Hermann Weyl 做研究从芝加哥来到哥廷根。但是哥廷根乃至整个德国政局的变化使这一愿望成为泡影，他又转往莱比锡随 Van der Waerden 工作。由于某种原因，他住在汉堡，有时来参加讨论班。

周炜良当时正在发展他的「配型」（zugeordnete Formen），即后来所称「周氏坐标」。周是一位有创见的数学家。他对代数几何作出了重要贡献，包括他的紧子簇定理和相交理论。周出身于中国一个高层官宦家族，它很早就认识到西化的必要，因此这个家族出了不少杰出人物。周习惯夜间工作。当他来访时我就得牺牲一些睡眠，但却学得一些数学。

无论如何，只要可能，我就去听 Artin 的讲课。二年间他开过的课包括复变函数论、代数拓扑、相对论和丢番图逼近等。我还听过 Hecke 主要按他的书讲的代数数论课。我在汉堡的学术生涯是很理想的，但是政局不允许这种生活继续下去。

1936 年～1937 年我可从事一年博士后研究。当我征求 Blaschke 的意见时，他建议我或继续留汉堡跟 Artin 研究数论，或去巴黎跟随 Elie Cartan。这两个方案都有吸引力，我最后选择了后者。

这一抉择非常理想。那年 Cartan 开了一门外微分系统的课程；讲义后来以书的形式出版了。那些后来成为 Bourbaki 的「年轻的」法国数学家开始活跃起来。他们组织了一个「Julia 讨论班」，每二周聚一次，致力于对每年选定的一个专题进行研究。1936 年～1937 年的专题是「E. Cartan 的工作」。

Cartan 是位极好的导师。他提出的「小」问题，有些成为我论文的主题。大概由于我对他所提问题作的解答，他允许我大约每二周去他家一次。见面后的第二天我通常会收到他的信，信中往往说：「你走后我又考虑了他的问题。… 这问题似乎很有趣…」这一年过得有趣而令人难忘。

我还听过 Montel 有关多复变的讲课，参加过 Hadamard 在法兰西学院举办的讨论班。在每次讨论班结束时 Hadamard 总会作总结，它通常比讨论班上的演讲本身更清楚更丰富。

在获悉中日战争爆发的消息后，我怀着沉重的心情于 1937 年 7 月 10 日告别巴黎返回中国。

数学上与世隔绝

1937 年夏我离欧返华时，本打算去北平就任清华大学教授之职，由于中日战争之故，十年后才达到此目的。当时清华大学先搬到长沙，1938 年又迁至昆明，在那儿一直滞留到 1945 年夏战争结束。

昆明是座美丽的城市。虽然处于战事中的国家物资匮乏、局势动荡，但在生活的其它方面倒是愉快的。清华大学与北京大学、南开大学联合，组成了西南联合大学，昆明立刻成为战时中国知识界的中心。我的数学同仁包括华罗庚和许宝騄。我开了代数拓扑、李群、球几何及外微分系统等方面的课程和讨论班，吸引了一批学生。

主要的不便是此地与外界的联系被切断了：有段时间连「缅甸信道」也关闭了，与外界的联系只有靠空运。我有个私人小书库。起初，我做了以前想做而没时间做的事：读了些书，思考些问题，还觉得有趣。

但挫折很快就降临了，而且必须克服。我将此情信告 E. Cartan，他寄给我许多他的抽印本，包括一些过去的论文。我花了大量时间研读这些论文，考虑其内涵及应用。这确实使我受益匪浅。

在 30 年代，人们已开始认识到 Cartan 的工作的重要性，如 Weyl、Blaschke 和 Kähler，但几乎没有人去读 Cartan 旧时的论文（有关李代数的论文除外）。我很幸运能因环境之故把这些论文都遍读无遗。

驻华盛顿的中国大使胡适博士空邮来一本 Hurewicz-Wallman 写的有关《维数论》的书。现今习惯于静电复印的人也许很难想象我把除最后一章外的整本书抄了一遍。在最后一章中，作者是在没有正合序列概念的情况下处理正合序列的问题，我觉得很难理解。其实当时读论文作笔记是很普通的。复印大量资料并不能说明自己取得了多少进步。

我开始有了一些学生，其中有王宪钟和严志达。王后来对拓扑学作出了许多贡献，尽管他最出名的成果是王序列。严最早给出所有例外李群的 Betti 数的正确值。

回首往事，我并不认为自已对作为整体的数学有完善的见地。我清楚自己的某些不足并渴望得到充实。我的数学实力在于我能算。至今我不在乎繁复的计算，直到数年前我做这样的计算还很少出现差错。这方面的训练现在不大流行，也得不到鼓励，但在处理许多问题时它仍有很大的好处。

Gauss-Bonnet 公式曾使我着迷，我知道它的最概念化的证明是通过结构方程来表示联络形式的外微分。当 1943 年我去普林斯顿时，它已为为我在数学工作中最得意的一篇论文开了题。

普林斯顿阳光灿烂

我于 1943 年 8 月抵达普林斯顿。气氛的变化令人难忘。那段日子高等研究院很清静，大多数人已离去为战事服务。

Hermann Weyl 对我的工作很感兴趣。我访问之前他曾为《数学纪事》（Annals of Mathematics）审阅过我一篇有关迷向曲面的论文，并写了一个很长的给予好评的报告。这件事是他亲自泄露给我的。报告提出了改进的建议，这说明他仔细地看了全文。我们经常交谈。Weyl 的深刻洞察之一是预言代数几何有非常美好的前景。

Andre Weil 那时在附近的 Lehigh 大学，我们很快就见了面并有好多可谈的内容。当时 Weil 刚刚发表与 Allendoerfer 合作的关于 Gauss-Bonnet 公式的论文，它立刻成为我们讨论的话题。

根据我对二维情况的埋解，我知道正确的证明应该建基于我们现在称之为超度（transgression）的概念之上。困难则有两个：

（1）当时我对关于向量场的奇点的 Poincare-Hopf 定理不甚清楚；

（2）超度必须在单位切丛中而不是在主丛中实现，这就涉及到一个不平凡的技术困难。

这两个困难我都在短时间克服了，事情有了一个满意的结果。我仍认为这是我做得最好的工作。

其后自然要把这个结果扩展到 Stiefel-Whitney 类。那时即使在普林斯顿，谈起纤维丛也必得从定义开始。那时没有矢量丛，只有球丛。我注意到复示性类较简单，容许局部曲率表示。这项工作不难，但它并非那个时代拓扑学的时尚课题。

我虽是高等研究院的成员，但很多时间是在普林斯顿大学的范氏大楼度过的。Chevalley 那时正在写他的有关李群的书。Lefschetz 则固执己见，他不愿用当时盛行的常规方法研究微分几何。当时请我为《数学纪事》审阅一篇论文而建议退稿后，他让我担任该刊的副主编（associate editor）。

普林斯顿的环境与工作节拍令我十分惬意。我对数学的看法成熟多了。留居普林斯顿的日子使我感到极大的乐趣。近年来科学竞争已使科学家的生活大煞风景，尽管在数学方面的情况要好得多。我认为没有非要如此快地出成果的必要，我也不为电子邮件的发现所动。

1945 年底我告别普林斯顿回中国。踏上故土立即受命组建中国的科学院，即中央研究院的数学研究院，其时二次大战虽已结束，中国却由于内战而处于分裂状态。我向 Hermann Weyl 发出访华邀请，他欣然接受。但是中国当时的形势使这一访问未能实现。

1948 年底南京政府处于崩溃之中，感谢高等研究院主动安排我离华。1949 年冬季学期我在高等研究院，是 Veblen 的微分几何讨论班的主讲人。讲稿两年后补写出来，流传甚广。

这些讲稿现收录在已出版的我的《论文选集》第四卷内。主要结果是 Weil 同态。这是陈类从酉群到任意李群的一个推广。1944 年我在写有关复示性类的论文时就知道这个结果；由于未熟练掌握李群，当时未能证明它。Weil 通过考虑联络族，提供了一个关键性的思想。我把这个结果称为 Weil 同态。朋友们认为我应该分享这一荣誉，对此我自然不持异议。

数学上进入不惑之年

二次大战后，Marshall Stone 应召重组芝加哥大学数学系，并任系主任。他最早发出的两份聘约分别送达 Hassler Whitney 与 Andre Weil，这是他洞鉴数学与数学界的一个证明。Whitney 谢绝了，而 Weil 经过数次协商后接受了。

我在中国时 Stone 就曾写信给我谈起要在芝加哥为我提供一个讯问职位的事。1949 年我来美国后，芝加哥大学数学系决定长期聘我。我认为芝加哥大学是美国唯一的其主要目标是「知识进步」而非教育的大学。我有许多朋友在那里的数学系；1949 年夏我成了该系的成员。由此引出了一段愉快而有益的合作。

1949 年～1950 学年我开了一门名为「大范围微分几何」的课程，有一批才华横溢的学生。我自己正在开辟自己的道路，我的学生及时更正了我的许多错误和疏忽，这是生气勃勃而又有趣的结合。我还记得 Arnord Shapiro，他曾主持许多这样的讨论。

回想起来，当时我对微分几何的了解还是初步的。这门学科中一些争论问题至今未决，也许正反映了它的力量之所在。例如，曲面是什么？是嵌入还是浸入，或是由可能有奇点的方程所定义的？另一方面，我的课上涉及的许多课题，也获得了新的多方面的发展。

我与 Weil 联系密切。他随时都有准备，随时都可合作。在与我讨论过数学的众多数学家中，Weil 是极少数能迅速抓全我的思想并给予有益的评说的数学家之一。我们常沿着密执安湖畔长时间的漫步，这在当时还很安全。

我对代数拓扑也感兴趣，偶尔开一门这方面的课。我与 Ed Spanier 在球丛的研究上进行过合作。所获结果之一是把 Gysin 的工作写成一个正合序列。Rene Thom 把它做得更明白化了，这个结果现在通常称为 Thom 同构。

我觉得芝加哥和汉堡都非常令人愉快。我认为两者的规模都很合适。不幸的是数学的发展已使一切都膨胀了。

在西海岸定居

1960 年我迁往伯克利（Berkeley）。对我来说这地方并不陌生。我在中国的老师姜立夫教授就是在伯克利获得理学学位的。1946 年和 1949 年我曾两度驻足伯克利并在伯克利数学系呆过一段时间。

伯克利数学系是第一流的，它由 G.C. Evans 创建。Evans 曾在若干场合询问过我对去伯克利有无兴趣。Evans 的兄弟曾是天津著名的西文书店的老板。我曾在那儿买过一些课本，而书价一般贵得吓人。

Evans 要退休了，我去伯克利工作的事变得认真了，确实，我有时想到，自己年纪大了，伯克利较温暖的气候很有吸引力。当然，伯克利数学系在扩展，空运的发达已使加利福尼亚不再像从前那么孤立等因素，亦促成了我的这次迁居。

伯克利一直在提高它在数学界的地位，吸引着许多优秀的学生。在我指导下有 31 名研究生获博士学位，当然我还影响其它一些学生。我开始以「第二作者身份」与年轻人合作撰写论文，如与 Bott，Griffiths、Moser，以及 Simons 等合作就是如此。在这种情况下我感觉责任较轻。生活越来越觉舒畅。

与我在学术上交往密切的同事有 Hans Lewy 和 Chuck Morrey，他们都是有创见、能力很强的分析学家。Lewy 和对 R6 中的三维黎曼度量的局部等距嵌入问题进行过一段时问的研究。它把我们导向三次渐近锥面的研究，我们弄清楚那是双曲的，但仅止于此。

数学中的微分的作用很奇妙。通常人们倾向于认为代数和拓扑是数学的两根支柱。但是事情并非那样简单；牛顿和莱布尼兹玩的是绝技。这一时期已经看到微分几何汇入了数学的主流。

老耋之年的消遣

我的生命历程正在接近终点，我唯一的考虑是怎样度过这段时光。答案很简单，我将继续摆弄数学。体育运动我从来就不在行，现在就更不用说了。听音乐对我一直是浪费时间，偶尔介入此道，纯粹出于社交之故。所幸的是整体微分几何还有许多基本问题，尽管在其发展中我很可能仅是一名观众。

我认为，研究对象限于光滑流形只是由于技术上的原因，也是不能令人满意的。不仅很自然地存在着非光滑的流形，而且即使从光滑流形开始，诸如包络这样一些几何构造也将导致非光滑流形，Whitney 引进了分层流形（Stratifiad manifold）的概念，它允许有奇点并可应用无穷小分析。

最近Robert McPherson的工作又带来了新的希望。Cheeger-Goresky-McPherson相交同调和McPherson陈类已揭示出这一概念的本质。（见2）

对我来说，Riemann结构是否像最新的进展所表明的那样基本还不清楚。毕竟Riemann在那篇历史性的论文中，允许他的度量是一种4次形式的4次根。更一般情形现在称之为Finsler度量。我在最近的一篇中指出，只要采取适当的观点，Finsler几何可以很简单地加以展开。进一步的发展则是必然的。

正如Griffiths曾注意到的，我之所以喜欢代数手法起因于我的经历。局部微分几何需要这样去作，但是要得到漂亮的局部性定理是困难的。很清楚，前面讨论过的有关最大秩的网的问题是很重要的问题，它将受到我的关注。

注：

本文原题 My Mathematical Education。译自作者于1991.10.28寄给《陈省身文选》编者的复印中。原文已刊在丘成桐主编的文集《Chern-A Great Geometer of the Twentieth Century》（1992）中。本文现收录在《陈省身──20世纪的几何大师》（《Chern-A Gre at Geometer of the Twentieth Century》中译本），交大出版社出版。

参考文献：

[1] P. Griffiths and J. Harris, Principles of Algebraic Geometry, John Wiley, 1978.
[2] Robert McPherson, Global questions in the topology of singular spaces, Proc. ICM Warszawa, vol 1, 198 213-235.
[3] J. Moser, Geometry of quadrics and spectral theory, Chern symposium, Springer-Verlag, 1979, 147-148.
[4] S. Chern, On Finsler Geometry, Comptes Rendus, Academie des Sciences, Paris (1991).

---

陈省身访谈录：数学是我唯一能做的事

Notices of AMS 返朴 2019 年 12 月 02 日 08:02

陈省身是当代最伟大的几何学家之一。他 1911 年 10 月 28 日生于中国嘉兴，2004 年 12 月 3 日逝世，明天是他逝世 15 周年的日子。下文是 1998 年刊发于《美国数学会通报》(Notices of AMS) 的陈省身访谈录，采访者杰克逊女士 (Allyn Jackson) 是该刊的资深作家和副主编。

陈省身幼年时期，正是中国兴西学，创办西方式大学学院之时，他未满 15 岁便进了南开大学学习，深深地被物理学所吸引，只是当他发现自己从事实验工作并不太顺手时，最终改为主修数学。1930 年，陈先生进清华大学研究生院，在那里，有许多已在西方社会获得了博士学位的数学家，其中中国微分几何研究的先驱者之一孙光远 (Dan Sun) 教授曾经是芝加哥大学莱恩 (E. P. Lane) 教授的学生。大约 20 年后，陈先生成了莱恩教授的继任者。1932 年，德国汉堡大学的数学家布拉施克（Wilhelm Blaschke）访问北京大学时，他的讲演给陈省身带去巨大的影响。

杰克逊：您在中国学习以后，就决定到西方来获得博士学位了？

陈省身：我是 1934 年获得奖学金由清华大学派遣来西方深造的。我 1930 年在清华做了一年助教，之后在研究生院学习了三年。我觉得对我来说去欧洲比去美国更合适，通常的情况是来美国，但是我对普林斯顿大学和哈佛大学并不感兴趣。

杰克逊：为什么？

陈省身：感觉是不太适合我的情况。我想成为一个几何学家，美国方面不具备那种我想继续从事的几何研究的条件，所以我想去欧洲。那时，尽管我是初出茅庐的学生，但是我有自己的长处，对于我想研究的、国际上的数学状况、谁是最好的数学家以及什么地方是最突出的研究中心，我都有自己的想法。我的估测可能不对，但是我有自己的思想。我决定去汉堡，事实上，后来证明这是一个非常好的选择。十九世纪末期科学的中心在德国，包括数学也是如此，而德国的数学中心是在哥廷根，还有柏林、慕尼黑也不落后。当然，巴黎始终是数学的一个中心。

我于 1934 年从清华大学毕业。1933 年希特勒在德国篡夺了政权，德国大学开展大清洗运动，逼得犹太籍教授不得不流亡国外，哥廷根从此一蹶不振，汉堡成了最好的地方。汉堡大学是第一次世界大战以后新建立的大学，不是顶出名，但是它的数学系是出色的。于是，当时我就去了那儿。

就是在汉堡大学，陈省身首次接触了嘉当的研究工作，这给先生对数学的研究方法以决定性的影响。那时汉堡大学的凯勒是嘉当思想的主要阐述者之一：凯勒已出过一本书，书中阐述的基本定理就是如今闻名的 “嘉当 — 凯勒定理” 。凯勒在汉堡大学组织了研讨班，研讨班的第一天，所有的教授如布拉施克、阿廷、赫克等都参加了。

陈省身：研讨班看上去就象庆祝会，班级里挤满了人。书也正好出版了，凯勒拿了一大堆书走了进来，每人分发一本。但是内容太难了，因此研讨班开了几次以后，就不再有人光顾参加。我想坚持到最后的就只有我一个了。我认为我能坚持到最后是由于我能紧跟其主题的缘故。不仅是那样，我当时正在写一篇有关应用其方法到另一个问题的论文。因此研讨班对我来说具有很重要的意义，我甚至去找凯勒先生。有多少次我们在一起吃饭。学院附近有一个餐馆，我们一边吃饭一边谈论各种各样的事情。我的德语是有限的，而那时凯勒先生不讲英语。不管怎么说，我们相处得很好。因此，最后我很快地完成了我的论文。

大家都知道嘉当是最伟大的微分几何学家，但是他的文章非常难懂。其中一个原因是，他用所谓的外微分。并且在我们微分几何课题中，其中你谈到了关于流形，一个困难是几何是用坐标来描述的，但是坐标没有 (内蕴) 意义，因为它们是允许进行变换的。并且为了处理这种情况，一个重要的工具是所谓张量分析或里奇演算，对数学家来说这是新的。在数学中你有一个函数，你要写下这个函数、你计算，或加，或乘，或你能微分，你有非常具体的东西。在几何中，几何位置是用数 (坐标) 描述的，但是你能任意选择你的数 (坐标) ，所以为了处理这些，你需要里奇演算。

陈省身拥有三年的奖学金资助，但是他仅花了两年的时间完成了他的学历。第三年，布拉施克安排他去巴黎和嘉当一起工作。先生不太懂法语而嘉当只说法语。第一次会面，嘉当就给先生出了两个问题要他解决。过了一段时间，他们偶尔在庞加莱研究所的楼梯上遇见，陈省身告诉嘉当他还未能解出那两个问题。嘉当让先生到他的办公室来一起讨论它们。当陈省身在嘉当办公时间准时到来时，却见这位著名数学家的办公室被许多求见者挤满了。几个月后，嘉当邀请先生到他家里与其讨论问题。

陈省身：通常在与嘉当会面后，我总能收到他的一封来信。他总是说: “自你走后，我对你的问题想得更多了…… ” 他会得出一些结果，并且也会有更多的问题，等等。他熟知所有的有关单李群，李代数的论文，而且烂熟于心。当你在街上遇见他或当某篇报告发表时，他总会抽出一些旧的信封，写上些什么，给你一个答案。为了得到相同的答案，有时甚至花费我数小时或数天的时间。大概每隔二周看到他一次。很显然，我必须努力地学习研究。这样坚持了一年，到 1937 年，我才回到了中国。

当陈省身返回中国后，成了清华大学数学系教授。残酷的日寇侵华战争限制了他与国外数学家的联系。他写信给嘉当说明了他的处境，嘉当寄了一箱他的重印本给先生，还包括一些以前的论文。先生花了大量的时间阅读和思考它们，尽管与外界隔离了，但是陈省身继续发表着他的论文，他的论文引起了国际上的注意。1943 年他得到了几何学家维布伦教授的邀请，希望他去普林斯顿学院继续深入研究。由于战争，先生花了一个星期才乘美军的军用飞机抵达美国。在学院的两年期间，先生完成了他对高维高斯 - 博内定理的内蕴证明，这把任意维闭黎曼流形的欧拉示性数表示为曲率在整个流形上的积分。这个局部几何性质和整体拓朴不变量的理论结合，在先生的工作中展示了深层的主题。

杰克逊：在您的数学研究中，您认为最重要的是什么？

陈省身：我想是纤维空间的微分几何。你知道，数学正走向两个不同的方向。一是一般的理论，例如每个人都必须学习点集拓扑学，学习一些代数学，由此打下一般的基础，那几乎覆盖整个数学的基本理论。然而也有一些课题是特殊的，而它们在应用数学上却起着重要的作用。这些东西你必须相当了解，例如一般线性群、甚至酉群。它们到处渗透，无论你是研究物理还是研究数学理论的。因此，数学中既有一般的基础理论，也有某些美妙的东西。纤维空间便是其中之一。你拥有一个空间，其纤维相当简单，这是经典空间，要把它们以某种方式放在一起。这就得到一个非常基本的概念。在纤维空间中，联络的概念极其重要，这是我研究工作的切入点。通常来说，最好的数学研究工作，是把一些理论与一些非常特殊的问题结合起来，在特殊的问题促使一般理论得以发展。我就是应用联络的思想给出了高斯 — 博内公式的第一个证明。

高斯一博内公式是最重要最基础的公式之一，不但在微分几何，而且在整个数学领域也是如此。在我 1943 年来普林斯顿之前，我就已经考虑过这一点，因此从某种意义上讲，我在普林斯顿的发展是十分自然的。到普林斯顿后，我见到韦伊，他和阿仑道弗已经发表了他们的论文。韦伊和我很快成了朋友，所以很自然地，我们讨论了高斯 - 博内公式，之后我得到了我的证明。我想这是我最好的工作之一，因为它解决了一个重要而基本的经典问题，并且思想十分新颖。为了让你的思想付诸实践，你需要有技术上的天才。这不是轻而易举的，也不是只要你有想法就可以实行的。这是微妙的。所以我认为这是件非常好的工作。

杰克逊：你最重要的工作之一是对示性类的发展。

陈省身：示性类一一它们不是给人以那么深刻的印象：示性类是非常重要的，因为这些是纤维空间基本的不变量。纤维空间是非常重要的，所以示性类产生了。不过这没伤我多少脑筋。它们经常出现，包括一阶陈示性类 c1: 因为在电磁学中你需要复线丛的观念。而复线丛引出 c1，这在狄拉克关于量子电动力学的论文中就有。当然狄拉克并没有称之为 c1。当 c1 不为零时，它是与所谓的磁单极有关。示性类的重要性是明显的，因为它们自然而然地出现在一些具体而基础的问题中。

陈省身诗 | 图源：林节玄

杰克逊：1940 年代当您首先发展陈类理论时，您是否意识到庞特里亚金的工作以及这样的事实：一个实纤维丛的庞特里亚金类可以从其复化的陈类重新得到？

陈省身：我的主要想法是，人们应该在复数情形下做拓朴和整体几体的研究。复数情形有更多的结构，而且在许多方面要比实的情形更简单。因此我引进复情形下的陈类，而实的情形要复杂得多。我读过庞特里亚金的论文，但我没有看到他的详细论文，不过我想他在英语版的《科学纪事》上发表了摘要。我是从希哲布鲁赫处得知陈类和庞特里亚金类之间的关系的。陈类可以用局部不变量曲率表达。我主要对局部性质与整体性质之间的关系感兴趣。当你研究空问的时候，你所能测量的则是局部性质。重要的是，一些局部性质与整体性质是相关联的。高斯 - 博内公式的简单情况是，三角形三个内角的总和是 180 度。它出现在非常简单的事实中。

杰克逊：您被视为整体微分几何的主要专家之一，而且您喜欢用嘉当的微分形式和联络等工具。而德国学派，如作为代表的克林根伯格，却以不同的方法研究整体几何：他们不喜欢用微分形式，他们用测地线和比较定理等手段。你是怎样看待这种差异的呢？

陈省身：没有什么根本的差异，这是传统的发展。例如，为了研究流形上的几何，标准的技巧是里奇演算。基本的问题是形式问题，这是由利普希茨和克里斯托斐耳尤其是后者解决的。而克里斯托斐耳的想法又追溯到里奇，里奇写了关于张量的里奇运算的著作。所以所有的人，包括外尔，都是通过里奇演算来学习数学的。张量分析起着那么重要的作用，于是大家都学，大家在微分几何方面都是从张量分析开始的。不管怎样，在某些方面，微分形式应该引入。我通常喜欢说，向量场就象一个男人，而微分形式就象一个女人，社会必须由两性构成。如果单有男人或单有女人，社会是不完整的。

1943 年至 1945 年，陈省身在普林斯顿研究所访问两年，之后返回中国。在中国也呆了两年，他帮助建立了中央研究院数学研究所。
1949 年他成了芝加哥大学的一名数学教授。
1960 年又至加州大学伯克利分校任教。
1979 年先生退休后依然积极活动，尤其是帮助创办了伯克利的美国国家数学研究所。
从 1981 年 — 1984 年先生出任首任所长。陈省身已培养了 41 位博士。这个数字还不包括他在频繁的访华中已有联系来往的许多学生。由于 “文化大革命”，中国失去了许多天才的数学家，数学研究的传统也几乎丧失殆尽，陈省身做了许多事情以恢复这一传统。特别是 1985 年先生对中国天津南开数学研究所的创办起到了重要作用。

杰克逊：您多长时间回中国一次？

陈省身：近年来我每年都要回中国。通常呆上一个月或更长的时间。我在南开创办了数学研究所，最重要的是拥有了一批扎根中国的杰出的青年数学工作者，这方面我们已获得了成功。我们新的研究人员包括龙以明 (动力系统) 、陈永川 (离散数学) 、张伟平 (指标理论) 、方复全 (微分拓扑) 等一批优秀的年轻人。我认为在中国对于数学研究最大的障碍主要是报酬太低。顺便说一下，国际数学联盟已将下一届国际数学家大会选定在北京举行。

杰克逊：你认为中国在数学方面会有极大的提高吗？

陈省身：嗯，是的。我所担忧的，倒是中国将会有太多的数学家了。

杰克逊：中国是一个大国，可能他们需要大量的数学家。

陈省身：我认为他们不需要太多的数学家。中国是一个大国，自然她有许多人才，特别是在一些小地方。举个例子，有国际性的中学生奥林匹克数学竞赛，中国学生表现都是十分出色的。不过象这种情况，为了赢得竞赛，这些学生需要培训，结果其它课题就被忽视了。在中国，父母们总想让他们的孩子学英语，做生意，赚更多的钱。而竞赛是不给钱的。我想，如果哪一年这种培训方面他们投人得少了，中国的成绩就可能立刻下跌。

1943 年当先生选择去德国攻读研究生时，在美国，几何学还只是一个刚刚起步的领域；到 1979 年他退休时，几何已经成为最辉煌的方向之一。这种变化多半归功于陈省身。然而，陈省身对他的成就却极为谦虚。

陈省身：我不认为我高瞻远瞩。我只是在做一些小问题。数学中涌现出许多概念和新思想，你只是提出一些问题，然后尽力得到简单的答案，并期望给出简单的证明。

杰克逊：那就是说，你先观察，然后产生想法？

陈省身：对。在大多数情况下，你什么想法也没有。而在许多情况下，你的想法也行不通。

杰克逊：您把自己描述为一个解题者，而不是理论创立者？

陈省身：我认为这种差异是很小的。每一个好的数学家都应该是一个解题者。不然你仅有模糊的想法，如何能作出杰出的贡献？你解决了某些问题，你用某些概念，至于数学贡献的评判，可能要到将来才能看到。

要评估一个数学家或数学的某个方面是很困难的。如可微性的概念。二三十年以前，许多人不喜欢可微性。许多人对我说: “ 我对任何带有可微性概念的数学一概不感兴趣。” 这些人想使数学变得简单。如果拒绝接纳涉及到可微性的思想，你就排除了许多数学。这就不够了，牛顿、莱布尼茨应该发挥其作用。不过这是有趣的，因为在数学中有许多有争议的想法。

杰克逊：你可以举几个引起争议的例子吗？

陈省身：一件事是当今一些论文太长了。如 “ 有限单群” 的分类，谁打算去阅读 1000 多页的证明？或还有四色问题的证明。我想人们必须使数学有趣些。

我认为数学不会很快消亡。在一段时间里它到处存在，因为它还有许多美妙的事情要做。研究数学是个人的行为。我不相信可以由一群人来做数学，基本上这是一种个人行为，从而也容易做。数学不需要太多的设备，它不象其他科学，它们比起数学来需要更多的物质设备。所以数学可以延续一段时间。我不知道人类文明能持续多长时间，比起数学来，那是一个大得多的问题。但是就数学本身，我们还要与它相处一段时间。

86 岁高龄的先生继续还在从事数学的研究。近年来他一直对芬斯勒几何尤感兴趣。两年前他曾在本刊上讨论过这一点 ( “ 芬斯勒几何就是无二次型限制的黎曼几何” 19 9 6 年 9 月，9 5 9— 9 6 3 页) 。

陈省身：芬斯勒几何比起黎曼几何要来得广泛得多，而且能用统一的方法进行处理。它将是大学未来十年里微分几何基本课程里的内容。

在数学上我没有什么困难，所以我当我做数学时，我是在欣赏它。我之所以一直在做数学研究，也是因为其他事情我做不了。我已经退休多年了，还有人问我是否仍在研究数学。我想我的答复是：这是我能做的唯一一件事，没有其他我能做的事。我一生都是这样。

此文根据《苏州教育学院学报》上的译稿《当代最伟大的几何学家陈省身先生访谈录》修订编辑。

---

陈省身访谈录：科学上最伟大的发现都不是有计划的

田淼 返朴 2023 年 05 月 23 日 08:01 上海

本文基于作者 1999 年 12 月至 2000 年 2 月间对陈省身先生做的三次采访，主要囊括三部分内容：陈省身谈布尔巴基学派、谈纯粹数学与应用数学的关系以及中国数学的人才培养与发展。这几次交流为当时提供了许多新史料，也显现了这位伟大数学家睿智、坦诚的观点。

撰文 | 田淼 (中国科学院自然科学史研究所)

来源 |《中国科技史料》2000 年第 21 卷第 2 期

陈省身，1911 年 10 月 28 日生于浙江嘉兴 1。他于 1919 年秋天上过一天初等小学，次年考入秀州高级小学。1922 年秋，随全家至天津，并于当年冬入扶轮中学读书。1926 年中学毕业，考入南开大学。因不喜做实验，于二年级分系时入数学系，随姜立夫 (1890～1978 年) 学习 2 [1]。1930 年，陈省身大学毕业，考入清华大学数学系随孙光远 (1900～1979 年) 3 攻读硕士学位，成为中国自己培养的最早的数学硕士研究生 4。1932 年起，陈省身开始于《清华大学理科报告》及《东北数学杂志》(日本) 发表射影微分几何方面的论文。1934 年，他获得理学硕士学位。

1934 年，陈省身得到清华大学的留学资助，在他的要求下，获准赴德国汉堡大学数学系随布拉施克 (W. Blaschke，1885～1962) 教授攻读博士学位。赴德后不久，他即发现并弥补了布拉施克论文的一个漏洞，在《汉堡大学数学讨论会论文集》第 2 集发表论文《关于网的计算》，得到了布拉施克的欣赏。在德国期间，他随凯勒 (E. Kähler，1906～) 学习了埃里・嘉当 (É. Cartan，1869～1951) 的理论。1936 年 2 月，陈省身获得博士学位。同年 9 月，赴巴黎随埃里・嘉当做博士后研究。从此确定了他一生的研究方向：大范围微分几何。[2]

1937 年夏，陈省身回国，任西南联合大学数学系教授。他在西南联大工作了 6 年 (1937～1943 年)，开了 “李群”、“圆球几何学”、“外微分方程” 等课程。王宪钟、严志达、吴光磊及物理学家杨振宁等都于此听过陈省身的课。1943 年 7 月～1945 年，陈省身赴普林斯顿高等研究所工作。此间，他完成了两项划时代的工作。一为黎曼流形的高斯 - 博内公式的内蕴证明。这一工作得到了韦依 (A. Weil，1906～1998；法国数学家) 的欣赏，他们遂成为好友 [1，3]。一为埃尔米特流形的示性类论。在这两项工作中，他首创应用纤维丛概念于微分几何的研究，引进了后来通称的陈示性类，为大范围微分几何提供了不可缺少的工具，开复流形的微分几何与拓扑研究之先河 5。

1946～1948 年，陈省身受姜立夫先生的推荐及委托，任中央研究院数学研究所代理所长。他选拔了一批出色的青年数学家作为助理研究员，其中包括吴文俊、陈杰、陈国才、周毓麟、叶彦谦、张素诚、廖山涛、杨忠道等重要的数学家。陈省身为他们开设代数拓扑课。[4]

1948 年 12 月，陈省身举家赴美，1949 年 1 月抵达普林斯顿高等研究所。1949 年，他至芝加哥大学数学系任教授，在此任教 11 年，指导了 10 个杰出的博士生，其中包括中国数学家廖山涛 6。1960 年，陈至加州大学任教，在此，有 31 人随他完成了博士论文，其中包括梁树培、黎翰飞、丘成桐、郑绍远、宋枕寒、李伟光、王蔼农等 8 位华人数学家。1981 年，美国政府决定于伯克利建立数学研究所。陈省身成为首任所长。1984 年退休。其间，他又做出多项重要工作，并培养出一批出色的数学家。[5]

1985 年，陈省身在母校天津南开大学创办并主持了南开大学数学研究所，致力于在 21 世纪将中国建成数学强国的伟大事业。1992 年，他辞去所长的职位，但仍旧担任该所名誉所长。

陈省身在其著作中引进的一些概念、方法与工具，其影响已远远超出微分几何与拓扑学的范围，而成为整个现代数学中的重要组成部分。由于其对数学的重要贡献，陈省身享有多种荣誉。1961 年，他当选为美国科学院院士；1994 年 6 月，他当选为中国科学院首批外籍院士。他还先后获得美国数学协会的肖夫内奖 (1970 年)、美国总统颁发的美国国家科学奖 (1975 年)、美国数学会斯蒂尔奖 (1983 年)，及国际性的沃尔夫奖 (1984 年) 等等。作为公认的世界数学大师，陈省身的成就及生平早已成为中国数学史界乃至国际数学史界的重要研究课题，并已有多篇相关文章发表 [3，5~8]，故本文于此只作上述简要叙述。

笔者有幸于 1999 年 12 月 28 日 9 时至 12 时、2000 年 1 月 3 日 9 时 30 分至 12 时 30 分和 2000 年 2 月 19 日 9 时 30 分至 12 时在南开大学数学研究所对陈省身先生进行 3 次采访 (图 1)。现将采访中所得之部分新史料汇成此采访录，于中国现代数学史之研究或不无小补。

01 陈省身谈布尔巴基学派

1936 年 9 月陈省身赴巴黎随埃里・嘉当学习。此间，布尔巴基学派恰在巴黎开设题为 “嘉当的数学工作” 的讨论班。作为一名普通学生，陈省身参加了这一讨论班。他对这一段经历的回忆及对布尔巴基学派工作的评价是数学史上的珍贵史料。

田淼(以下简称” 田”)：1936 年至 1937 年间，布尔巴基学派的讨论专题是埃里・嘉当的工作。

陈省身(以下简称” 陈”)：对的。

田：您是否参加了他们的讨论？

陈：我去了他们的讨论班。

田：那时他们的集会还是在 Capaulad 咖啡馆？

陈：不，那时是一个正式的讨论班。题目是埃里・嘉当的数学工作。每两个星期聚会一次。是在讲堂里，完全是一种正式的 Seminar 形式。

田：是否任何人都可以参加呢？

陈：任何人都可以去。

田：他们关于嘉当工作的认识与您对他的工作的认识是不是一致的呢？

陈：差不多一致。因为埃里・嘉当做过很多工作，这些工作不是几次报告就可以讲清楚的，所以整整讲了一年。一年间，每两星期一次，把他的工作分成段，由不同的人来讲。这个工作的笔记后来都出版了。

田：既然是讨论班，应该是所有的与会者都可以发言吧？

陈：是的。

田：那么这个笔记中有没有您的贡献呢？

陈：没有。

田：有的数学史家认为布尔巴基学派反对应用数学，有这个问题吗？后人对这个学派有很多批评，您是如何看待这些批评的呢？

陈：这其实没有。要讲这个问题，首先要了解布尔巴基学派的背景。20 世纪初，世界上，尤其是德国兴起了许多新的数学分支，如拓扑学及抽象代数。但当时法国的数学领袖，也就是当年巴黎几个大学的数学教授，他们虽然都是很伟大的数学家，却不太注意当时的数学发展，对于这些新兴的学科多数不接头。法国数学家多半是重分析的，像毕卡 (É. Picard, 1856-1941；笔者注，下同) 、阿达玛 (J. Hadamard，1865～1963) 等等。当然庞加莱 (H. Poincare，1854～1912) 是很博学的，现代数学的许多分支都起源于他的工作。布尔巴基的成员大多是法国高等师范学校的学生，他们不满于老教授们不顾当时数学进展的教学方式，所以他们决定自己来做，自己讨论 7。

以我的意见，后人对于这个学派的批评不一定很合理。因为他们要念数学，要念当时正在发展的数学。同时，他们也认为，当时的数学发展太多了，有的发展不是很可靠，比如有的定理证明不完全。所以，他们想把当时的整个数学重写一遍，而且他们书里的定理都要有严格、准确的证明。这样他们的范围就不能太广，因此他们的工作集中于纯粹数学，而没有顾到应用数学。

实际上，他们的工作并没有做完。可是这部书的影响很大，因为它是对近代数学的总结，所以人们都会读它。有许多人不知道它的背景，只读这部书，所以会批评它。诸如它忽略了应用数学等等。实际上，他们不是不想做，只是限于时间、能力，所以只限于当时的纯粹数学。

田：您和许多布尔巴基学派的成员都是朋友，当时您和他们是不是有很多交往呢？

陈：不太多。我和他们的交往多半是在我去美国以后。Claude Chevalley (谢瓦莱，1909～1984；法国数学家) 是普林斯顿的教授，我和他很熟。我和 A. Weil 认识也是在去美国之后。当时他住得不远，我们的工作比较接近。他喜欢交朋友，我们又谈得来，所以就成了很好的朋友。亨利・嘉当 (H. Cartan，1904～) 是埃里・嘉当的儿子，在巴黎时，我们认识，不过没有很多交往，只是和 Ehresmann (C. 埃瑞斯曼，法国数学家) 的交往多一点。总之在巴黎的时候，我和布尔巴基成员的来往不多。

因为我那时还是一个普通的学生。你要和这些人有些来往，你自己必须也要有一些成就和一定的地位，见了面要有话说。否则，也是浪费他们的时间。后来我和布尔巴基的人，比如 Dieudonne (J. 迪厄多内，1906~1992) ，Godement (古德曼) 等等他们都很熟，来往也很多了，因为我做了一些有意义的工作，这样交往起来就容易了。

02 陈省身谈纯粹数学与应用数学

陈省身在微分几何方面的工作对于整个数学的发展都起到了很大的促进作用，同时在理论物理上也有很大应用。关于数学的应用，陈先生如是说：“数学是可以有应用的，这是很奇妙的。这种应用性，最初不能想象，现在非常要紧。许多东西，数学都能跑进去，纯粹数学和应用数学根本是一片，不能划线划在什么地方。”

田：您在 1946 年发表的文章中给出了陈示性类。吴文俊先生说在各种示性类中您的这个示性类是最基本、最有应用前途的一个 [9]。

陈：最有应用的，最简单的。

田：当时您在做的时候有没有考虑到它的应用性呢？

陈：主要是有一个数学的情况，你想要了解它，所以就要设法回答这个情况所引起的一些问题。当时根本就不会考虑它会有多少应用，也无法考虑。

田：您的工作是把实数空间的数学结果推广到了复平面。

陈：是的，主要的是空间的观念改变了，扩大了。最初的几何学是欧几里得几何，后来也有非欧几何，及其它的几何学。在黎曼 (G.F.B.Riemann，1826～1866) 他们的工作之后，有流形的观念。这是一个很困难的概念，因为什么叫做流形，怎样处理流形，怎样解决流形的问题，是这一百多年来重要的和主流的研究课题。刚巧我做的这个问题在这里是一个非常基本的观念，示性类是其中一部分比较具体的贡献。

田：它应该属于数学内部的发展。

陈：是数学的发展，在物理上也有应用。非常奇怪的，整个的示性类内容在物理上有应用，并且是物理上一个很基本的问题。电磁学，是物理上一个很要紧的观念。所有的近代科学都是靠电磁学发展起来的，电磁学的基本方程是麦克斯韦方程，而麦克斯韦方程的数学基础就是纤维丛的观念，其中就用到了我的示性类。实在是巧极了。这么一个简单的数学观念，当然也不是很简单了，其中有一点弯曲，到处都用得到。由于我们对于空间的观念扩大了，所以要对这个扩大的空间有所了解。在这个了解中的一个关键就是我的示性类。因此它重要。有的时候也是时机合适，有的时候就是运气。

田：好像在最近，理论物理和数学的联系越来越紧密，比如说，一些大的数学家，比如说像您，您的理论在理论物理上就很有作用。

陈：陈示性类，尤其是陈 - Simons 不变式都广有应用。

田：而杨振宁先生的成就对数学也起到了很大作用。

陈：它在微分拓扑方面引导了最重要的发展。

田：从以前的观念来看，数学是一切科学的基础，所以应该是其它专业的科学家来学习数学。但现在，好像数学家也开始重视其它科学的研究，甚至主动关心他们需要什么样的数学。比如像外尔 (H. Weyl)、范・德・瓦尔登 (van der Waerden，1903～1996)，他们写过微分方法在理论物理中的应用方面的书和论文，而布尔巴基学派也邀请物理学家去参加他们的聚会，去讲明物理学家需要什么样的数学。那么理论物理在现在数学的发展过程中究竟起到一个什么样的作用？

陈：非常要紧。学问是一个广得不得了的，散得不得了的，可是很奇怪的，有一部分学问加在一起是一个整体。比如说牛顿 (I. Newton，1642～1727)，牛顿了解力学的性质，有他的基本定理。那么数学家就要搞这套东西，一个很重要的人是拉格郎日 (J. L. La-grange，1736～1813)。拉格郎日写了一本力学的书，主要内容是关于牛顿的万有引力。这方面最简单的应用是，两个物体在万有引力的作用下，一个绕着另一个转，成一个椭圆。那么物体多了怎么办？在引力作用之下，世界上这么多的物体，会不会有一天垮掉了，碰撞了，或者互相炸掉了等等。于是就要证明世界是稳定的。数学家要证明这样的一个大问题，当然这是很难的，因为物体太多了，非常复杂。麦克斯韦方程之所以重要，是基于电的重要性，电力比普通的力要强得多，所以在近代的文化发展上起了很大的作用。电的基础是麦克斯韦方程，当时是很不得了的成就。法拉第认为麦克斯韦方程可以写成一个方程。而一维纤维的几何表示正是麦克斯韦方程。麦克斯韦方程是一个一维的方程，这个方程写下来只有一个方程，但是它是一个外微分方程。把它展开来，成为一组偏微分方程。其中每个方程都有几何意义，也都有物理意义。当年法拉第的实验证明了麦克斯韦方程，这就相当于把法拉第的实验完全用数学形象了。麦克斯韦方程只是一维空间的，到二维就是杨 - Mills 方程，所以杨振宁的这个发现是不得了的。现在国内大家还不很了解，因为他的方程要比麦克斯韦方程复杂得多。我们搞的纤维丛方程、麦克斯韦方程、杨 - Mills 方程，这种数学的方程可以变成物理现象，在物理实验中看得出来的。不但看得出来，连数量都可以对。这实在是很有意思的。数学和物理加在一起的发展是不得了的。其中一个很重要的情况就是要把数学的观念量子化。因为是做到更小的东西的时候，它的力量就更大，所以这个作用就大得很。这也带动了数学的发展。

田：这个方向是有了物理现象去找它的数学根据呢，还是数学家主动地去找自己数学方程的物理意义呢？

陈：**科学上最伟大的发现都不是有计划的。**现在大家写研究计划，这些计划的对象都不是第一流的研究工作。

陈：北京的九所请我做了个报告，我也许要把它写下来，这个演讲题目是几何和物理。最简单的，牛顿的方程 F=ma，你把 m 写到这边来，F 除以 m 等于 a，F、m 是力和质量，是物理，右边的是加速度，是几何。物理等于几何。

田：我最早学加速度的概念还是从物理里学的。但是您现在说它是一个几何概念。您是从什么角度来说这个问题的呢？

陈：这是二阶微分的概念，在几何上叫做曲率。

陈：爱因斯坦方程也是一样，爱因斯坦说我们的世界、宇宙是一个四维空间，四维空间有一个 ricci 曲率等于 stress tenser (应力张量)，这是爱因斯坦方程。Ricci 曲率是几何，而 stress tenser 是物理。麦克斯韦方程也是一样。我要把它写下来，也是一样的。一个几何的量等于物理的量。

田：那么关于数学和应用数学，您是怎么看的？

陈：数学是可以有应用的，这是很奇妙的。这种应用性，最初不能想象，现在非常要紧。许多东西，数学都能跑进去，纯粹数学和应用数学根本是一片，不能划线划在什么地方。

田：是不是可以说，真正一流的，也就是最出色的数学成果也许会成为一种最出色的应用数学，但实际上在其研究的过程中往往并不会考虑到应用的问题。如果只是为了应用去做一个问题，也许它并不具有远大的应用前景。

陈：这当然。这种问题是很微妙的。比如说，我做的陈示性类的工作是一项纯粹数学工作。最近，陈永川告诉我说，“陈 - 西蒙斯” 的名字，在 SCI. 的索引上，光标题里引用的，而不是只在文章里引到的，就有一千多次。应用数学哪里有这么重要的贡献？没有的。

03 陈省身与中国数学

陈省身于 1937 年归国，先后在长沙临时大学、西南联合大学执教。1946～1948 年 12 月，受姜立夫先生的推荐和委托，他任中央研究院数学所代理所长。这期间他除了自己做了很多研究工作以外，还为我国培养了一些出色的数学人才。

田：在西南联大期间，您主要是讲解基础性知识呢，还是比较高深的知识？

陈：我不大分的。

田：当时的学生能够接受吗？

陈：西南联大有一个好处，我们有很好的学生。

田：也就是说总有好学生能够跟上您的课程。那么差的学生呢？是不是就去掉了？

陈：他们也学了一些东西 8。

田：您对您在西南联大培养的学生有什么样的评价？

陈：王宪忠，很好的数学家，严志达是院士，吴光磊，后来在北大。我比较喜欢私人的交往，所以和学生们的关系都很亲密，常常来往。不过我不喜欢有些官方的东西。比如说中央研究院成立数学所我们不开会，没有挂牌子，也没请几个要人之类的来参加讲几句话，我不搞这一套。我们还是做同样的事情。[10]

田：清华复校以后，您是否和清华大学脱离了关系？

陈：不是，而且在 1947 年春天的第二个学期我还在清华上了一个学期的课，还是清华的教授。那时在复原的时候，他们一度要我做代理系主任。因为当时杨武之是系主任，他在昆明没有回北京，所以他们叫我做代理系主任。我没做，因为我那时候也没有回北京。

田：1946 年，您受姜立夫先生之托任中央研究院数学研究所的代所长，当时您对中国数学的发展，特别是这个研究所未来的方向是不是有一些设想？

陈：希尔伯特 (D. Hilbert，1862～1943；德国数学家) 说过，数学是大数学家的工作。我也认为，研究数学最重要的是要有好的数学家，所以最主要的是找人，培养人。人们总要讲研究方向、教育计划，这个计划最没有道理。计划有什么用呢？要做，要深入地做下去，最重要的是要有人。 最近，周光召院长 (时任科协主席) 也在说中国科学的发展需要人。我当时只是想替中国培养人才。所以我找了一群年青人到数学所来。当然我们要有工作做，所以就搞拓扑，选了这么个题目。

田：您在西南联大和中央研究院数学所好像主要是致力于培养拓扑和抽象代数方面的人才。

陈：各方面都有。实际上我对数学方面的兴趣是非常广的。表面上讲我学几何，不过几何需要分析，需要拓扑等等。我对于数学各方面都有兴趣，只要需要的时候我就会看一看，懂一点。

田：吴文俊先生说他只跟您学了一年就开始在拓扑方面出成果了。

陈：那是件很不得了的事情。

田：吴先生现在也是大数学家 [11]。

陈：是的，很大。吴文俊在一年后不光开始做工作，他的论文发表在 Ann. of Math. 上，这是全世界最要紧的、水平最高的数学杂志。他的问题是当时的拓扑学家惠特尼 (H.Whitney) 认为非常难的问题。惠特尼也是我的朋友。他当时关于这个定理的证明简直是一本书，吴文俊十几页就证出来了，9 很不得了，很重要的工作。

田：当时您开拓扑课应该是在为这些青年研究人员打基础？

陈：当然。

田：那么后来您为什么在一年之后停止了，而没有开新的课？

陈：后来么，当时的政府垮掉了。结果我到美国去了，所以没有什么选择的问题。

田：中央研究院的数学所可以说是您一手创办的，您能否谈一下它对后来中国数学发展的影响？

陈：我们有一大群很好的年青人，数学学生。他们在那里念书，后来他们很多人都是很成功的。最有名的，比如说在国内的，有吴文俊，有廖山涛，国外有陈国才。陈国才的工作是很好的，在国际的水平都是非常好的。周毓麟，他现在在九所，孙以丰等等，十几个人。10

田：国内对陈国才的介绍很少。

陈：他是个不得了的人。他不只是在国内没有太大的名气，在国外名气也不很大。现在他死了，人们才开始注意他的工作。现在巴黎等等地方都在讲他的工作。

田：您认为从数学研究的角度上来讲，数学研究所和大学数学系比起来有一些什么样的优势？

陈：我想很有优势。如果一个大学毕业生到大学去做助教，他需要教书，因此花在念书上的时间就会少一点。在数学研究所他可以念比较深的数学，用在数学上的时间多一些，并且也比较有指导。

田：也就是可以有大的数学家做指导。

陈：是的。

田：您在发现一个人的数学才能方面很有特长。比如说周炜良先生，您认为他有很强的能力，而他确实是非常出色。还有，比如吴文俊先生，您只和他谈了几次话就决定吸收他入中研院数学所，您是不是很快就发现吴先生的数学才能。

陈：是的。我想主要是看他的反应，看他反应快不快。比方说学一门新课，你拿本教科书看看，一下子就懂了，那么你的反应就快了。你快了，你就吸收得多，就有可能可以做一些东西，可以有所贡献，而太慢了就跟不上了。我看一个人的能力就看他的反应，你说了一个内容，如果他只能听或者只能记，这就没有反应出来。我想对于一个人，你是不是应该搞数学，是不是应该拿数学作为终生的职业，主要的是你的数学才能好不好。哈代说，一个决定性的因素是你是不是比老师好。如果在上课时，你对课程的了解不亚于你的老师，那你就可以念数学。如果往往他讲了很多内容，你都不大清楚，还要回去再看，这就差了。我想，是否该学数学，还是要看你的数学本领如何。但你如何判定自己的数学才能，究竟是不好，是中等，还是在什么位置，要有你自己的一个标准。

田：您有没有这样的学生，在他学到一半时，您发现他没有数学才能？

陈：当然有。

田：这时您怎么办呢？是不是劝他放弃数学？

陈：他当然有别的才能可以发展，天无弃材！

田：您在国内时，不仅自己做研究，培养学生，还对其他数学家有很大影响。据周炜良先生说，是您劝他重回数学研究的。

陈：不可以完全这么说。实际上，虽然我们是好朋友，但我也不能劝。因为从他的未来来考虑，究竟是不是做数学好，当时并不明显。他回国后，在中央大学做了一年教授，薪水相当高，过得可以。后来中央大学搬迁，他当时家在上海，所以他就去上海了。那时是战争的时期，生活也很困难，不稳定。等到战争结束后，他开始做生意，赚了些钱。所以那时他正处在一个十字路口，究竟该如何走，我不敢说，是他自己的决定。当然，当时他自己也不很清楚，究竟是该继续做生意呢，还是回到数学。我想，如果他要继续做生意，他也会是成功的，他是一个很能干的人。所以我也不能劝他。虽然他后来的文章里很感谢我对于他的影响。当时，我的立场就是，他如果决定要做数学，我可以给他帮忙，我可以介绍他和数学家来往以便获取相关的资料。因为我认识很多数学家，我是一个跟人来往很多的数学家，不是关了门念书的那种人，所以这方面我可以帮他忙。不过是不是回到数学研究中来，是他的决定，我不应该影响他。他重回数学研究之后很成功，做了好几项要紧的工作。

田：周先生说对他做决定起到很大作用的是您给他提供的 Zariski (O. 扎里斯基，1899～1986) 的文章 11。

陈：对。因为我有这些单印本。Zariski 我也认识，他的有些单印本我也带回来了，我交给周炜良，他念了这些文章。[12]

田：您回国后，经常提到抽象代数和拓扑学是现代数学研究的基础，这在当时的中国数学界是否有共识？

陈：不敢说有。当权者喜欢讲应用数学，虽然他们实际上并不知道应用数学是什么。

**田：**除了自己做研究和培养学生之外，您还发表了一些科普性质的文章，如您在 1947 年第 3 期《科学》上就发表过一篇《什么是拓扑学》，后面还列了一些入门书籍。您对科普工作是怎么看的？您觉得大科学家是不是也该做一些科普工作？

陈：科普自然是一门大学问。人人都该对科学有兴趣，惊叹它的发展。每个科学家都有责任把他的工作解释给朋友。

田：您在美国还培养了一些中国学生，如廖山涛、丘成桐等等，您可否谈一下他们的情况？

陈：都是一流的数学家。

田：除廖山涛以外，其他学生是否也有回国的呢？

陈：有的，暂不举名。他们都有相当的水平。

田：您是不是也劝他们回国呢？

陈：是的。比如说陈永川就很难得。他当年在美国毕业的时候是第一名，是很容易在美国找到工作的，但他决定回来。

田：您认为近来影响中国数学发展的最大因素是什么？

陈：我想最主要的因素是待遇太差。中国有不少很好的数学家长期在国外。并不是每一个人都能成为大数学家。中国是一个很大的民族，但他能够产生的数学家有限，结果很大一部分给出口了，他自己就少了。我想现在政府慢慢加一点力量，支持得多一些，情况可以改善一些。

田：您捐出三分之一的财产来创立 “陈省身基金”，是不是就是为了从这方面为中国数学做些工作？

陈：我有两个孩子，现在我把南开数学所作为第三个孩子。我多年积蓄，存了一些钱，对我已经无用了。

田：您对南开数学所采取什么样的管理模式？

陈：我不管的。我来了之后，有一些活动。比如说，我们有津京几何工作营，在 99 年 10 月份开过一次，2000 年 3 月 6 号还要开，规模比较大，很多人都要来。下个星期一、二 (2000 年 2 月 22、23 日)，萧荫堂来讲座。他可能是当今世界搞复变函数最出色的数学家。这样搞一些活动，慢慢来。同时，我们还在搞试点班，我们的试点班有很好的学生，我要训练他们。这些学生都是本科生，我希望每年能培养四、五个很好的学生。

田：这些学生能够跟得上您讲的课程吗？

陈：一部分好的学生可以跟得上。

田：南开数学所的人员是固定的吗？

陈：有固定的人员。不过我们的人员很少。他们都很出色，如果在国外，都可以在最好的大学做教授。他们长期在南开，不像其它学校请的专家，只是短期讲学，那样不能起到太大的作用。当然，我也鼓励他们出去开会，交流，必须要保持和国外的联系。以后我还要请一些人，要把这里建成一个国内的数学基地。

田：这就是您对南开数学所未来的期望？

陈：希望有不少人从南开得益。我不喜欢讲空话。

田：您在谈到要将中国建成 21 世纪的数学大国这个问题时，您的主要依据是什么？

陈：从物质上来说，研究数学不需要太多的投入，有了传真，可以将我们和全世界联系起来，能够拿到必要的材料。另外，从历史上可以看出，中国人的数学才能是不容怀疑的。1900 年时，我们中国的现代数学还没有起步，现在，全世界的华人中出了很多重要的数学家。一百年以后，中国的数学应该是很像样的了。

2000 年 1 月 13 日，陈省身先生的夫人郑士宁女士不幸去世。1939 年 7 月陈省身与郑女士在昆明结婚。1999 年 12 月 28 日，笔者第一次采访陈先生，做了两个多小时的谈话。陈夫人特别派人提醒陈先生注意时间。当时，陈先生说：“现在我的一切都由我太太安排，她担心我的身体”。语音犹在，而陈夫人竟已作古。2000 年 2 月 19 日，陈先生说：“我们结婚 60 年，这 60 年间，发生了很多事情”。这简单的话语中所包含的对陈夫人的深情与思念，令笔者一时语塞。

如今，89 岁高龄的陈省身先生仍然继续其数学研究，并为 21 世纪将中国建设为世界数学强国的目标而辛勤劳作。现谨以此文表达我对陈夫人的深切哀悼及对陈先生的无限敬仰。

致 谢郭书春研究员与袁向东研究员对本人的采访给予了很多具体的指导和建设性的意见，张洪光教授提供了有关陈省身先生的文章等资料，艾素珍女士也提供了很多宝贵意见。在此谨致谢意。

作者简介：田淼 (1967 一)，天津人，中国科学院自然科学史研究所研究员。

注释

1、陈省身在其《学算四十年》(陈省身文选。北京：科学出版社，1991.26～36)、《学算六十年》(陈省身文选。北京：科学出版社，1991.37～47)、《我的科学生涯与著作梗概》(陈省身文选。北京：科学出版社，1999.59～76) 等文章中均称其生于 1911 年 10 月 26 日。后经张洪光考证 (陈省身 ——20 世纪伟大的几何学家。科学巨星 —— 世界著名科学家评传 (I). 西安：陕西人民出版社，1995) 证明其生于 1911 年 10 月 28 日。陈省身在接受本人采访时证实了张洪光的说法，并指出，由于阴阳历日期换算之误造成了前一日期的不准确。本文采用张说。

2、姜立夫，专攻几何学，是现代数学在中国最早而又最富成效的一位播种人。详见：吴大任。姜立夫。中国现代数学家传・第一卷。南京：江苏教育出版社，1994.17～34。陈省身曾随姜氏学习复变函数、高等代数、微分几何、非欧几何等课程。

3、孙光远，专攻射影微分几何，是我国研究微分几何与数理逻辑的先行者。详见：钟瑚锦，孙钟秀。孙光远。中国现代数学家传・第二卷。南京：江苏教育出版社，1995.70～75。

4、由于清华大学推迟一年办研究院，陈省身与吴大任于 1931 年开始其研究生学习，1931-1932 年间，陈省身任清华大学数学系助教。吴大任因赴南开大学任助教，未能完成研究生课程。在采访过程中，陈先生指出：“那时是中国最初办研究院，我想我是最早的。”

5、2000 年 1 月 3 日，陈省身在接受笔者采访时说：“我最好的工作是在那儿 (普林斯顿) 做的。” 即是指此两项工作。

6、廖山涛 (1920~)，1938～1942 年间在西南联合大学学习，50 年代留学芝加哥大学研究生院，在陈省身的指导下完成博士论文《关于纤维丛障碍的理论》，并获得博士学位。1956 年回国，任教于北京大学。他在代数拓扑及微分动力系统的研究方面有出色成就。由于在微分动力系统方面的成就，1982 年和 1987 年先后获得国家自然科学奖二等奖和一等奖。1986 年，又获得第三世界科学院首次颁发的数学奖。详见：丁同仁。廖山涛。中国现代科学家传记・第二集。北京：科学出版社，1997.112～119。

7、陈省身指出：“法国高等师范学校的学生非常出色。他们经过严格的筛选，并由政府供给他们的生活与学习，所以都很优秀。”

8、陈省身在《联大六年 (1937-1943》(陈省身文选。北京：科学出版社，1991.12～13) 中回忆，“联大数学系主任先后由江泽涵、杨武之先生担任，三校联合，教员不缺，所以我有机会开高深的课，如‘李群’，‘圆球几何学’，‘外微分方程’等。我也曾同华罗庚先生、王竹溪先生合开‘李群’讨论班”。

9、1948 年，吴文俊在普林斯顿《数学年刊》第 49 卷第 2 期上发表了论文 On the Products of Sphere Bundles andthe Duality Theorem Modulo Two, 大大简化了惠特尼 (H. Whitney) 对其示性类的一个重要的对偶定理的证明。陈省身对此十分欣赏，该文就是由陈推荐发表于《数学年刊》上的。见文献 [10]。吴文俊回忆这一工作时称：“我在国外访问期间，曾与国际友人谈起个人的学术经历。我说起我与陈师本不相识，只是在中央研究院数学研究所待了一年，从陈师学习代数拓扑，从此走上了拓扑的研究道路。闻者大为惊异，拓扑号称难学，一年就在拓扑上做出研究成果，认为不可思议，因而见人就说此事。其实这并不可怪，这正好说明陈师善于提携后进，指导有方所致。如此而已。”([9]，v)

10、陈省身在其 (中央研究院三年)(陈省身文选。北京：科学出版社，1991.16～19) 一文中对于中央研究院数学研究所初建的情况及其中的研究人员做了较为详细的介绍。最早在我国开设拓扑课程的江泽涵先生对陈省身此一工作的评价为：“对于使拓扑在国内生根，陈的这三年工作已经确实作出了空前的贡献。”

11、周炜良曾如此描述陈省身对其重回数学研究的影响：“在战后中国的那种条件下，陈意识到中国数学家最迫切需要的是他们各自研究领域的最新文献。为此陈收集了大量的预印本，其中不仅有他自己研究领域里的数学家的，也有相关领域的数学家的。对我来说，我很高兴在他收集的预印本中发现 Oscar Zariski 的大多数最新论文。…… 陈也对我说起 Andre Weil 的重要工作，…… 那时我很清楚，如果我想重新研究数学，首要任务是研读陈很友好地借给我的 Zariski 的论文。陈还建议我到 Princeton 的高等研究院去待一年，以便了解当代数学的主流。…… 我觉得，尽管我损失了过去十年，但我重新研究数学还不是太迟。实际上，陈甚至给 Lefschetz 写了一封信，建议他邀请我访问 Princeton。”“很显然我得做一个重要抉择，或许这是我一生中最关键的选择，是否离开生意场而重返数学界。毕竟我已经 35 岁了，我获得博士学位已经是十年前的事了，而且自那以后我几乎没有接触过数学。看起来我已经不大可能做一个数学家了，这种处境使我如此沮丧以至于我打算放弃数学。但是，与陈的谈话改变了我的想法，使我又看到了继续研究数学的希望。”[12]

参考文献

[1] 陈省身.学算六十年[A].陈省身文选[M].北京：科学出版社，1991.37-47.

[2] 陈省身.我同布拉施克、嘉当、韦尔三位大师的关系[A].陈省身文选[M].北京：科学出版社，1991.20-22.

[3] A.韦依.我的朋友——几何学家陈省身[A].陈省身文选[M].北京：科学出版社，1991.XI-XVI.

[4] 陈省身.中央研究院三年[A].陈省身文选[M].北京：科学出版社，1991.16-19.

[5] 吴文俊.陈省身[A].中国大百科全书·数学卷[Z].北京：中国大百科全书出版社，1988.80.

[6] P.A.格列菲斯.对于陈省身数学贡献的一些感想[A].陈省身文选[M].北京：科学出版社，1991.

[7] 张洪光.陈省身——20世纪伟大的几何学家[A].科学巨星——世界著名科学家评传(1)[M].西安：陕西人民教育出版社，1995.1-71.

[8] 张洪光.陈省身[A].南开人物志·第一辑[M].天津：南开大学出版社，1999.213-223.

[9] 吴文俊.序：中央研究院数学研究所一年的回忆[A].陈省身文选[M].北京：科学出版社，1991.V-X.

[10] 陈省身.联大六年(1937—1943)[A].陈省身文选[M].北京：科学出版社，1991.12-13.

[11] 胡作玄.吴文俊[A].中国现代科学家传记·第二集[M].北京：科学出版社，1997.94-95.

[12] 周炜良.陈省身：朋友和数学家——写于他八十岁生日之际[J].潘建中译.数学译林，1998，(2)：127.

本文经授权转载自微信公众号“好玩的数学”，责任编辑：艾素珍。
原文发表于《中国科技史料》2000年第21卷第2期。

---

读《陈省身传》：数学，最能守持古典精神的科学

数学中国 2024 年 12 月 05 日 19 : 20 内蒙古

经典的数学优美，现代的数学除了优美，更有壮美。然而数学的精神，自从发皇于古希腊，古今一贯，从未中绝，一切的现代学问中，最能守持古典精神的，仍是数学。

一、“数学好玩”

陈省身先生去世八年了，但是读《陈省身传》，使我觉得这位大数学家仍然活着，声音笑貌，宛然目前。书中引了一首杨振宁的旧体诗，几千年的几何学历史，最简练的概括，就在诗句里：“千古寸心事，欧高黎嘉陈。”

《陈省身传》（修订版），张奠宙、王善平著，南开大学出版社 2011 年 10 月

几何学真的只是“寸心事”，几何学的历史真的只是“寸心”的传承与光大，而这“寸心”能运用于万汇物理，天衣有缝，依其剪接，微子聚力，赖其笼络，又真的是“浑然归一体，广邃妙绝伦”。陈省身自谦“罗汉”，但在几何学的殿堂里，他实在是一尊端坐于欧几里得、高斯、黎曼和嘉当之列的菩萨。《陈省身传》初版于传主的生前，这次修订再版，若干的增补中有一则趣事：陈省身临终前不久曾为少年数学爱好者题词：“数学好玩”；佛菩萨真的是触处见机，咳唾都是“心法”啊。

《陈省身传》的两位作者，主笔的是张奠宙教授。张教授是在泛函分析研究上取得过骄人成绩的数学专家，又是一位胸有全局的数学通人。“文革”结束不久，在国门依旧封闭的情况下，他就开始全面考察世界现代数学的发展和成就，历史轨迹和数学思想并重，所成《二十世纪数学史话》，启迪人至深，当时陈省身就非常称赞并着力推介。2002 年，张教授又成《二十世纪数学经纬》一书，内容加深加广，构思阔大，论述精到，较之“史话”，俨然一部有规模的现代数学通史了。《陈省身传》的另一位作者王善平是张教授的学生，他说自己“只是收集整理材料；当然，学到了很多”。是的，这样的书，就是读一遍，就是随便翻翻，也能“学到很多”，更不必说“整理材料”，参与写作了；这样的经验是那些为了“对得起”经费的课题写作无法比拟的。

两位作者还编过一本《陈省身文集》，主要收集陈省身的研究性论文之外的文字，但例外地收了陈省身自称“我一生最得意的工作”——《闭黎曼流形高斯 - 博内公式的一个简单的内蕴证明》一文；是王善平从美国《数学纪事》(Annals of Mathematics) 1944 年卷中译过来的。2002 年 8 月，第 24 届国际数学家大会在北京召开，张奠宙校、王善平译的《数学无国界》一书同时出版，这本书讲述一百年间国际数学家大会以及主办大会的国际数学联盟的历史，作者是曾任联盟主席的奥利·来赫托。书名传达了数学的真精神。2011 年，为了纪念陈省身百年诞辰而出版的《陈省身与几何学的发展》一书，编辑工作主要也是由王善平担任。这些书可以互相“链接”，不同需求的读者自能各取所需，开卷得益。

二、“经典的”与“现代的”

陈省身是一位不世出的几何学家，他有伟大的贡献。记得“文革”中毛主席会见杨振宁，曾说：“你是对人类作了贡献的人，我不是。”如果他会见陈省身，也当如是说。

众所周知，几何学是研究空间的性质和结构的。凭人类生而俱来的肉身感官，人们也许觉得空间很简单，还不是四方上下平直均匀无限延伸，有什么结构，谈什么性质。但是，一经数学用符号和数量关系把空间改制为抽象的、思想上的对象或实体，就大有文章可做了。

高斯用微积分的观点和方法，处理嵌在平直空间里的曲面，所得结果使思维进入新的层面：有充分的理由把曲面本身看作“内蕴空间”。空间就是曲面，曲面就是空间。人类直观到的三维空间，无非是加上时间以后四维空间里的一个“曲面”，或者说“超曲面”。空间可以是不平直的，可以处处有“曲率”；平直空间不过是曲率为 0 的曲面。

爱因斯坦研究引力作用、建立广义相对论时，已经有黎曼的曲面上的微分几何在等着他，爱翁是经由他的好朋友格罗斯曼的介绍，认识黎曼几何的。“广相”的结论竟然是：引力作用不是什么物与物之间的互相“吸引”，而是空间的“曲”性有以致之。

曲率是曲面的局部性质，曲面还有整体结构。同为橡胶制品，足球和汽车轮胎的表面显然是整体结构不同的；轮胎倒是和面包圈结构相同。不难想见，曲面的整体结构可以非常复杂，复杂到无以复加。所以微分几何先是研究曲面的局部性质，而后才发展出整体微分几何。整体微分几何需要用拓扑的观点看曲面，把它定义为“流形”(manifold)。

整体微分几何的兴起和发展，是一个起死回生的过程。1943 年陈省身初到普林斯顿，外出赴会，火车上邂逅一位美国有名的数学家。倾谈间，那位数学家听陈省身说是研究微分几何的，随口应道：“Oh！它死了！”经典微分几何在曲面局部性质上取得了许多优美成果，但因观点、方法、工具限于分析（即微积分）的范围，发展已臻止境，是死了。但这是火凤凰之死，她会重生，她会在更高的拓扑观点的观照下，在拓扑、代数、分析诸多工具的锤炼下重生。陈省身就是现代微分几何一位最重要的催生者和奠基者。

数学有“经典的”与“现代的”之分。发思古幽情的现代人，往往喜欢“经典的”东西，不喜欢“现代的”东西，文章、艺术、建筑，无不是古胜于今。数学不同，数学显然是“现代的”胜于“经典的”，现代数学把经典数学吃进去了，消化掉了，几乎没有排出什么“糟粕”；经典的数学优美，现代的数学除了优美，更有壮美。然而数学的精神，自从发皇于古希腊，古今一贯，从未中绝，一切的现代学问中，最能守持古典精神的，仍是数学。菲尔茨奖没有奖金，只有奖章，但它是数学界的最高荣誉，奖章上刻着的是古希腊阿基米德的头像。

1943 年至 1946 年，不到三年间，陈省身在普林斯顿从事现代微分几何的奠基工作，使得关于流形整体结构的纤维丛理论基本成形。他把高斯 - 博内公式从二维推广到高维；他把欧拉 - 庞加莱示性数、施蒂菲尔 - 惠特尼示性类等刻画整体的概念和局部的曲率联系起来；他又把一般微分流形的球丛推广到复流形上的复球丛，引进了一种全新的示性类，后来称为“陈类”(Chern Class)，时至今日，陈类已经是现代数学中的一个基本概念。

1945 年夏，陈省身在美国数学会大会上作题为“大范围微分几何若干新观点”的报告，系统阐述了整体微分几何的新思想和新方法。老一辈的拓扑学和几何学权威霍普夫听后评论说：“这篇演讲表明大范围微分几何的新时代开始了。这个新时代以纤维丛的拓扑理论和嘉当外微分方法的综合为特征。”半个世纪后，美国数学家辛格表达了所有追随和接续陈省身工作的学生后辈的共识：“陈省身就是现代微分几何。”菲尔茨奖得主邱成桐更明白宣示：“现代微分几何，嘉当是祖，陈省身是父。”

嘉当是陈省身的老师，他的外微分方法是一根“魔杖”，真懂和能用的人很少，连堪称希尔伯特之后最大数学家的外尔都说：“嘉当的书难读。”但陈省身掌握了这根魔杖，独得之秘，运用自如。1991 年张奠宙问过陈省身：“现在大家都能够很好地理解嘉当的思想了吗？”陈省身回答：“不一定。我可以保留这种秘密武器，别人做不出的结果，我可以做出来。”

1984 年，陈省身获沃尔夫奖，这个奖可以与菲尔茨奖并列，是数学的终身成就奖，颁奖词特别指出：“他在整体微分几何上的卓越贡献，其影响遍及整个数学。”被认为 20 世纪两项最伟大的数学成就之一的阿蒂亚 - 辛格指标定理（另一个是费尔马大定理的证明），也是以陈省身的工作为基础的。辛格在贺陈省身八十寿辰的文章中说：“对陈省身在局部和整体几何中能如此有效地运用微分形式感到惊异。”这所谓“微分形式”，就是陈省身的独得之秘，嘉当的魔杖。陈省身的同行们推崇他对现代几何的贡献，同时也欣羡他“对丰富和美丽的经典几何十分娴熟，这在数学界已经非常罕见”。

陈省身（1911 - 2004）是一位不世出的几何学家 （何籽 / 图）

三、几何与物理

陈省身一生的外在形迹，可以说很平常，很顺利，没有曲折的遭遇，没有离奇的故事；他的不平常，是他念兹在兹的精神世界，是他为数学建立的不朽功业。《陈省身传》的最大好处，就在于通过陈省身一生行事的叙述，忠实地、几乎又可以说是酣畅淋漓地再现了他的精神生活；同时，围绕着陈省身的数学成就，带出了一部现代几何学的历史及其诸多关联，特别是与物理学的关联。

书中涉及几何和物理的具体内容，某些概念、命题和论述不容易懂，但是张奠宙教授以其对所述内容的深刻理解和准确把握，出之以他所特有的通俗化本事，铺陈为文章，即使外行的读者，在似懂非懂之间，也能感受到现代高深数学和物理学的优美和壮美。

精彩的一例，杨振宁于 1954 年提出粒子物理学的规范场理论，流形上的纤维丛理论则是数学家在与物理完全无涉的情况下发展的，两者竟有高度的一致性，连各自的术语都能规整地一一对应。杨振宁弄清楚规范场与纤维丛的关系后，连呼“奇迹”，特地驱车前往陈省身的家中，两位科学大师共享奇迹的发现，赞叹之余，转生困惑，旧学新知，疑义相析，这正是穷究天人之际的学问商量啊。

讲完整个故事，作者有一段议论：“在发现规范场和纤维丛关系之前，陈省身很少关注物理。他只是埋头研究他钟爱的数学，把微分几何的房间打扫得清静干净，里面的物件井井有条，四周不乏华丽的装饰，使这所数学宫殿富丽堂皇。但是，当他打开窗户一看，外面是辽阔的物理学大海，清风徐来，海天一色，无限壮观，几何宫殿和物理大海竟然如此的和谐统一，只能感叹造化之巧。”这样的文字，能启发读者深思，引起同样的感叹。规范场和纤维丛，是用不同语言写的两篇大作，作者各不相谋，文章铢两悉称，仿佛互相的对译。这背后一定有更深的原因，原因何在呢？不在人际，在天人之际，在“道可道，非常道”的“造化之巧”。

陈、杨两家有特殊因缘，陈省身的丈人郑桐荪和杨振宁的父亲杨武之是清华同事，陈省身是他们的学生，后来也是同事；陈省身的婚事还是杨武之极力撮合的呢。杨振宁曾比喻数学与物理“像两片有共同根茎的树叶，顺着各自的脉络，奔赴生命的前程”。陈数学，杨物理，“各自奔赴生命的前程”，竟又在造极之境上欢然相会。“谁为为之？孰令听之？”造化的安排真是不可思议。

陈省身是握了道枢的人；这之后，他就经常讲几何与物理的关系了。1999 年，他在复旦大学演讲，主题是“物理就是几何”，一句话把牛顿、麦克斯韦、爱因斯坦、杨振宁一网打尽。你看牛顿的主要方程（第二定律），再看爱因斯坦的“广相”方程，写出来简单，都是一边几何量，一边物理量，“物理就是几何”。麦克斯韦电磁场方程很复杂，写出来一大堆，得占一整页，学者苦于难记；陈省身却能把它们简约为两个不能再短的式子：dA = F，δF = J，其解释是“纤维丛上有一个平行性，这个平行性的微分等于场的强度；而场的强度经过某个运算就得到它的流矢量”；仍是“物理就是几何”管着。最妙的是，杨振宁的规范场方程竟然也是这两个短式，当然解释不同。什么叫“茅塞顿开”？什么叫“豁然贯通”？什么叫“醍醐灌顶”？什么叫“一句顶一万句”？陈省身的话就是。陈省身已然顿悟，金针度人，向众生说法，任何人想要开悟，当然还得勤精渐修。陈省身已经把要做的功课开示了，有志者就依次修习吧。

四、“知其不知”与“知所不知”

陈省身说自己：“我会做数学，我也只会做数学。”但其实，他很有办事、行政的能力，他甚至“玩”过政治。晚年谈起西南联大事，他笑说：“我也会玩 politics，那年改选教授评议会，年轻的把年长的挤出去了，我是一个发动者。”这件事影响不小，还劳动校长梅贻琦的大驾，来找他“谈判”。陈省身认为管理国家，主要是政策好，方向对，管是不难的。新加坡总理李显龙在剑桥读过数学，陈省身借事发挥：“数学家可以管国家，而管国家的却做不了数学。”他好像有点瞧不起政治。

他领导过好几个研究所，宗旨始终是：“凡有利于数学的，总要去做；凡与数学无关的，请勿打扰。”他说：“我办事的原则就是少管事。办研究所最要紧的是把有能力的数学家和学生找来聚在一起，之后就不要管了。”他对申请经费之类有点头痛：“动不动就要你的计划，但是照计划做出来的不会是最有价值的，最好没有计划。”好在陈省身是尊菩萨，管钱的愿意借花献佛，大有人在。陈省身研究、教学、办事、行政，都是为了数学的利益，他个人的荣誉和利益，是与数学的利益完全一致的。

陈省身经常说：“数学没有诺贝尔奖是幸事。”数学没有诺奖，但有菲尔茨奖、沃尔夫奖、阿贝尔奖、罗巴切夫斯基奖、维布伦奖等等。有什么区别吗？重要的区别在于：诺奖已经严重地大众化了，诺奖已经是大众社会（mass society）里的事了，诺奖得主与大众的关系已经是“明星”与“粉丝”的关系了。

你到街上取样，随机抓十个人来问，人人知道诺奖，几乎没人知道菲奖或沃奖，遑论维奖、罗奖、阿贝尔奖。2002 年北京开国际数学家大会，中国的媒体上最出风头的不是那一年的菲奖得主，也不是那届大会上做一小时报告的人；最出风头的两位，一位是坐在轮椅里研究宇宙学的物理学家霍金，另一位是得了经济学诺奖的数学家纳什。纳什肯定不懂经济学，却由于一篇他自己都认为“不起眼”的数学论文引发许多经济学研究，而得了经济学诺奖；他数学了得，心心念念想得菲奖，总不遂愿，因此精神一度失常，也属失计。菲奖是懂行同行的肯定和评价，是自然之光下的最高荣誉；诺奖也是，但在诺奖，自然之光被舞台之光掩蔽，舞台之下是 mass。mass 另有木知木觉块然大物一义，蠢动起来，势如飓风，力能崩山，明星与 mass，真不知道谁播弄谁。没有诺奖，对于数学“这片安静的世界”确实是幸事。

南朝释慧皎撰《高僧传》，自序里说：“前代所撰，多曰名僧。然名者，本实之宾也。若实行潜光，则高而不名；寡德适时，则名而不高。”于是区分了“高”和“名”。其实“高”也是“名”，“高”是高名，“名”是大名。诺奖与菲奖、沃奖的区别在于：诺之高名，可能被大名所掩，菲、沃则否。陈省身、邱成桐师徒，都是既高且名的大师；当今数学家，高而不名者，有一人焉，俄罗斯人佩雷尔曼。佩氏在本世纪初成功证明了庞加莱猜想，这是克莱研究所公布的新千禧年七大数学难题的第一题。2006 年国际数学联盟给他菲尔茨奖，他没有要；2011 年克莱研究所给他百万美元奖金，他也没有要。他说：“如果我的证明是正确的，就不需要任何其他形式的肯定。”

佩雷尔曼也许是截断众流的孤傲，陈省身则精神内守，而又随波逐浪，佩氏大推开，陈氏大洒脱，二者皆好。依佛老语说，陈省身更为圆熟，佩雷尔曼毕竟不是中国人。但若言数学精神的直接呈现，则似乎佩氏更为昭彰。数学是一项值得人为了她的自身，而不是为了她所能带来的东西而从事的事业。数学的成就是自我界定的，不像跳高、跑快之类，必须从外面、用奖金名次等来界定，不求名次奖金，一天到夜练跑快，那是练傻。陈省身经常说：“为了个人名利，数学不是一条坦途。”名利之徒进入数学，他得有所改正。人说政治是屁股指挥脑袋，我说数学能脑袋端正屁股。

苏格拉底认定最高最幸福的生活是哲人的生活，是追求知识。《陈省身传》的作者则称“数学家的精神毋宁说是诗人的或哲学家的。他们是发现和讴歌自然秩序的美的诗人，是寻找精神归宿和营造精神家园的哲人”。数学精神的源头在古希腊哲人那里。

“追求知识”的题中应有之义是知识不能被占有，所以没有“智者”(sophist)；如果知识比作财富，“智者”就是大富翁，然而知识不是财富。哲人的基本状态是“不知”，追求知识的前提是“知其不知”，所以真正的知识必然是“无知之知”(knowledge about ignorance)。

怎样才能建立追求知识的前提，“知其不知”呢？善解古希腊哲人精义的现代大哲列奥·施特劳斯像庄子一样说话了：“不知其不知，以不知其所不知也。”(One can not know that one does not know without knowing what one does not know。)陈省身以九十岁的高龄，还在研究“六维球面上是否存在复结构”的难题，他深知“所不知”在哪里，故知其不知，而不安于不知，在“所不知”的指引下努力探索，精神明显是古希腊的。陈省身平时说话，喜欢借佛语、庄子语，但临终却说：“我要去希腊朝圣了。”

庄子也教人“知其不知”，但主张安于不知，“弃圣绝智”。这境界也好，“不求甚解，每有会意，欣然忘食”的五柳先生便是这境界里的一个典型。但如果五柳先生忘食而未尝忘言，舌粲莲花，滔滔不绝之下，恐怕会陷于“不知其不知”，而自以为知了。五柳先生，可是“现代的”大不如“经典的”啊。

来源：南方周末

---

via:

• From Triangles to Manifolds - TrianglesToMfds.pdf…
  https://paperzz.com/doc/7117637/from-triangles-to-manifolds-shing

• 陈省身：数学陶冶我一生
  https://mp.weixin.qq.com/s/iyZispLbapBw3TWDr5ZvOA

• 陈省身访谈录：数学是我唯一能做的事
  https://mp.weixin.qq.com/s/PiCMawrjsLQqg5bKzFV4rw

• 陈省身访谈录：科学上最伟大的发现都不是有计划的
  https://mp.weixin.qq.com/s/S3CIEa-8JlcPVlcIfrCiSA

• 读《陈省身传》：数学，最能守持古典精神的科学
  https://mp.weixin.qq.com/s/-bgioE7-1yUQX9B9v7Xftw