Apollo代码学习(六)—模型预测控制(MPC)

前言

非专业选手，此篇博文内容基于书本和网络资源整理，可能理解的较为狭隘，起点较低，就事论事。如发现有纰漏，请指正，非常感谢！！！

查看Apollo中关于MPC_controller的代码可以发现，它的主体集成了横纵向控制，在计算控制命令时，计算了横纵向误差：

ComputeLongitudinalErrors(&trajectory_analyzer_, debug);

ComputeLateralErrors(com.x(), com.y(),
                       VehicleStateProvider::instance()->heading(),
                       VehicleStateProvider::instance()->linear_velocity(),
                       VehicleStateProvider::instance()->angular_velocity(),
                       trajectory_analyzer_, debug);

下文将从MPC原理入手，结合横纵向控制进行分析。

模型预测控制

可以先结合官方的教学视频对MPC进行一个简单的了解：模型预测控制。

根据维基百科，模型预测控制是一种先进的过程控制方法，在满足一定约束条件的前提下，被用来实现过程控制，它的实现依赖于过程的动态模型（通常为线性模型）。在控制时域（一段有限时间）内，它主要针对当前时刻进行优化，但也考虑未来时刻，求取当前时刻的最优控制解，然后反复优化，从而实现整个时域的优化求解。

也就是说，模型预测控制实际上是一种时间相关的，利用系统当前状态和当前的控制量，来实现对系统未来状态的控制。而系统未来的状态是不定的，因此在控制过程中要不断根据系统状态对未来的控制量作出调整。而且相较于经典的的PID控制，它具有优化和预测的能力，也就是说，模型预测控制是一种致力于将更长时间跨度、甚至于无穷时间的最优化控制问题，分解为若干个更短时间跨度，或者有限时间跨度的最优化控制问题，并且在一定程度上仍然追求最优解¹。

可以通过下图对模型预测控制进行一个简单的理解：

图1 模型预测控制原理 (图片来源：无人驾驶车辆模型预测控制)

图1中，k轴为当前状态，左侧为过去状态，右侧为将来状态。可结合无人驾驶车辆模型预测控制²第3.1.2节来理解此图。

模型预测控制在实现上有三个要素：

1. 预测模型，是模型预测控制的基础，用来预测系统未来的输出；
2. 滚动优化，一种在线优化，用于优化短时间内的控制输入，以尽可能减小预测模型输出与参考值的差距；
3. 反馈矫正，在新的采样时刻，基于被控对象的实际输出，对预测模型的输出进行矫正，然后进行新的优化，以防模型失配或外界干扰导致的控制输出与期望差距过大。

下面从三要素入手对模型预测控制进行分析。

预测模型

无论是运动学模型，还是动力学模型，所搭建的均为非线性系统，而线性模型预测控制较非线性模型预测控制有更好的实时性，且更易于分析和计算。对于无人车来说，实时性显然很重要，因此，需要将非线性系统转化为线性系统，而非线性系统的线性化的方法大体可分为精确线性化和近似线性化，多采用近似的线性化方法。

线性化

此部分内容主要参考《无人驾驶车辆模型预测控制》²3.3.2节，本人对对线性化、离散化等问题也理解的不深，不理解的可以自行查找一些其他的文章。

非线性系统线性化的方法有很多种，大致分为：

图2 线性化方法

下面以泰勒展开的方法为例，结合《无人驾驶车辆模型预测控制》²3.3.2节非线性系统线性化方法，展示一种存在参考系统的线性化方法。存在参考系统的线性化方法假设参考系统已经在规划轨迹上完全跑通，得出每个时刻上相应的状态量$X_r$和控制量$U_r$，然后通过处理参考系统与当前系统的偏差，利用模型预测控制器来跟踪期望路径。

假设车辆参考系统在任意时刻的状态和控制量满足如下方程：
$${\dot{X}}_r=f(X_r,U_r)\text{\hspace{1em}(1)}$$
在任意点$(X_r,U_r)$处泰勒展开，只保留一阶项，忽略高阶项，有：
$$\dot{X}=f(X_r,U_r)+\frac{\partial f}{\partial X}(X-X_r)+\frac{\partial f}{\partial U}(U-U_r)\text{\hspace{1em}(2)}$$
公式2与公式1相减可得：
$$\dot{\tilde{X}}=A(t)\tilde{X}+B(t)\tilde{U}\text{\hspace{1em}(3)}$$
其中，$\dot{\tilde{X}}=\dot{X}-{\dot{X}}_r$，$\tilde{X}=X-X_r$，$\tilde{U}=U-U_r$，$A(t)$为$f(X,U)$对$X$的雅克比矩阵，$B(t)$为$f(X,U)$对$U$的雅克比矩阵。
此时，通过雅克比矩阵，将非线性系统近似转化为一个连续的线性系统，但并不适于模型预测控制器的设计，然后对其离散化处理可得，
$$\dot{\tilde{X}}(k)=\frac{\tilde{X}(k+1)-\tilde{X}(k)}{T}=A(k)\tilde{X}(k)+B(k)\tilde{U}(k)\text{\hspace{1em}(4)}$$
得到线性化时变模型：
$$\tilde{X}(k+1)=\tilde{A}(k)\tilde{X}(k)+\tilde{B}(k)\tilde{U}(k)\text{\hspace{1em}(5)}$$
其中：$\tilde{A}(t)=I+TA(t)，\tilde{B}(t)=TB(t)，I$为单位矩阵。

至此，得到一个非线性系统在任意一参考点线性化后的线性系统，该系统是设计模型预测控制算法的基础。

以运动学模型中的式1.15为例，低速情况下的车辆运动学模型可表达为：
$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{c}\cos \psi \\ \sin \psi \\ \tan {\delta }_f/l\end{array}\right]v\text{\hspace{1em}(6)}$$
其状态变量和控制变量分别为：
$$X=\left[\begin{array}{c}x\\ y\\ \psi \end{array}\right]，U=\left[\begin{array}{c}v\\ {\delta }_f\end{array}\right]$$
对应的雅克比矩阵：
$$A=\left[\begin{array}{ccc}0& 0& -v\sin \psi \\ 0& 0& v\cos \psi \\ 0& 0& 0\end{array}\right]，B=\left[\begin{array}{cc}\cos \psi & 0\\ \sin \psi & 0\\ \frac{\tan {\delta }_f}{l}& \frac{v}{l{\cos }^2{\delta }_f}\end{array}\right]\text{\hspace{1em}(7)}$$
其线性时变模型为：
$$\dot{\tilde{X}}=\tilde{A}\tilde{X}+\tilde{B}\tilde{U}$$
其中，
$$\begin{gathered} \tilde{X}=\left[\begin{array}{c}x-x_0\\ y-y_0\\ \psi -{\psi }_0\end{array}\right]，\tilde{U}=\left[\begin{array}{c}v-v_0\\ {\delta }_f-{\delta }_{f0}\end{array}\right]， \\ \tilde{A}=I+TA=\left[\begin{array}{ccc}1& 0& -v\sin \psi T\\ 0& 1& v\cos \psi T\\ 0& 0& 1\end{array}\right]，\tilde{B}=TB=\left[\begin{array}{cc}\cos \psi T& 0\\ \sin \psi T& 0\\ \frac{\tan {\delta }_{f}T}{l}& \frac{vT}{l{\cos }^2{\delta }_f}\end{array}\right]\text{\hspace{1em}(8)} \end{gathered}$$

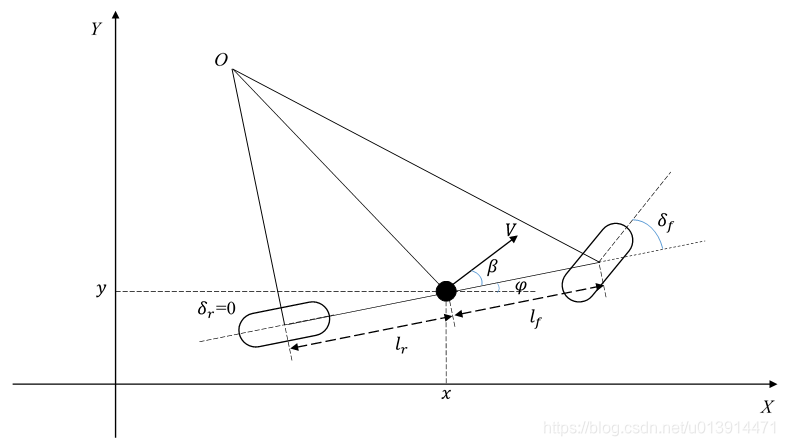
单车模型

预测模型仍以单车模型为主，结合运动学模型和动力学模型对车辆运动状态进行分析。

图3 单车模型

根据化代码可知，Apollo的MPC模块中的状态变量共有6个：

  matrix_state_ = Matrix::Zero(basic_state_size_, 1);
  
  // State matrix update;
  matrix_state_(0, 0) = debug->lateral_error();
  matrix_state_(1, 0) = debug->lateral_error_rate();
  matrix_state_(2, 0) = debug->heading_error();
  matrix_state_(3, 0) = debug->heading_error_rate();
  matrix_state_(4, 0) = debug->station_error();
  matrix_state_(5, 0) = debug->speed_error();

$$matrix\_state\_=\left[\begin{array}{c}lateral\_error\\ lateral\_error\_rate\\ heading\_error\\ heading\_error\_rate\\ station\_error\\ speed\_error\end{array}\right]$$
它们的计算请参考上一篇Apollo代码学习(五)—横纵向控制：
$$\{\begin{array}{l}matrix\_state\_(0,0)=dy\ast \cos \phi -dx\ast \sin \phi \\ matrix\_state\_(1,0)=V_x\ast \sin \Delta \phi =V_x\ast \sin e_2\\ matrix\_state\_(2,0)=\phi -{\phi }_{des}\\ matrix\_state\_(3,0)=\dot{\phi }-{\dot{\phi }}_{des}\\ matrix\_state\_(4,0)=-(dx\ast \cos {\phi }_{des}+dy\ast \sin {\phi }_{des})\\ matrix\_state\_(5,0)=V_{des}-V\ast \cos \Delta \phi /k\end{array}$$
控制变量有2个：

  Eigen::MatrixXd control_matrix(controls_, 1);
  control_matrix << 0, 0;

并结合代码去分析$control\_matrix$内包含的变量：

// 解mpc，输出一个vector，control内有10个control_matrix
SolveLinearMPC(matrix_ad_, matrix_bd_, matrix_cd_, matrix_q_updated_,
          matrix_r_updated_, lower_bound, upper_bound, matrix_state_, reference,
          mpc_eps_, mpc_max_iteration_, &control)
// 已知，mpc仅取第一组解为当前时刻最优控制解，即control[0]
// control中第一个矩阵中的第一个值用于计算方向盘转角
double steer_angle_feedback = control[0](0, 0) * 180 / M_PI *
                                steer_transmission_ratio_ /
                                steer_single_direction_max_degree_ * 100;
double steer_angle = steer_angle_feedback + steer_angle_feedforwardterm_updated_;
// control中第一个矩阵中的第二个值用于计算加速度
debug->set_acceleration_cmd_closeloop(control[0](1, 0));
double acceleration_cmd = control[0](1, 0) + debug->acceleration_reference();

可得
$$control\_matrix=\left[\begin{array}{c}{\delta }_f\\ a\end{array}\right]$$
其中，${\delta }_f$为前轮转角，$a$为加速度补偿。
结合方向盘控制的动力学模型：
$$\begin{gathered} \frac{d}{dt}\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{2C_{af}+2C_{ar}}{m{V}_x}& \frac{2C_{af}+2C_{ar}}{m}& \frac{-2C_{af}{\ell }_f+2C_{ar}{\ell }_r}{m{V}_x}\\ 0& 0& 0& 1\\ 0& -\frac{2C_{af}{\ell }_f-2C_{ar}{\ell }_r}{I_z{V}_x}& \frac{2C_{af}{\ell }_f-2C_{ar}{\ell }_r}{I_z}& -\frac{2C_{af}{\ell }_f^2+2C_{ar}{\ell }_r^2}{I_z{V}_x}\end{array}\right]\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right] \\ +\left[\begin{array}{c}0\\ \frac{2C_{\alpha f}}{m}\\ 0\\ \frac{2C_{\alpha f}{\ell }_f}{I_z}\end{array}\right]{\delta }_f+\left[\begin{array}{c}0\\ -\frac{2C_{af}{\ell }_f-2C_{ar}{\ell }_r}{m{V}_x}-V_x\\ 0\\ -\frac{2C_{af}{\ell }_f^2+2C_{ar}{\ell }_r^2}{I_z{V}_x}\end{array}\right]\dot{\phi }\text{\hspace{1em}(9)} \end{gathered}$$
和mpc_controller.cc、mpc_slover.cc中的代码注释，

// 初始化矩阵
Status MPCController::Init(const ControlConf *control_conf) {
  ...
  // Matrix init operations.
  matrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_);
  matrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_);
  ...
  // TODO(QiL): expand the model to accomendate more combined states.

  matrix_a_coeff_ = Matrix::Zero(basic_state_size_, basic_state_size_);
  ...

  matrix_b_ = Matrix::Zero(basic_state_size_, controls_);
  matrix_bd_ = Matrix::Zero(basic_state_size_, controls_);
  ...
  matrix_bd_ = matrix_b_ * ts_;

  matrix_c_ = Matrix::Zero(basic_state_size_, 1);
  ...
  matrix_cd_ = Matrix::Zero(basic_state_size_, 1);
  ...
  }

// 更新矩阵
void MPCController::UpdateMatrix(SimpleMPCDebug *debug) {
  const double v = VehicleStateProvider::instance()->linear_velocity();
  matrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;
  matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;
  matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;
  matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;

  Matrix matrix_i = Matrix::Identity(matrix_a_.cols(), matrix_a_.cols());
  matrix_ad_ = (matrix_i + ts_ * 0.5 * matrix_a_) *
               (matrix_i - ts_ * 0.5 * matrix_a_).inverse();

  matrix_c_(1, 0) = (lr_ * cr_ - lf_ * cf_) / mass_ / v - v;
  matrix_c_(3, 0) = -(lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_ / v;
  matrix_cd_ = matrix_c_ * debug->heading_error_rate() * ts_;
}

// 求解MPC
// discrete linear predictive control solver, with control format
// x(i + 1) = A * x(i) + B * u (i) + C
bool SolveLinearMPC(const Matrix &matrix_a, const Matrix &matrix_b,
                    const Matrix &matrix_c, const Matrix &matrix_q,
                    const Matrix &matrix_r, const Matrix &matrix_lower,
                    const Matrix &matrix_upper,
                    const Matrix &matrix_initial_state,
                    const std::vector<Matrix> &reference, const double eps,
                    const int max_iter, std::vector<Matrix> *control) 

可得MPC控制模型：
$$\begin{gathered} \frac{d}{dt}\left[\begin{array}{c}lateral\_error\\ lateral\_error\_rate\\ heading\_error\\ heading\_error\_rate\\ station\_error\\ speed\_error\end{array}\right]=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 0& -\frac{C_f+C_r}{mV}& \frac{C_f+C_r}{m}& \frac{C_r{\ell }_r-C_f{\ell }_f}{mV}& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& \frac{C_r{\ell }_r-C_f{\ell }_f}{I_{z}V}& \frac{C_f{\ell }_f-C_r{\ell }_r}{I_z}& -\frac{C_r{\ell }_r^2+C_f{\ell }_f^2}{I_{z}V}& 0& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}lateral\_error\\ lateral\_error\_rate\\ heading\_error\\ heading\_erro{r}_{r}ate\\ station\_error\\ speed\_error\end{array}\right] \\ +\left[\begin{array}{cc}0& 0\\ \frac{C_f}{m}& 0\\ 0& 0\\ \frac{C_f{\ell }_f}{I_z}& 0\\ 0& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}{\delta }_f\\ a\end{array}\right]+\left[\begin{array}{c}0\\ \frac{C_r{\ell }_r-C_f{\ell }_f}{mV}-V\\ 0\\ -\frac{C_r{\ell }_r^2+C_f{\ell }_f^2}{I_{z}V}\\ 0\\ 1\end{array}\right]\dot{\phi }\text{\hspace{1em}(10)} \end{gathered}$$

其中，$C_f，C_r$分别为前/后轮转弯刚度，${\ell }_f，{\ell }_r$分别为前悬/后悬长度，$m$为车身质量，$V$为车速，$I_z$为车辆绕$z$轴转动的转动惯量，$\dot{\phi }$为转向速度。
对应的状态矩阵、控制矩阵、扰动矩阵等如下：
$$\begin{gathered} A=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 0& -\frac{C_f+C_r}{mV}& \frac{C_f+C_r}{m}& \frac{C_r{\ell }_r-C_f{\ell }_f}{mV}& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& \frac{C_r{\ell }_r-C_f{\ell }_f}{I_{z}V}& \frac{C_f{\ell }_f-C_r{\ell }_r}{I_z}& -\frac{C_r{\ell }_r^2+C_f{\ell }_f^2}{I_{z}V}& 0& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0\end{array}\right]， \\ B=\left[\begin{array}{cc}0& 0\\ \frac{C_f}{m}& 0\\ 0& 0\\ \frac{C_f{\ell }_f}{I_z}& 0\\ 0& 0\\ 0& -1\end{array}\right]，C=\left[\begin{array}{c}0\\ \frac{C_r{\ell }_r-C_f{\ell }_f}{mV}-V\\ 0\\ -\frac{C_r{\ell }_r^2+C_f{\ell }_f^2}{I_{z}V}\\ 0\\ 1\end{array}\right]\text{\hspace{1em}(11)} \end{gathered}$$
对应的线性化系数应为（欧拉映射离散法）：
$$\tilde{A}=I+TA，\tilde{B}=TB，\tilde{C}=TC$$
但代码中实际线性化系数为（双线性变换离散法）：

  matrix_ad_ = (matrix_i + ts_ * 0.5 * matrix_a_) *
               (matrix_i - ts_ * 0.5 * matrix_a_).inverse();
               
  matrix_bd_ = matrix_b_ * ts_;

  matrix_cd_ = matrix_c_ * debug->heading_error_rate() * ts_;

$$\tilde{A}=(I+TA/2)(I-TA/2{)}^{-1}，\tilde{B}=TB，\tilde{C}=TC\ast heading\_error\_rate\text{\hspace{1em}(12)}$$
对于$\tilde{C}$的形式不同，个人认为是由于$heading\_error\_rate$是计算横向误差之后才有的，无法直接获取，在矩阵更新的时候才将$heading\_error\_rate$作为系数更新到矩阵中，也就是公式10中的$\dot{\phi }$，其实对于$\tilde{C}$来说，仍是$\tilde{C}=TC$的形式。$\tilde{A}$的形式不一样，是因为此处采用了双线性变换离散法。感谢博友LLCCCJJ的友情提示。 关于连续系统离散化的方法可参考：连续系统离散化方法。

最终得到形如公式13的离散线性模型：
$$x(k+1)=Ax(k)+Bu(k)+C\text{\hspace{1em}(13)}$$
系统的输出方程为：$y(k)=Dx(k)$。
则在预测时域内有状态变量方程和输出变量方程如下：
$$x(k)=A^{k}x(0)+\sum _{i=0}^{k-1}{A}^{i}Bu(k-1-i)+\sum _{i=0}^{k-1}{A}^{i}C\text{\hspace{1em}(14)}$$
$$y(k)=D{A}^{k}x(0)+\sum _{i=0}^{k-1}D{A}^{i}Bu(k-1-i)+\sum _{i=0}^{k-1}D{A}^{i}C\text{\hspace{1em}(15)}$$
假设
$$\xi (k|t)=\left[\begin{array}{c}x(k|t)\\ u(k-1|t)\end{array}\right]\text{\hspace{1em}(16)}$$
可得到新的状态空间表达式：
$$\begin{array}{c}\xi (k+1|t)=\tilde{A}\xi (k|t)+\tilde{B}\Delta u(k|t)+\tilde{C}\\ \eta (k|t)=\tilde{D}\xi (k|t)\end{array}\text{\hspace{1em}(17)}$$
其中，
$$\begin{array}{c}\tilde{A}=\left[\begin{array}{cc}A& B\\ 0& I\end{array}\right]，\tilde{B}=\left[\begin{array}{c}B\\ I\end{array}\right],\tilde{C}=\left[\begin{array}{c}C\\ 0\end{array}\right],\tilde{D}=[D0]\end{array}\text{\hspace{1em}(18)}$$
可将公式16、公式18代入公式17，验证公式18的由来。
则在预测时域内的状态变量和输出变量可用如下算式计算：
$$\begin{array}{c}\xi (k+N_p|t)={\tilde{A}}_t^{N_p}\xi (t|t)+{\tilde{A}}_t^{N_p-1}{\tilde{B}}_t\Delta u(t|t)+{\tilde{A}}_t^{N_p-1}{\tilde{C}}_t+\cdots +{\tilde{B}}_t\Delta u(t+N_p-1|t)+{\tilde{C}}_t\\ \eta (k+N_p|t)={\tilde{D}}_t{\tilde{A}}_t^{N_p}\xi (t|t)+{\tilde{D}}_t{\tilde{A}}_t^{N_p-1}{\tilde{B}}_t\Delta u(t|t)+{\tilde{D}}_t{\tilde{A}}_t^{N_p-1}{\tilde{C}}_t+\cdots +{\tilde{D}}_t{\tilde{B}}_t\Delta u(t+N_p-1|t)+{\tilde{D}}_t{\tilde{C}}_t\end{array}\text{\hspace{1em}(19)}$$
将系统未来时刻的状态和输出以矩阵形式表达为：
$$\begin{array}{c}X(t)={\Psi }_t\xi (t|t)+{\Phi }_t\Delta U(t|t)+{{\rm Y}}_t\\ Y(t)={\tilde{D}}_{t}X(t)\end{array}\text{\hspace{1em}(20)}$$
其中，
$$\begin{gathered} X(t)=\left[\begin{array}{c}\xi (t+1|t)\\ \xi (t+2|t)\\ \xi (t+3|t)\\ ⋮\\ \xi (t+N_p|t)\end{array}\right],Y(t)=\left[\begin{array}{c}\eta (t+1|t)\\ \eta (t+2|t)\\ \eta (t+3|t)\\ ⋮\\ \eta (t+N_p|t)\end{array}\right],\Delta U=\left[\begin{array}{c}\Delta u(t|t)\\ \Delta u(t+1|t)\\ \Delta u(t+2|t)\\ ⋮\\ \Delta u(t+N_p-1|t)\end{array}\right],{{\rm Y}}_t=\left[\begin{array}{c}\tilde{C}\\ \tilde{A}\tilde{C}+\tilde{C}\\ {\tilde{A}}^2\tilde{C}+\tilde{A}\tilde{C}+\tilde{C}\\ ⋮\\ {\sum }_{i=0}^{N_p-1}{\tilde{A}}^i\tilde{C}\end{array}\right], \\ {\Psi }_t=\left[\begin{array}{c}{\tilde{A}}_t\\ {\tilde{A}}_t^2\\ {\tilde{A}}_t^3\\ ⋮\\ {\tilde{A}}_t^{N_p}\end{array}\right],{\Phi }_t=\left[\begin{array}{ccccc}{\tilde{B}}_t& 0& 0& \cdots & 0\\ {\tilde{A}}_t{\tilde{B}}_t& {\tilde{B}}_t& 0& \cdots & 0\\ ⋮& ⋮& \cdots & \cdots & \cdots \\ {\tilde{A}}_t^{N_p-1}{\tilde{B}}_t& {\tilde{A}}_t^{N_p-2}{\tilde{B}}_t& \cdots & \cdots & {\tilde{B}}_t\end{array}\right]\text{\hspace{1em}(21)} \end{gathered}$$
通过公式20我们可以看出，预测时域内的状态和输出量都可以通过从系统当前的状态量$\xi (t|t)$和控制增量$\Delta U(t|t)$求得，这也即是模型预测控制算法中“预测”功能的实现。
结合mpc_slover.cc，对MPC的模型进行分析：

  unsigned int horizon = reference.size();  // horizon =10

  // Update augment reference matrix_t
  // matrix_t为60*1的矩阵，存储的参考轨迹信息
  Matrix matrix_t = Matrix::Zero(matrix_b.rows() * horizon, 1);
  ...

  // Update augment control matrix_v
  // matrix_v为20*1的矩阵，存储控制信息
  Matrix matrix_v = Matrix::Zero((*control)[0].rows() * horizon, 1);
  ...

  // matrix_a_power为含有10个矩阵的容器，每个矩阵为6*6，matrix_a为6*6矩阵
  std::vector<Matrix> matrix_a_power(horizon);
  ...

  // matrix_k为60*20的矩阵，matrix_b为6*2矩阵
  Matrix matrix_k =
      Matrix::Zero(matrix_b.rows() * horizon, matrix_b.cols() * horizon);
  ...  

令$Ref=matrix\_t,Ctr=matrix\_v,A=matrix\_a,AP=matrix\_a\_power,B=matrix\_b,K=matrix\_k$，根据代码有：
$$\begin{gathered} Ref=\left[\begin{array}{c}re{f}_1\\ re{f}_2\\ ⋮\\ re{f}_{10}\end{array}\right],Ctr=\left[\begin{array}{c}ct{r}_1\\ ct{r}_2\\ ⋮\\ ct{r}_{10}\end{array}\right],PA=\left[\begin{array}{c}A\\ A^2\\ ⋮\\ A^{10}\end{array}\right], \\ K=\left[\begin{array}{cccc}AB& 0& \cdots & 0\\ A^{2}B& AB& \cdots & 0\\ ⋮& ⋮& \cdots & ⋮\\ A^{10}B& A^{9}B& \cdots & AB\end{array}\right]\text{\hspace{1em}(22)} \end{gathered}$$
其中，$re{f}_i$为参考轨迹序列，$ct{r}_i$为预测控制序列，预测时域为10个采样周期。

滚动优化

MPC的线性优化问题可以结合无人驾驶车辆模型预测控制第3.3.1节及以下文章：Model predictive control of a mobile robot using linearization进行学习。

滚动优化的目的是为了求最优控制解，是一种在线优化，它每一时刻都会针对当前误差重新计算控制量，通过使某一或某些性能指标达到最优来实现控制作用。因此，滚动优化可能不会得到全局最优解，但是却能对每一时刻的状态进行最及时的响应，达到局部最优。

因此，需要设计合适的优化目标，以获得尽可能最优的控制序列，目标函数的一般形式可表示为状态和控制输入的二次函数：
$$J(k)=\sum _{j=1}^N(\tilde{x}(k+j|k{)}^{T}Q\tilde{x}(k+j|k)+\tilde{u}(k+j-1|k{)}^{T}R\tilde{u}(k+j-1|k))\text{\hspace{1em}(23)}$$

其中，$N$为预测时域，$Q,R$为权重矩阵，且满足$Q\ge 0,R>0$的正定矩阵。形如$a(m|n)$表示，在$n$时刻下预测的$m$时刻的$a$值。第一项反映了系统对参考轨迹的跟踪能力，第二项反映了对控制量变化的约束。此外，上式（公式23）在书写过程中，累加和函数$\sum$后几乎都不加"()"，但我看起来实在难受，所以自行将$x,u$一起括起来。
优化求解的问题可以理解为在每一个采样点$k$，寻找一组最优控制序列${\tilde{u}}_t^{\ast }$和最优开销$J^{\ast }(k)$，其中:
$${\tilde{u}}_t^{\ast }=\arg \underset{\tilde{u}}{\min }J(k)$$
在MPC控制规律中，将控制序列中的第一个参数作为控制量，输入给被控系统。

对于车辆控制来说，就是找到一组合适的控制量，如$u=[{\delta }_f,a{]}^T$，其中，${\delta }_f$为前轮偏角，$a$为刹车/油门系数，使车辆沿参考轨迹行驶，且误差最小、控制最平稳、舒适度最高等。因此在设计目标函数的时候可以考虑以下几点：

1. 看过Apollo官方控制模块视频的人，可能知道在设计代价函数时候，一般设计为二次型的样式，为的是避免在预测时域内，误差忽正忽负，导致误差相互抵消；此外，对于实在不理解为什么代价函数要采用平方形式的同学，也可以参考损失函数为什么用平方形式（二）。
2. 可考虑的代价有：
   a. 距离误差(Cross Track Error, CTE)，指实际轨迹点与参考轨迹点间的距离，误差项可表示为：$(z_i-z_{ref,i}{)}^2$；
   b. 速度误差，指实际速度与期望速度的差，误差项可表示为：$(v_i-v_{ref,i}{)}^2$；
   c. 刹车/油门调节量，目的是为了保证刹车/油门变化的平稳性，误差项可表示为：$(a_{i+1}-a_i{)}^2$；
   d. 航向误差等…
3. 约束条件
   a. 最大前轮转角
   b. 最大刹车/油门调节量
   c. 最大方向盘转角
   d. 最大车速等

因此公式23中的第一项可表示为：
$$\sum _{j=1}^N\tilde{x}(k+j|k{)}^{T}Q\tilde{x}(k+j|k)=\sum _{j=1}^N(w_1(z_i-z_{ref,i}{)}^2+w_2(v_i-v_{ref,i}{)}^2+w_3(a_{i+1}-a_i{)}^2+...)\text{\hspace{1em}(24)}$$
其中，$w_i$为该项误差的权重，对应权重矩阵Q中的某一项。

对于上述的目标函数（公式23），是有多个变量，且要服从于这些变量的线性约束的二次函数，因此可以通过适当处理将其转换为二次规划问题。

基于公式20，将控制量变为控制增量，以满足系统对控制增量的要求，则目标函数可以改写为：
$$J(\xi (t),u(t-1),\Delta U(t))=\sum _{i=1}^N||\eta (t+i|t)-{\eta }_{ref}(t+i|t)|{|}_Q^2+\sum _{i=1}^{N-1}||\Delta U(t+i|t)|{|}_R^2\text{\hspace{1em}(25)}$$

在此基础上满足一些约束条件，一般如下：

$$\{\begin{array}{l}控制量约束:u_{min}(t+k)\le u(t+k)\le u_{max}(t+k)\\ 控制增量约束:\Delta u_{min}(t+k)\le \Delta u(t+k)\le \Delta u_{max}(t+k)\\ 输出约束:y_{min}(t+k)\le y(t+k)\le y_{max}(t+k)\end{array}\text{\hspace{1em}(26)}$$
其中，$k=0,1,2,3,...,N-1$。

将公式20代入公式23中，并将预测时域内输出量偏差表示为：
$$E(t)={\Psi }_t\xi (t|t)-Y_{ref}(t)\text{\hspace{1em}(27)}$$
其中，$Y_{ref}=[{\eta }_{ref}(t+1|t),...,{\eta }_{ref}(t+N|t){]}^T$。
经过一定的矩阵计算，可将目标函数调整为与控制增量相关的函数：
$$J(\xi (t),u(t-1),\Delta U(t))=\Delta U(t)H_t\Delta U(t{)}^T+G_t\Delta U(t{)}^T+P_t\text{\hspace{1em}(28)}$$
其中，$H_t={\Phi }^T{Q}_e\Phi +R_e，G_t=2E(t{)}^T{Q}_e\Phi ，P_t=E(t{)}^T{Q}_{e}E(t)，P_t$为常量，$Q_e,R_e$为权重矩阵$Q,R$的扩充矩阵。
结合mpc_slover.cc中的代码，

// Initialize matrix_k, matrix_m, matrix_t and matrix_v, matrix_qq, matrix_rr,
  // vector of matrix A power
  Matrix matrix_m = Matrix::Zero(matrix_b.rows() * horizon, 1);      // 60*1
  Matrix matrix_qq = Matrix::Zero(matrix_k.rows(), matrix_k.rows()); // 60*60
  Matrix matrix_rr = Matrix::Zero(matrix_k.cols(), matrix_k.cols()); // 20*20
  Matrix matrix_ll = Matrix::Zero(horizon * matrix_lower.rows(), 1); //20*1
  Matrix matrix_uu = Matrix::Zero(horizon * matrix_upper.rows(), 1); //20*1
  ...
  // Update matrix_m1, matrix_m2, convert MPC problem to QP problem done
  Matrix matrix_m1 = matrix_k.transpose() * matrix_qq * matrix_k + matrix_rr;
  Matrix matrix_m2 = matrix_k.transpose() * matrix_qq * (matrix_m - matrix_t);
  ...
  // TODO(QiL) : change qp solver to box constraint or substitute QPOASES
  // Method 1: QPOASES
  Matrix matrix_inequality_constrain_ll =
      Matrix::Identity(matrix_ll.rows(), matrix_ll.rows());
  ...
  // 求解
  std::unique_ptr<QpSolver> qp_solver(new ActiveSetQpSolver(
      matrix_m1, matrix_m2, matrix_inequality_constrain,
      matrix_inequality_boundary, matrix_equality_constrain,
      matrix_equality_boundary));
  auto result = qp_solver->Solve();

令$S=matrix\_initial\_state,M=matrix\_m,M1=matrix\_m1,M2=matrix\_m2,Q=matrix\_q,R=matrix\_r,QQ=matrix\_qq,RR=matrix\_rr,LL=matrix\_ll,UU=matrix\_uu$，根据代码有：
$$\begin{gathered} M=\left[\begin{array}{c}AS(t|t)+C\\ AM[0]+C\\ ⋮\\ AM[8]+C\end{array}\right]=\left[\begin{array}{c}AS(t|t)+C\\ A^{2}S(t|t)+AC+C\\ ⋮\\ A^{10}S(t|t)+{\sum }_{i=0}^9{A}^{i}C\end{array}\right], \\ QQ=\left[\begin{array}{cccc}Q& 0& \cdots & 0\\ 0& Q& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & Q\end{array}\right],RR=\left[\begin{array}{cccc}R& 0& \cdots & 0\\ 0& R& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & R\end{array}\right], \\ M1=K^T\ast QQ\ast K+RR=H_t,M2=K^T\ast QQ(M-Ref)=K^T\ast QQ\ast E(t)\text{\hspace{1em}(29)} \end{gathered}$$

因此，对模型预测控制的每一步进行带约束条件的优化问题，可转换为如下的二次规划问题：
$$\begin{gathered} \underset{\Delta U_t}{\min }\Delta U(t)H_t\Delta U(t{)}^T+G_t\Delta U(t{)}^T \\ \Delta U_{min}\le \Delta U_t(k)\le \Delta U_{max} \\ {U}_{min}\le u(t-1)+\sum _{i=1}^N\Delta U(i)\le U_{max} \\ {Y}_{min}\le {\Psi }_t\xi (t|t)+{\Phi }_t\Delta U(t|t)+{{\rm Y}}_t\le Y_{max}\text{\hspace{1em}(30)} \end{gathered}$$

此外，在mpc_slover.cc中有注释如下：

 // Update matrix_m1, matrix_m2, convert MPC problem to QP problem done

  // Format in qp_solver
  /**
   * *           min_x  : q(x) = 0.5 * x^T * Q * x  + x^T c
   * *           with respect to:  A * x = b (equality constraint)
   * *                             C * x >= d (inequality constraint)
   * **/
  // TODO(QiL) : change qp solver to box constraint or substitute QPOASES
  // Method 1: QPOASES

可知，Apollo将MPC的优化求解转化为二次规划(Quadratic Programming, QP)问题，且QP问题的求解采用QPOASES的方法，QPOASES方法详解请见：qpOASES: a parametric active-set algorithm for quadratic programming，可以结合active_set_qp_solver.cc以及矩阵计算库Eigen对QPOASES方法进行理解分析。

反馈矫正

2018.12.28更新
有博友提醒该步骤在Apollo代码中并未实现，我在学习的过程中，确实在Apollo代码中没有特别清晰的对应上这一步，可能是我理解的不够深吧。
但该步骤是我在参考书中看到的MPC求解的一般步骤，所以在此处我也写了。辩证地看待吧，我尽量保证我写的内容没有什么原则性的错误，感谢各位博友的提点和支持。

在每个控制周期内，按照公式30完成优化求解后，得到控制时域内的一系列控制增量：
$$\Delta U_t^{\ast }=[\Delta u_t^{\ast },\Delta u_{t+1}^{\ast },...,\Delta u_{t+N-1}^{\ast }]\text{\hspace{1em}(31)}$$
将序列中的第一个控制增量作为实际的控制输入增量作用于系统，则有：
$$u(t)=u(t-1)+\Delta u_t^{\ast }\text{\hspace{1em}(32)}$$
将$u(t)$作为此时的控制量输入给系统，直到下一个控制时刻，系统根据新的状态信息预测下一时段内的输出，然后通过优化得到一组新的控制序列。如此反复，直至完成整个控制过程。

总结

综上所述，MPC控制器的工作原理大致如下所示：

图4 MPC控制原理框图

其中，$x(t)$为$t$时刻车辆的观测状态，$\widehat{x(t)}$为$t$时刻车辆的估计状态，$u^{\ast }(t)$为t时刻的最优控制解，$y(t)$为$t$时刻的系统输出。

模型预测控制的实现，依赖MPC控制器、被控车辆、状态估计器、轨迹规划等信息。结合图1和图4，模型预测控制器的一般工作步骤可以概括如下：
1、在$t$时刻，结合历史信息和当前状态以及预测模型，预测$N$步的系统输出；
2、结合约束条件等，设计目标函数，计算最优控制解$u^{\ast }(t)$，输入到被控车辆，使其在当前控制量下运动；
3、获取车辆状态$x(t)$，输入到状态估计器中，对那些无法直接用传感器获取或观测成本较高的的状态量进行估计，然后将$\hat{x}(t)$输入到MPC控制器，再次进行优化求解，以得到未来一段时间的预测控制序列；
4、然后在$t+1$时刻重复上述步骤，如此，滚动地实现带约束的优化问题，从而实现对被控对象的连续控制。
此外，$x(t)$也可在需要的时候，被用来更新规划轨迹，以便得到更好的控制效果。

---

1. 无人驾驶汽车系统入门（十）——基于运动学模型的模型预测控制 ↩︎

2. 龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京理工大学出版社, 2014. ↩︎ ↩︎ ↩︎