基于apollo MPC、apollo LQR、PP(纯跟踪）算法的车辆路径跟踪控制对比仿真【附说明文档】 附带一

基于Apollo MPC、Apollo LQR、PP算法的车辆路径跟踪控制对比仿真

一、说明文档

本文档旨在详细分析、仿真并对比基于Apollo MPC、Apollo LQR以及PP算法的车辆路径跟踪控制。我们将从汽车动力学模型、方向盘控制模型、横纵控制状态变量、预测状态模型分析以及算法效果分析等方面进行详细阐述。

二、理论分析

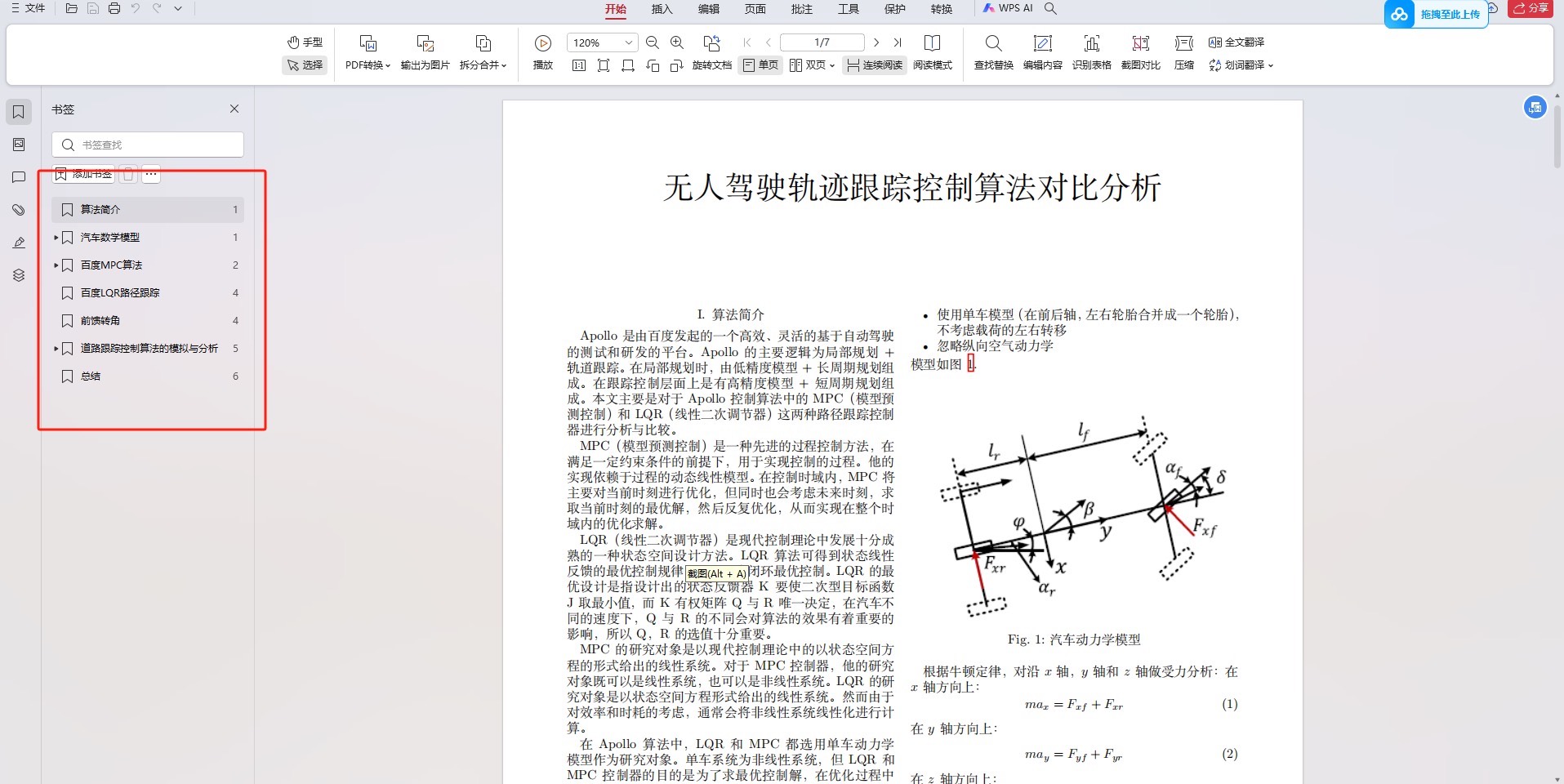
1. 汽车动力学模型

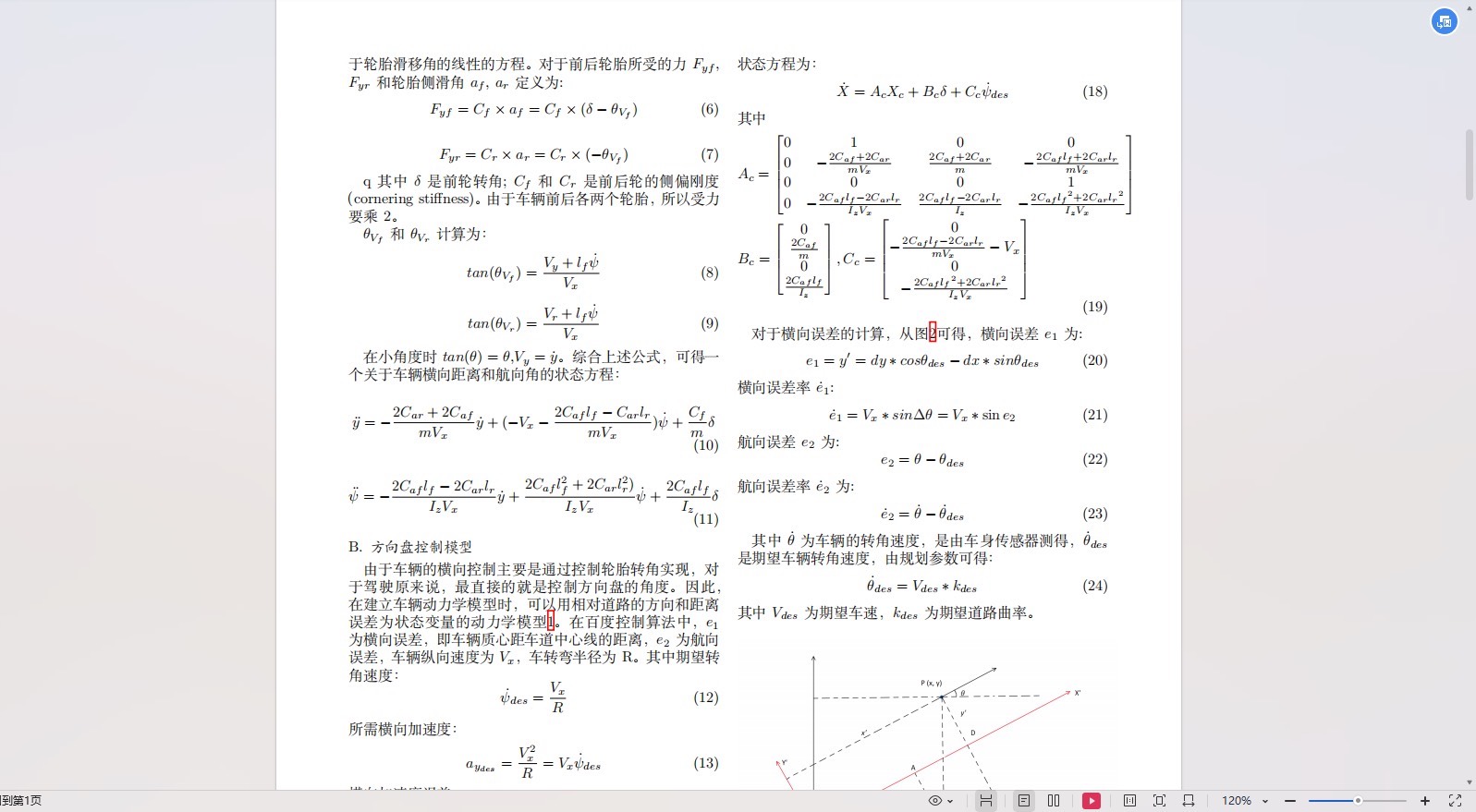
汽车动力学模型是路径跟踪控制的基础。考虑到车辆的运动学特性，我们将采用二自由度模型，即纵向速度和横向位置作为控制目标。

2. 方向盘控制模型

方向盘控制模型基于转向角度和车速，通过计算得出合适的转向角度，以实现车辆的路径跟踪。

3. 横纵控制状态变量

横纵控制状态变量包括车辆的横向位置、纵向速度以及方向盘角度等，这些变量将用于评估和控制车辆的路径跟踪效果。

三、仿真搭建

1. 仿真环境设定

模拟的赛道由直道和弯道组成，无障碍物。车辆从距离赛道原点横向两米的位置为起点开始仿真。

2. 算法实现

分别实现Apollo MPC、Apollo LQR和PP算法，并集成到仿真环境中。

四、仿真分析

1. 预测状态模型分析

对于MPC和LQR算法，我们需要构建预测模型以预测车辆未来的状态。这些模型将基于汽车动力学模型和方向盘控制模型进行构建。对于PP算法，其预测是基于几何关系的纯跟踪算法。

2. 算法效果分析

在仿真过程中，我们将分别记录三种算法的路径跟踪效果，包括跟踪误差、跟踪速度等指标。通过对这些指标的分析，我们可以评估每种算法的优劣。

五、三种算法对比

1. Apollo MPC横纵向模型预测控制

MPC通过构建一个优化问题，来找到最优的控制输入以最小化跟踪误差。其优点在于能够考虑未来的状态和约束，从而实现更平滑的路径跟踪。

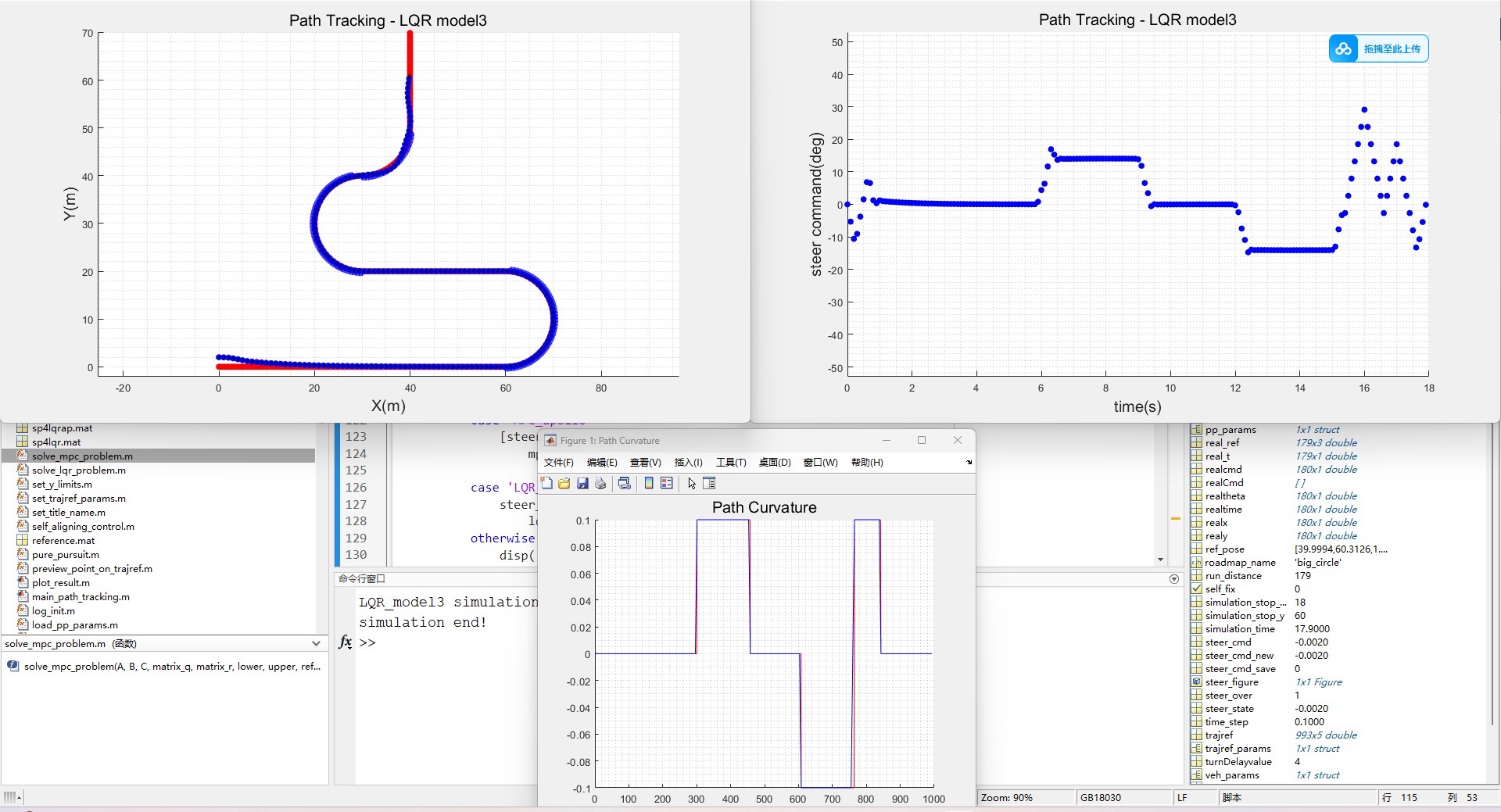
2. Apollo LQR横向路径跟踪控制

LQR通过线性化模型并设计一个线性反馈控制器来实现路径跟踪。其优点在于计算简单，但可能对非线性的适应性较差。

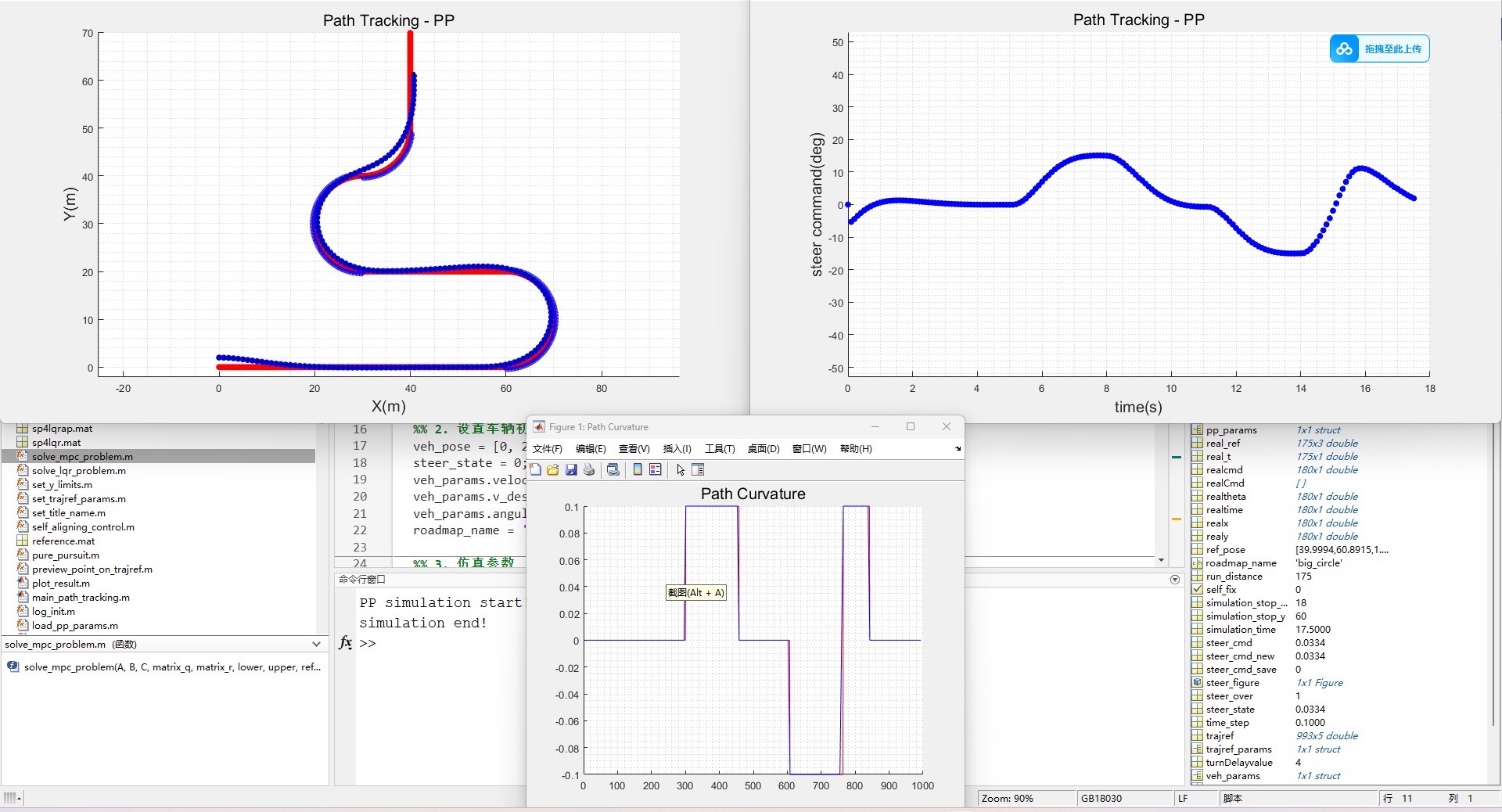
3. PP算法路径跟踪控制

PP算法基于纯跟踪几何关系进行路径跟踪。其优点在于简单易实现，但在复杂环境下可能存在跟踪误差较大的问题。

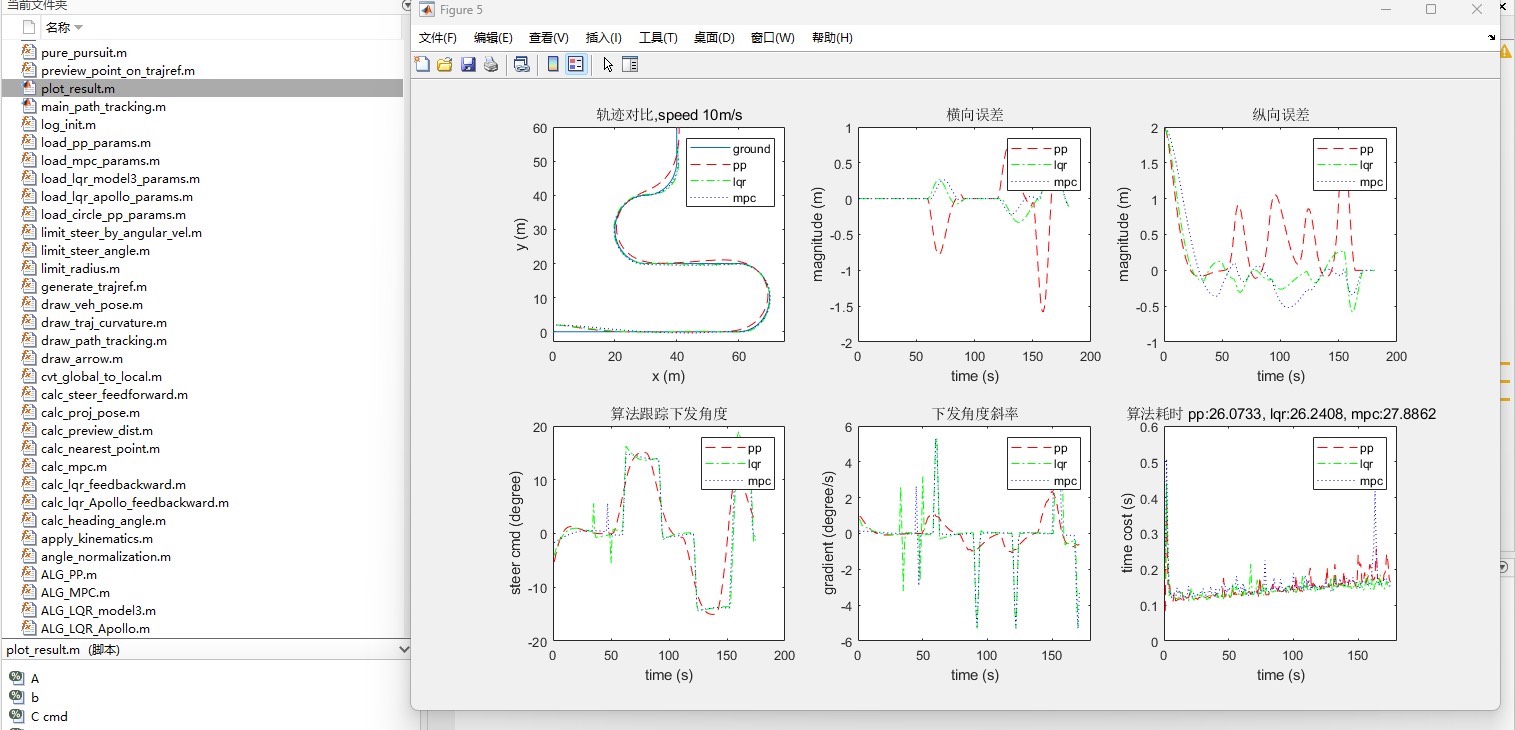
六、模拟结果与讨论

我们将对比三种算法的模拟结果，分析其各自的优缺点，并讨论在实际情况中如何选择合适的算法。同时，我们将提供程序附带中文注释，以便于学习理解。如有需要，我们还可以提供付费讲解指导服务。

七、总结与展望

本文对基于Apollo MPC、Apollo LQR和PP算法的车辆路径跟踪控制进行了详细的对比分析。未来，我们还将继续研究更先进的算法，以提高车辆的路径跟踪性能和安全性。
基于apollo MPC、apollo LQR、PP(纯跟踪）算法的车辆路径跟踪控制对比仿真【附说明文档】
附带一份详细理论分析、仿真搭建、仿真分析说明文档
内容：汽车动力学模型、方向盘控制模型、横纵控制状态变量、预测状态模型分析、算法效果分析
三种算法对比:
①MPC横纵向模型预测控制
②LQR横向路径跟踪控制
③PP算法路径跟踪控制
算法的对比：PP, Apollo LQR, Apollo MPC。
模拟的环境是一个没有障碍物的赛道，赛道由直道和弯道组合而成。
车辆会先从距离赛道原点横向两米的位置为起点，向预定道路靠拢。
模拟的目标是为了让汽车成功尽可能的平滑
和正确的跟随给定轨迹到达终点。
程序附带中文注释便于学习可以提供付费讲解指导服务。