无需归一化的 Transformer（何凯明，LeCun) CVPR 2025

Project: Transformers without Normalization - DynamicTanh - DyT

arxiv

Abstract

Normalization layers are ubiquitous in modern neural networks and have long been considered essential. ​This work demonstrates that Transformers without normalization can achieve the same or better performance using a remarkably simple technique. We introduce ​Dynamic Tanh (DyT), an element-wise operation ​DyT(x) = tanh(αx), as a ​drop-in replacement for normalization layers in Transformers. ​DyT is inspired by the observation that layer normalization in Transformers often produces tanh-like, S-shaped input-output mappings. By incorporating ​DyT, ​Transformers without normalization can match or exceed the performance of their normalized counterparts, mostly without hyperparameter tuning. We validate the effectiveness of ​Transformers with DyT across diverse settings, ranging from ​recognition to generation, ​supervised to self-supervised learning, and ​computer vision to language models. ​These findings challenge the conventional understanding that normalization layers are indispensable in modern neural networks, and offer new insights into their role in deep networks.

标准化层在现代神经网络中无处不在，长期以来被认为是必不可少的。​这项工作表明，通过一种极其简单的技术，无需标准化的Transformer可以实现相同甚至更好的性能。​ 作者引入了动态Tanh（DyT）​，这是一种逐元素操作DyT(x) = tanh(αx)，作为Transformer中标准化层的直接替代品。​DyT的灵感来自于观察发现，Transformer中的层标准化（Layer Normalization, LN）通常会产生类似Tanh的S形输入-输出映射。​ 通过引入DyT，​无需标准化的Transformer可以在大多数情况下无需超参数调整的情况下，匹配或超越其标准化版本的表现。​ 本文在多种场景下验证了基于DyT的Transformer的有效性，包括从识别到生成、监督学习到自监督学习，以及从计算机视觉到语言模型。​这些发现挑战了传统观念，即标准化层在现代神经网络中是不可或缺的，并为它们在深度网络中的作用提供了新的见解。​

Introduction

Over the past decade, ​normalization layers have solidified their positions as one of the most fundamental components of modern neural networks. It all traces back to the invention of ​batch normalization in 2015 (Ioffe and Szegedy, 2015), which enabled drastically faster and better convergence in visual recognition models and quickly gained momentum in the following years. Since then, many variants of ​normalization layers have been proposed for different network architectures or domains (Ba et al., 2016; Ulyanov et al., 2016; Wu and He, 2018; Zhang and Sennrich, 2019). Today, virtually all modern networks use ​normalization layers, with ​layer normalization (Layer Norm, or LN) (Ba et al., 2016) being one of the most popular, particularly in the dominant ​Transformer architecture (Vaswani et al., 2017; Dosovitskiy et al., 2020).

背景

在过去十年中，​标准化层已经巩固了其作为现代神经网络中最基本组件之一的地位。这一切可以追溯到2015年批量标准化（Batch Normalization）​的发明，它使得视觉识别模型的收敛速度显著加快且效果更好，并在随后的几年中迅速普及。自那时起，针对不同网络架构或领域的多种标准化层变体被提出。如今，几乎所有现代网络都使用标准化层，其中层标准化（Layer Norm, LN）是最受欢迎的之一，尤其是在主流的Transformer架构中。

The widespread adoption of normalization layers is largely driven by their empirical benefits in optimization (Santurkar et al., 2018; Bjorck et al., 2018). In addition to achieving better results, they help accelerate and stabilize convergence. As neural networks become wider and deeper, this necessity becomes ever more critical (Brock et al., 2021a; Huang et al., 2023). Consequently, ​normalization layers are widely regarded as crucial, if not indispensable, for the effective training of deep networks. This belief is subtly evidenced by the fact that, in recent years, novel architectures often seek to replace ​attention or convolution layers (Tolstikhin et al., 2021; Gu and Dao, 2023; Sun et al., 2024; Feng et al., 2024), but almost always retain the ​normalization layers.

问题

标准化层的广泛采用主要归功于其在优化中的实证优势。除了实现更好的结果外，它们还有助于加速和稳定收敛。随着神经网络变得越来越宽和越来越深，这种必要性变得愈发关键。因此，​标准化层被广泛认为是深度网络有效训练的关键，甚至不可或缺。​这一信念在近年来得到了微妙体现：尽管新型架构常常试图替换注意力或卷积层​，但几乎总是保留标准化层。

This paper challenges this belief by introducing a simple alternative to normalization layers in Transformers. Our exploration starts with the observation that ​LN layers map their inputs to outputs with tanh-like, S-shaped curves, scaling the input activations while squashing the extreme values. Inspired by this insight, we propose an element-wise operation termed ​Dynamic Tanh (DyT), defined as: ​DyT(x) = tanh(αx), where ​α is a learnable parameter. This operation aims to emulate the behavior of ​LN by learning an appropriate scaling factor through ​α and squashing extreme values via the bounded ​tanh function. Notably, unlike ​normalization layers, it achieves both effects ​without the need to compute activation statistics.

方法

本文通过引入一种简单的替代方案，挑战了这一信念。​ 本文的探索始于观察到LN层将其输入映射为类似Tanh的S形曲线输出，在缩放输入激活值的同时压缩极端值。受此启发，本提出了一种逐元素操作，称为动态Tanh（DyT）​，其定义为：​DyT(x) = tanh(αx)，其中α是一个可学习参数。​该操作旨在通过α学习适当的缩放因子，并通过有界的Tanh函数压缩极端值，从而模拟LN的行为。​ 值得注意的是，与标准化层不同，它无需计算激活统计量即可实现这两种效果。

Employing DyT is straightforward, as shown in Figure 1: we directly replace existing ​normalization layers with ​DyT in architectures such as ​vision and language Transformers. We empirically demonstrate that models with ​DyT can train stably and achieve high final performance across a wide range of settings. It often does not require tuning the training hyperparameters on the original architecture. ​Our work challenges the notion that normalization layers are indispensable for training modern neural networks and provides empirical insights into the properties of normalization layers. Moreover, preliminary measurements suggest that ​DyT improves training and inference speed, making it a candidate for ​efficiency-oriented network design.

Figure 1 Left: original Transformer block. Right: block with our proposed Dynamic Tanh (DyT) layer. DyT is a straightforward replacement for commonly used Layer Norm (Ba et al., 2016) (in some cases RMSNorm (Zhang and Sennrich, 2019)) layers. Transformers with DyT match or exceed the performance of their normalized counterparts.

结果

使用DyT非常简单，如图1所示：本文直接在诸如视觉和语言Transformer的架构中用DyT替换现有的标准化层。​通过实验证明，基于DyT的模型可以在各种设置下稳定训练并实现较高的最终性能，且通常无需调整原始架构的训练超参数。​ ​本文的工作挑战了标准化层在训练现代神经网络中不可或缺的观念，并为标准化层的性质提供了实证见解。​ 此外，初步测量表明，​DyT提高了训练和推理速度，使其成为高效网络设计的候选方案。

---

Background: Normalization Layers

首先回顾标准化层。大多数标准化层共享一个共同的公式。给定形状为 (B, T, C) 的输入 x，其中 B 是批量大小，T 是 token 数量，C 是每个 token 的嵌入维度，输出通常计算为：

标准化(x) = γ ∗ ( (x − µ) / √(σ² + ϵ) ) + β​

其中，ϵ 是一个小的常数，γ 和 β 是形状为 (C,) 的可学习向量参数。它们是“缩放”和“平移”的仿射参数，允许输出处于任何范围。µ 和 σ² 分别表示输入的均值和方差。不同方法的主要区别在于如何计算这两个统计量，这导致 µ 和 σ² 具有不同的维度，并且在计算过程中应用广播。

批量标准化（BN）是第一个现代标准化层，主要用于卷积网络（ConvNet）模型。它的引入代表了深度学习架构设计的一个重要里程碑。BN 在批次和 token 维度上计算均值和方差，具体为： 和 。

其他在卷积网络中流行的标准化层，例如组标准化（Group Normalization）​​和实例标准化（Instance Normalization）​​，最初是为目标检测和图像风格化等专门任务提出的。它们共享相同的总体公式，但在计算统计量的轴和范围上有所不同。

层标准化（LN）​​和均方根标准化（RMSNorm）​​是 Transformer 架构中使用的两种主要标准化层。LN 为每个样本中的每个 token 独立计算这些统计量，其中和 。RMSNorm通过移除均值中心化步骤简化了 LN，并使用对输入进行标准化。如今，大多数现代神经网络使用 LN，因为它简单且通用。最近，RMSNorm 越来越受欢迎，特别是在 T5、LLaMA、Mistral、Qwen、InternLM和 DeepSeek等语言模型中。本文在这项工作中研究的 Transformer 都使用 LN，除了 LLaMA 使用 RMSNorm。

---

What Do Normalization Layers Do?

Analysis setup.

We first empirically study the behaviors of ​normalization layers in trained networks. For this analysis, we take a ​Vision Transformer model (ViT-B) (Dosovitskiy et al., 2020) trained on ​ImageNet-1K (Deng et al., 2009), a ​wav2vec 2.0 Large Transformer model (Baevski et al., 2020) trained on ​LibriSpeech (Panayotov et al., 2015), and a ​Diffusion Transformer (DiT-XL) (Peebles and Xie, 2023) trained on ​ImageNet-1K. In all cases, ​Layer Normalization (LN) is applied in every ​Transformer block and before the final ​linear projection.

For all three trained networks, we sample a mini-batch of samples and do a ​forward pass through the network. We then measure the ​input and output for the ​normalization layers, i.e., tensors immediately before and after the ​normalization operation, before the ​learnable affine transformation. Since ​LN preserves the dimensions of the input tensor, we can establish a ​one-to-one correspondence between the input and output tensor elements, allowing for a direct visualization of their relationship. We plot the resulting mappings in ​Figure 2.

标准化层的作用是什么？

分析设置

本文首先对训练好的网络中的标准化层行为进行了实证研究。为此，作者选择了在ImageNet-1K​上训练的Vision Transformer模型（ViT-B）、在LibriSpeech​上训练的wav2vec 2.0 Large Transformer模型​，以及在ImageNet-1K上训练的Diffusion Transformer（DiT-XL）。在所有情况下，​层标准化（LN）​都应用于每个Transformer模块以及最终的线性投影之前。

对于这三个训练好的网络，采样了一个小批量样本并进行了前向传播。然后，测量了标准化层的输入和输出，即在标准化操作之前和之后的张量，以及在可学习的仿射变换之前。由于LN保留了输入张量的维度，可以在输入和输出张量元素之间建立一一对应关系，从而直接可视化它们的关系。将结果映射绘制在图2中。

Tanh-like mappings with layer normalization.

For all three models, in earlier ​LN layers (1st column of Figure 2), we find this ​input-output relationship to be mostly linear, resembling a straight line in an x-y plot. However, the deeper ​LN layers are places where we make more intriguing observations.

Figure 2 Output vs. input of selected layer normalization (LN) layers in Vision Transformer (ViT) (Dosovitskiy et al., 2020), wav2vec 2.0 (a Transformer model for speech) (Baevski et al., 2020), and Diffusion Transformer (DiT) (Peebles and Xie, 2023). We sample a mini-batch of samples and plot the input / output values of four LN layers in each model. The outputs are before the affine transformation in LN. The S-shaped curves highly resemble that of a tanh function (see Figure 3). The more linear shapes in earlier layers can also be captured by the center part of a tanh curve. This motivates us to propose Dynamic Tanh (DyT) as a replacement, with a learnable scaler α to account for different scales on the x axis.

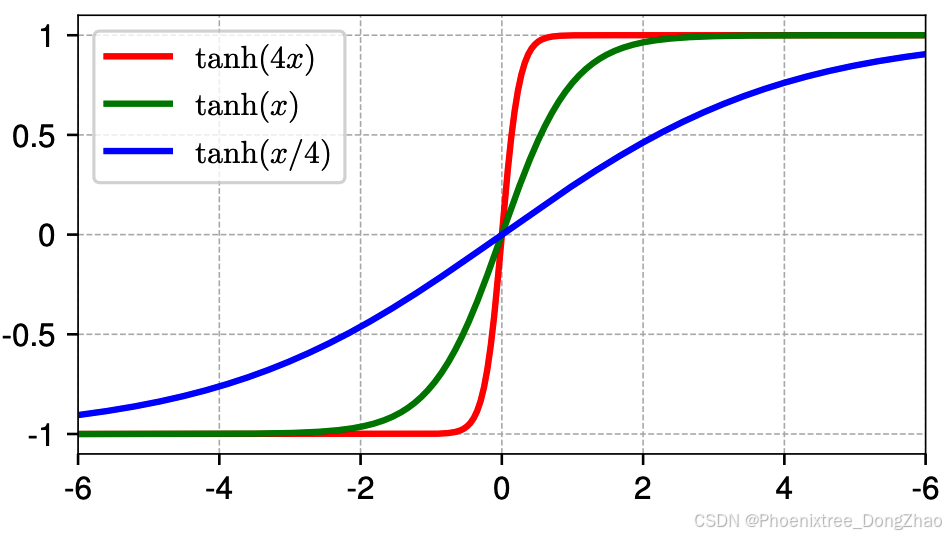
A striking observation from these deeper layers is that most of these curves’ shapes highly resemble full or partial ​S-shaped curves represented by a ​tanh function (see ​Figure 3). One might expect ​LN layers to linearly transform the input tensor, as subtracting the mean and dividing by standard deviation are ​linear operations. ​LN normalizes in a ​per-token manner, only linearly transforming each token’s activations. As tokens have different mean and standard deviation values, the linearity does not hold collectively on all activations of the input tensor. Nonetheless, it is still surprising to us that the actual ​non-linear transformation is highly similar to a scaled ​tanh function.

Figure 3 tanh(αx) with three different α values.

类似Tanh的层标准化映射

对于所有三个模型，在早期的LN层​（图2的第一列）中，作者发现输入-输出关系大多是线性的，类似于x-y图中的一条直线。然而，在更深的LN层中，观察到了一些更有趣的现象。

从这些深层中，一个引人注目的观察是，这些曲线的形状与Tanh函数所代表的完整或部分S形曲线高度相似（参见图3）。人们可能会期望LN层对输入张量进行线性变换，因为减去均值并除以标准差是线性操作。​LN以逐token的方式进行标准化，仅对每个token的激活值进行线性变换。由于token具有不同的均值和标准差，线性性并不适用于输入张量的所有激活值。尽管如此，本文仍然惊讶地发现，实际的非线性变换与缩放的Tanh函数高度相似。

For such an ​S-shaped curve, we note that the central part, represented by points with x values close to zero, is still mainly in a ​linear shape. Most points (∼99%) fall in this linear range. However, there are still many points that clearly fall out of this range, which are considered to have ​​“extreme” values, e.g., those with x larger than 50 or smaller than -50 in the ​ViT model. ​Normalization layers’ main effect for these values is to squash them into less extreme values, more in line with the majority of points. This is where ​normalization layers could not be approximated by a simple ​affine transformation layer. ​We hypothesize this non-linear and disproportional squashing effect on extreme values is what makes normalization layers important and indispensable.

Recent findings by Ni et al. (2024) similarly highlight the ​strong non-linearities introduced by ​LN layers, demonstrating how the ​non-linearity enhances a model’s ​representational capacity. Moreover, this ​squashing behavior mirrors the ​saturation properties of biological neurons for large inputs, a phenomenon first observed about a century ago (Adrian, 1926; Adrian and Zotterman, 1926a,b).

对于这样的S形曲线，作者注意到，以x值接近零的点为代表的中心部分仍然主要是线性形状。大多数点（约99%）落在这个线性范围内。然而，仍有许多点明显超出了这个范围，这些点被认为是具有​“极端”值，例如在ViT模型中x大于50或小于-50的点。​标准化层对这些值的主要作用是将它们压缩为不太极端的值，使其更符合大多数点的范围。​正是在这一点上，标准化层无法通过简单的仿射变换层来近似。作者假设，这种对极端值的非线性和不成比例的压缩效应是标准化层重要且不可或缺的原因。​

最近Ni等人（2024）的研究同样强调了LN层引入的强非线性，展示了非线性如何增强模型的表示能力。此外，这种压缩行为反映了生物神经元对大量输入的饱和特性，这一现象最早在一个世纪前被观察到（Adrian, 1926; Adrian和Zotterman, 1926a,b）。

Normalization by tokens and channels.

How does an ​LN layer perform a ​linear transformation for each token but also squash the ​extreme values in such a ​non-linear fashion? To understand this, we visualize the points grouped by ​tokens and channels, respectively. This is plotted in ​Figure 4 by taking the second and third subplots for ​ViT from ​Figure 2, but with a sampled subset of points for more clarity. When we select the channels to plot, we make sure to include the channels with ​extreme values.

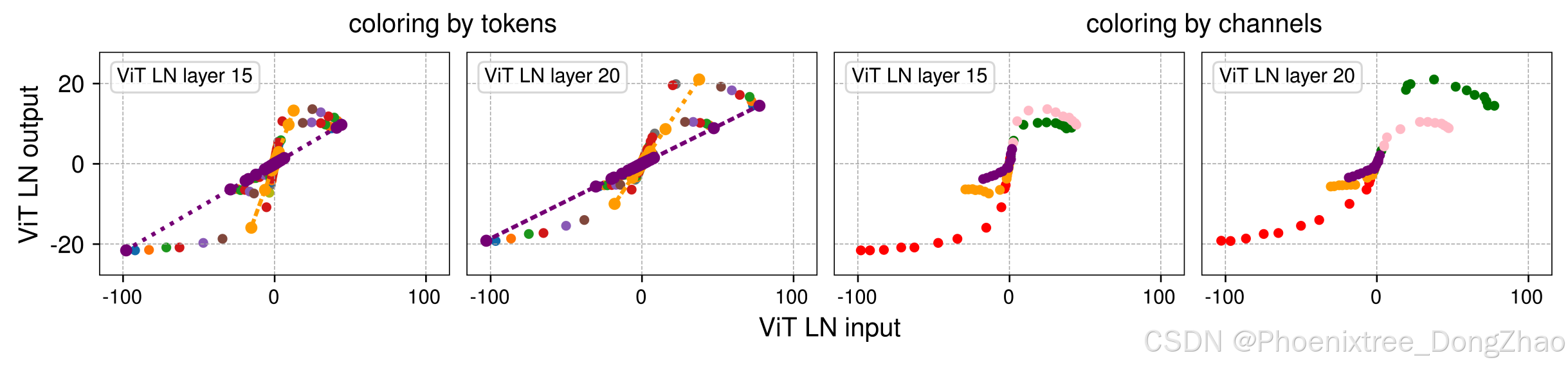
Figure 4. Output vs. input of two ​LN layers, with tensor elements colored to indicate different ​channel and token dimensions. The input tensor has a shape of (samples, tokens, and channels), with elements visualized by assigning consistent colors to the same tokens (left two panels) and channels (right two panels). ​Left two panels: points representing the same token (same color) form straight lines across different channels, as ​LN operates linearly across channels for each token. Interestingly, when plotted collectively, these lines form a ​non-linear tanh-shaped curve. ​Right two panels: each channel’s input spans different ranges on the x-axis, contributing distinct segments to the overall ​tanh-shaped curve. Certain channels (e.g., red, green, and pink) exhibit more ​extreme x values, which are squashed by ​LN.

On the left two panels of ​Figure 4, we visualize each token’s activations using the same color. We observe that all points from any single token do form a ​straight line. However, since each token has a different variance, the slopes are different. Tokens with smaller input x ranges tend to have smaller variance, and the ​normalization layer will divide their activations using a smaller standard deviation, hence producing a larger slope in the straight line. Collectively, they form an ​S-shaped curve that resembles a ​tanh function. In the two panels on the right, we color each channel’s activations using the same color. We find that different channels tend to have drastically different input ranges, with only a few channels (e.g., red, green, and pink) exhibiting large ​extreme values. These are the channels that get squashed the most by the ​normalization layer.

按token和通道的标准化

LN层如何对每个token执行线性变换，同时以这种非线性方式压缩极端值？为了理解这一点，本文分别按token和通道对点进行可视化。这在图4中通过从图2中提取ViT的第二和第三子图进行绘制，但为了更清晰，使用了采样的点子集。在选择要绘制的通道时，确保包含具有极端值的通道。

在图4的左侧两个面板中，使用相同颜色可视化每个token的激活值。可以观察到，来自任何一个token的所有点确实形成了一条直线。然而，由于每个token的方差不同，斜率也不同。输入x范围较小的token往往具有较小的方差，​标准化层会使用较小的标准差来划分它们的激活值，从而在直线中产生较大的斜率。总体而言，它们形成了一条S形曲线，类似于Tanh函数。在右侧的两个面板中，使用相同颜色对每个通道的激活值进行着色。作者发现，不同通道的输入范围往往差异很大，只有少数通道（例如红色、绿色和粉色）表现出较大的极端值。这些是标准化层压缩最多的通道。

---

Dynamic Tanh (DyT)

Inspired by the similarity between the shapes of ​normalization layers and a scaled ​tanh function, we propose ​Dynamic Tanh (DyT) as a ​drop-in replacement for ​normalization layers. Given an input tensor x, a ​DyT layer is defined as follows:

DyT(x) = γ ∗ tanh(αx) + β (2)

where ​α is a ​learnable scalar parameter that allows scaling the input differently based on its range, accounting for varying x scales (Figure 2). This is also why we name the whole operation ​​“Dynamic” Tanh. ​γ and ​β are ​learnable, per-channel vector parameters, the same as those used in all ​normalization layers—they allow the output to scale back to any scales. This is sometimes considered a separate ​affine layer; for our purposes, we consider them to be part of the ​DyT layer, just like how ​normalization layers also include them. See ​Algorithm 1 for implementation of ​DyT in Pytorch-like pseudocode.

Integrating DyT layers into an existing architecture is straightforward: one ​DyT layer replaces one ​normalization layer (see ​Figure 1). This applies to ​normalization layers within ​attention blocks, ​FFN blocks, and the final ​normalization layer. Although ​DyT may look like or be considered an ​activation function, this study only uses it to replace ​normalization layers without altering any parts of the ​activation functions in the original architectures, such as ​GELU or ​ReLU. Other parts of the networks also remain intact. We also observe that there is little need to tune the ​hyperparameters used by the original architectures for ​DyT to perform well.

动态Tanh（DyT）​

受标准化层的形状与缩放Tanh函数相似性的启发，本文提出了动态Tanh（DyT）​作为标准化层的直接替代品。给定输入张量x，​DyT层定义如下：

DyT(x) = γ ∗ tanh(αx) + β​（公式2）

其中，​α是一个可学习的标量参数，它允许根据输入的范围对输入进行不同的缩放，以应对不同的x尺度（图2）。这也是本文将整个操作命名为​“动态”Tanh的原因。​γ和β是可学习的、逐通道的向量参数，与所有标准化层中使用的参数相同——它们允许输出缩放到任何尺度。这有时被视为一个单独的仿射层；在本文的用途中，将其视为DyT层的一部分，就像标准化层也包含它们一样。参见算法1，了解DyT在Pytorch风格伪代码中的实现。

将DyT层集成到现有架构中非常简单：一个DyT层替换一个标准化层​（参见图1）。这适用于注意力块、FFN块和最终标准化层中的标准化层。尽管DyT可能看起来或被视为一种激活函数，但本研究仅使用它来替换标准化层，而不改变原始架构中的激活函数部分，例如GELU或ReLU。网络的其他部分也保持不变。作者还观察到，​DyT通常无需调整原始架构的超参数即可表现良好。

On scaling parameters.

We always simply initialize ​γ to an ​all-one vector and ​β to an ​all-zero vector following ​normalization layers. For the ​scaler parameter α, a default initialization of ​0.5 is generally sufficient, except for ​LLM training. A detailed analysis of ​α initialization is provided in ​Section 7. Unless explicitly stated otherwise, ​α is initialized to ​0.5 in our subsequent experiments.

关于缩放参数

作者总是简单地将γ初始化为全1向量，将β初始化为全0向量，这与标准化层的做法一致。对于缩放参数α，默认初始化为0.5通常足够，除了LLM训练。关于α初始化的详细分析见第7节。除非另有说明，否则在后续实验中，​α初始化为0.5。

Remarks.

DyT is not a new type of ​normalization layer, as it operates on each input element from a tensor independently during a ​forward pass without computing ​statistics or other types of ​aggregations. It does, however, preserve the effect of ​normalization layers in squashing the ​extreme values in a ​non-linear fashion while almost ​linearly transforming the very central parts of the input.

备注

DyT并不是一种新的标准化层，因为它在前向传播期间独立地对张量中的每个输入元素进行操作，而无需计算统计量或其他类型的聚合。然而，它确实保留了标准化层的效果，以非线性方式压缩极端值，同时对输入的中心部分进行几乎线性变换。