概率空間

概率空間是概率論的基礎。概率的嚴格定義基于這個概念。

定義

概率空間(Ω, F, P)是一個總測度為1的測度空間（即P(Ω)=1）.

第一項Ω是一個非空集合，有時稱作“樣本空間”。Ω 的集合元素稱作“樣本輸出”，可寫作ω。

第二項F是樣本空間Ω的幂集的一個非空子集。F的集合元素稱為事件Σ。事件Σ是樣本空間Ω的集族。集合F必須是一個σ-代數：

1. ；
2. 若，則；
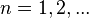3. 若，，則

(Ω, F)合起來稱為可测空間。事件就是樣本輸出的集合，在此集合上可定義其概率。

第三項P稱為概率，或者概率測度。這是一個從集合F到實數域R的函數，。每個事件都被此函數賦予一個0和1之間的概率值。P必須是一個測度，且P(Ω)=1。

概率測度經常以黑体表示，例如或，也可用符號"Pr"來表示。

例子

若樣本空間是關于一個机會均等的拋硬幣動作，則樣本輸出為“正面”或“反面”。事件為：

• {正面}，其概率為0.5。
• {反面}，其概率為0.5。
• { }=∅ 非正非反，其概率為0.
• {正面，反面}，不是正面就是反面，這是Ω，其概率為1。

相關概念

隨机變量

隨机變量是一個從Ω映射到另一個集合(通常是實數域R)的函數。 它必須是一個可测函數。比如說，若X是一個實隨机變量，則使X為正的樣本輸出的集合{ω∈Ω:X(ω)>0}是一個事件。

為簡便起見，{ω∈Ω:X(ω)>0}經常只寫作{X>0}。P({X>0})更被簡化為P(X>0)。

獨立

若P(A∩B)=P(A)P(B)，則A和B兩個事件是独立的。

若任何与隨机變量X有關的事件和任何与隨机變量Y有關的事件獨立，則X和Y兩個隨机變量是獨立的。

獨立這個概念是概率論和測度論分道扬镳的地方。

互斥

若P(A∩B)=0，则稱A和B兩個事件互斥或不相交（這個性質要比A∩B=∅弱一些，后者是集合不相交的定義）。

若兩個事件A和B不相交，則P(A∪B)=P(A)+P(B)。這個性質可以擴展到由（有限個或者可數無限個）事件組成的事件序列。 但不可數無限個事件組成的事件集合對應的概率与集合元素對應概率之和未必相等，例如若Z是正態分佈的隨机變量，則對任意x有P(Z=x)=0，但是P(Z是實數)=1。

事件A∩B的意思是A并且B；事件A∪B的意思是A或者B.