什么是GCN
- Graph Convolutional Networks,图卷积神经网络,实际上跟CNN一样,就是一个特征提取器,只不过它的对象是图数据。
- GCN就精妙的设计了一种从图数据中提取特征的方法,从而让我们可以使用这些特征去对图数据及逆行处理:
- 节点分类(node classification)
- 图分类(graph classification)
- 边预测(link prediction)
- 图嵌入表示(graph embedding)
- GCN应用已经渗透在CV,NLP,RS中

GCN算法的优势
- 具有可扩展的优点,能够适应网络的变化
- 相较于起传统的深度学习,图神经网络由于在关系数据挖掘方面有巨大的潜力,正成为学术界和工业界投入研发的热点,比如商品推荐,金融风控,聊天机器人中的语义分析及意图识别
GCN算法原理
在进行GCN算法之前,我们首先得有一张图,对于一个图网络G=(V,E),有N个节点,每个节点都有自己的特征,目标是要学习图上的信号或特征的一个映射。

-
其次我们对这张图求出它的邻接矩阵,这个邻接矩阵的每一行/每一列对应每一个节点,矩阵中的数字1代表两两节点之间存在边的关系,而数字0则代表没有边的关系。

-
然后我们还有度矩阵,度矩阵的表达方式是在对角线上显示每个节点的度的数量(即边的数量),比如:
- 在节点1中,有节点5+节点2与其相连,那么节点1的度为2。
- 在节点2中,有节点5+节点1+节点3与其相连,那么节点2的度为3。
-
有了邻接矩阵和度矩阵,我们可以通过以下公式,求出拉普拉斯矩阵:
L = D − A L 表 示 拉 普 拉 斯 矩 阵 D 为 节 点 矩 阵 A 为 邻 接 矩 阵 L = D - A\\ L表示拉普拉斯矩阵\\ D为节点矩阵\\ A为邻接矩阵 L=D−AL表示拉普拉斯矩阵D为节点矩阵A为邻接矩阵

-对于常见的拉普拉斯矩阵,除了有L=D-A的形式,还有以下两种:
L s y s = D − 1 2 A D − 1 2 L r w = D − 1 A L^{sys} = D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\\ L^{rw} = D^{-1}A Lsys=D−21AD−21Lrw=D−1A
使用拉普拉斯矩阵的好处有以下三点: -
拉普拉斯是对称矩阵,可以进行特征的分解(谱分解)
-
只有在中心顶点和一阶相连的顶点上(1-hop neighbor)有非0元素,其余之处均为0
-
通过拉普拉斯算子与拉普拉斯矩阵进行类比
当有了以上的矩阵和算子,那么便可以进行GCN的转换了。
GCN模型的输入为矩阵X和A:
- 矩阵X,表示这些节点特征,N×D维矩阵
- 矩阵A,表示各个节点之间的关系,N×N维矩阵,也称为邻接矩阵(adjacency matrix)
GCN是一个神经网络层,层与层之间的传播方式:


公式解释:
- 每一层GCN的输入都是邻接矩阵A和Node的特征H,如果我们直接做一个内积,乘以一个参数矩阵W,再激活一下,就相当于一个简单的神经网络层
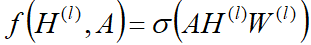
实验证明,使用这个简单的神经网络层,就已经很强大了
不过这个简单模型有2个局限性:
- 局限1,只使用A的话,由于A的对角线上都是0,所以在和特征矩阵H相乘的时候,只会计算一个node的所有邻居的特征的加权和,该node本身的特征却被忽略了。
- 那么便可以针对此做一个小的变动,即给A加上一个单位矩阵I,这样就让对角线元素变成1了。
- 局限2,A是没有经过归一化的矩阵,如果A与特征矩阵H相乘会改变特征原本的分布,产生一些不可预测的问题。
- 所以我们可以对A做一个标准化的处理,首先让A的每一行加起来为1,然后对A乘以D^-1,D为度矩阵,那么便可以解决局限2。
- 进一步把D^-1拆开与A相乘,得到一个对称且归一化的矩阵:
D − 1 2 A D − 1 2 D^{-\frac{1}{2}}A D^{-\frac{1}{2}} D−21AD−21 - 综合以上两种改进方式,得到:

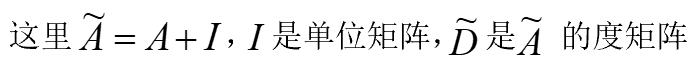


























 949
949

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










