设三相3个标量分别为,且满足
,可引入变换
(1)
其中,式(1)中将3个标量
用一个复数表示,复数
在复平面上为一个向量。由欧拉方程
得
将带入(1)式得:
(2)
如下图所示,实部和虚部分别表示为
(3)
(4)
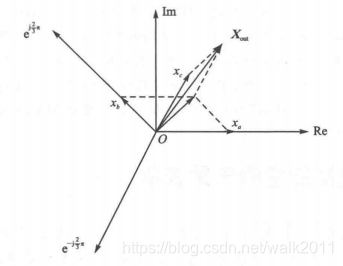
将(3)(4)式与并联得
如果复数已知,则可以求出唯一
,即
这样,就将3个标量使用一个复数
表示
假设三相正弦对称电压瞬间值表示为
其中为相电压的幅值,
为角频率,三相相电压
对应的空间电压矢量为
根据(3)(4)求得电压矢量的实部和虚部分别为
(5)
(6)
由三角函数中二角和差公式
得
根据(5)(6)得电压矢量的实部和虚部为
故电压空间矢量为
(7)
























 4753
4753

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








