前言
若三角形的四心用文字语言表述时,许多学生还可以对付一阵,若但换成向量形式的符号语言,则大多就哑口无言了,所以有必要将三角形四心的向量表示形式好好作以总结储备。 相关延伸
常用结论
1、已知 O O O 为 △ A B C \triangle ABC △ABC内的一点,若 O A → \overrightarrow{OA} OA + + + O B → \overrightarrow{OB} OB + + + O C → \overrightarrow{OC} OC = = = 0 ⃗ \vec{0} 0,则 O O O 是 △ A B C \triangle ABC △ABC的重心;
2、已知 O O O 为 △ A B C \triangle ABC △ABC内的一点,满足 ∣ O A → ∣ = ∣ O B → ∣ = ∣ O C → ∣ |\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}| ∣OA∣=∣OB∣=∣OC∣,则 O O O 是 △ A B C \triangle ABC △ABC的外心;
3、已知 O O O 为 △ A B C \triangle ABC △ABC内的一点,满足 O A → ⋅ O B → = O B → ⋅ O C → = O C → ⋅ O A → \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OB}\cdot\overrightarrow{OC}=\overrightarrow{OC}\cdot\overrightarrow{OA} OA⋅OB=OB⋅OC=OC⋅OA,则 O O O 是 △ A B C \triangle ABC △ABC的垂心;
4、已知 O O O 为 △ A B C \triangle ABC △ABC内的一点,的充要条件是 满足 O A → ⋅ ( A B → ∣ A B → ∣ − A C → ∣ A C → ∣ ) \overrightarrow{OA}\cdot(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}) OA⋅(∣AB∣AB−∣AC∣AC) = O B → ⋅ ( B A → ∣ B A → ∣ − B C → ∣ B C → ∣ ) = \overrightarrow{OB}\cdot(\cfrac{\overrightarrow{BA}}{|\overrightarrow{BA}|}-\cfrac{\overrightarrow{BC}}{|\overrightarrow{BC}|}) =OB⋅(∣BA∣BA−∣BC∣BC) = O C → ⋅ ( C A → ∣ C A → ∣ − C B → ∣ C B → ∣ ) = 0 =\overrightarrow{OC}\cdot(\cfrac{\overrightarrow{CA}}{|\overrightarrow{CA}|}-\cfrac{\overrightarrow{CB}}{|\overrightarrow{CB}|})=0 =OC⋅(∣CA∣CA−∣CB∣CB)=0,则 O O O 为 △ A B C \triangle ABC △ABC的内心 ;
三角形重心
- 重心:三角形的三条中线的交点。
✍️ 命题一:已知 O O O为 △ A B C \triangle ABC △ABC 内的一点,则 O O O是 △ A B C \triangle ABC △ABC的重心的充要条件是 O A → \overrightarrow{OA} OA + + + O B → \overrightarrow{OB} OB + + + O C → \overrightarrow{OC} OC = = = 0 ⃗ \vec{0} 0;
证明:必要性,由于 O O O是 △ A B C \triangle ABC △ABC的重心,则线段 A D 、 B E 、 C F AD、BE、CF AD、BE、CF为三角形的三条中线,
则有 A B → + A C → = 2 A D → = 4 3 A O → = − 4 3 O A → \overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}=\cfrac{4}{3}\overrightarrow{AO}=-\cfrac{4}{3}\overrightarrow{OA} AB+AC=2AD=34AO=−34OA,

B A → + B C → = 2 B E → = 4 3 B O → = − 4 3 O B → \overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BE}=\cfrac{4}{3}\overrightarrow{BO}=-\cfrac{4}{3}\overrightarrow{OB} BA+BC=2BE=34BO=−34OB,
C B → + C A → = 2 C F → = 4 3 C O → = − 4 3 O C → \overrightarrow{CB}+\overrightarrow{CA}=2\overrightarrow{CF}=\cfrac{4}{3}\overrightarrow{CO}=-\cfrac{4}{3}\overrightarrow{OC} CB+CA=2CF=34CO=−34OC,
故 O A → + O B → + O C → \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} OA+OB+OC = − 4 3 ( O A → + O B → + O C → ) =-\cfrac{4}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}) =−34(OA+OB+OC)
= A B → + A C → + B A → + B C → + C B → + C A → = 0 ⃗ =\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CB}+\overrightarrow{CA}=\vec{0} =AB+AC+BA+BC+CB+CA=0;
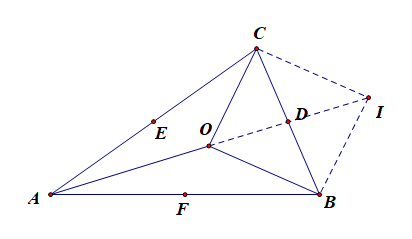
充分性,由 O A → + O B → + O C → = 0 ⃗ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0} OA+OB+OC=0,得到 O B → + O C → = − O A → \overrightarrow{OB}+\overrightarrow{OC}=-\overrightarrow{OA} OB+OC=−OA,
又 O B → + O C → = 2 O D → \overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OD} OB+OC=2OD,则 − O A → = 2 O D → -\overrightarrow{OA}=2\overrightarrow{OD} −OA=2OD,
故点 A 、 O 、 D A、O、D A、O、D三点共线,且 A D AD AD为三角形的一条中线;
同理, B E 、 C F BE、CF BE、CF为三角形的中线;故 O O O是 △ A B C \triangle ABC △ABC的重心;证毕。
这条性质在具体题目中又是如何使用的呢?应用举例分析:将给定条件先变形得到,$\overrightarrow{PB}$$+$$\overrightarrow{PC}$$-$$\overrightarrow{AP}$$=$$\vec{0}$,变形后即$\overrightarrow{PB}$$+$$\overrightarrow{PC}$$+$$\overrightarrow{PA}$$=$$\vec{0}$,故点$P$是三角形的重心。
✍️ 命题二: O O O是 △ A B C \triangle ABC △ABC的重心,则 S Δ A O B = S Δ B O C = S Δ C O A S_{\Delta AOB}=S_{\Delta BOC}=S_{\Delta COA} SΔAOB=SΔBOC=SΔCOA;
证明: O O O是 △ A B C \triangle ABC △ABC的重心,令边 A B AB AB上的高线为 h h h,
则 S Δ A O B = 1 2 ⋅ A B ⋅ h 3 = 1 3 S Δ A B C S_{\Delta AOB}=\cfrac{1}{2}\cdot AB\cdot \cfrac{h}{3}=\cfrac{1}{3}S_{\Delta ABC} SΔAOB=21⋅AB⋅3h=31SΔABC,
同理, S Δ B O C = 1 3 S Δ A B C S_{\Delta BOC}=\cfrac{1}{3}S_{\Delta ABC} SΔBOC=31SΔABC, S Δ A O C = 1 3 S Δ A B C S_{\Delta AOC}=\cfrac{1}{3}S_{\Delta ABC} SΔAOC=31SΔABC,
故 S Δ A O B = S Δ B O C = S Δ C O A S_{\Delta AOB}=S_{\Delta BOC}=S_{\Delta COA} SΔAOB=SΔBOC=SΔCOA;
✍️ 命题三:已知 D 、 E 、 F D、E、F D、E、F是 △ A B C \triangle ABC △ABC的边 B C 、 A C 、 A B BC、AC、AB BC、AC、AB的中点,则 A D → + B E → + C F → = 0 ⃗ \overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\vec{0} AD+BE+CF=0;
证明:已知 D 、 E 、 F D、E、F D、E、F是 △ A B C \triangle ABC △ABC的边 B C 、 A C 、 A B BC、AC、AB BC、AC、AB的中点, O O O是 △ A B C \triangle ABC △ABC的重心,
则 A D → = 1 2 ( A B → + A C → ) \overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC}) AD=21(AB+AC), B E → = 1 2 ( B C → + B A → ) \overrightarrow{BE}=\cfrac{1}{2}(\overrightarrow{BC}+\overrightarrow{BA}) BE=21(BC+BA), C F → = 1 2 ( C A → + C B → ) \overrightarrow{CF}=\cfrac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB}) CF=21(CA+CB),
故 A D → + B E → + C F → \overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF} AD+BE+CF = 1 2 ( A B → + A C → + B C → + B A → + C A → + C B → ) = 0 ⃗ =\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{CA}+\overrightarrow{CB}) =\vec{0} =21(AB+AC+BC+BA+CA+CB)=0;
三角形外心
- 外心:三角形的三条边的中垂线交点,也是外接圆的圆心;
✍️ 已知 O O O为 △ A B C \triangle ABC △ABC内的一点,满足 ∣ O A → ∣ = ∣ O B → ∣ = ∣ O C → ∣ |\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}| ∣OA∣=∣OB∣=∣OC∣,则 O O O 是 △ A B C \triangle ABC △ABC的外心;
证明:到三角形的三个顶点等距离的点是三角形的外接圆的圆心,故 O O O 是 △ A B C \triangle ABC △ABC的外心;
三角形垂心
- 垂心:三角形的三条边的高线的交点。
✍️ 命题一:已知 O O O为 △ A B C \triangle ABC △ABC内的一点,满足 O A → ⋅ O B → = O B → ⋅ O C → = O C → ⋅ O A → \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OB}\cdot\overrightarrow{OC}=\overrightarrow{OC}\cdot\overrightarrow{OA} OA⋅OB=OB⋅OC=OC⋅OA,则 O O O是 △ A B C \triangle ABC △ABC的垂心;
证明:由于 O A → ⋅ O B → = O C → ⋅ O A → \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OA} OA⋅OB=OC⋅OA,则 O A → ⋅ ( O B → − O C → ) = 0 \overrightarrow{OA}\cdot(\overrightarrow{OB}-\overrightarrow{OC})=0 OA⋅(OB−OC)=0,
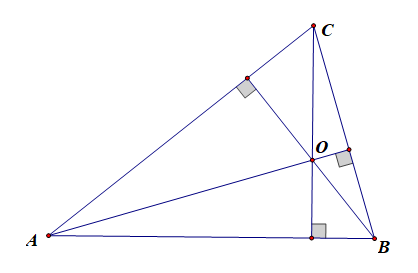
即 O A → ⋅ C B → = 0 \overrightarrow{OA}\cdot\overrightarrow{CB}=0 OA⋅CB=0,则 O A ⊥ B C OA\perp BC OA⊥BC,
同理 O A → ⋅ O B → = O B → ⋅ O C → \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OB}\cdot\overrightarrow{OC} OA⋅OB=OB⋅OC,可得 O B ⊥ A C OB\perp AC OB⊥AC,
O B → ⋅ O C → = O C → ⋅ O A → \overrightarrow{OB}\cdot\overrightarrow{OC}=\overrightarrow{OC}\cdot\overrightarrow{OA} OB⋅OC=OC⋅OA,可得 O C ⊥ A B OC\perp AB OC⊥AB,
故 O O O是 △ A B C \triangle ABC △ABC的垂心;
✍️ 命题二:已知 O O O为 △ A B C \triangle ABC △ABC所在平面内的一点,且 ∣ O A → ∣ 2 |\overrightarrow{OA}|^2 ∣OA∣2 + + + ∣ B C → ∣ 2 |\overrightarrow{BC}|^2 ∣BC∣2 = ∣ O B → ∣ 2 + =|\overrightarrow{OB}|^2+ =∣OB∣2+ ∣ C A → ∣ 2 |\overrightarrow{CA}|^2 ∣CA∣2 = ∣ O C → ∣ 2 + =|\overrightarrow{OC}|^2+ =∣OC∣2+ ∣ A B → ∣ 2 |\overrightarrow{AB}|^2 ∣AB∣2,则 O O O是 △ A B C \triangle ABC △ABC的垂心;
三角形内心
- 内心:三角形的三个内角平分线的交点,也是内切圆的圆心;
✍️ 命题一: O O O为 △ A B C \triangle ABC △ABC的内心的充要条件是 O A → ⋅ ( A B → ∣ A B → ∣ − A C → ∣ A C → ∣ ) \overrightarrow{OA}\cdot(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}) OA⋅(∣AB∣AB−∣AC∣AC) = O B → ⋅ ( B A → ∣ B A → ∣ − B C → ∣ B C → ∣ ) = \overrightarrow{OB}\cdot(\cfrac{\overrightarrow{BA}}{|\overrightarrow{BA}|}-\cfrac{\overrightarrow{BC}}{|\overrightarrow{BC}|}) =OB⋅(∣BA∣BA−∣BC∣BC) = O C → ⋅ ( C A → ∣ C A → ∣ − C B → ∣ C B → ∣ ) = 0 =\overrightarrow{OC}\cdot(\cfrac{\overrightarrow{CA}}{|\overrightarrow{CA}|}-\cfrac{\overrightarrow{CB}}{|\overrightarrow{CB}|})=0 =OC⋅(∣CA∣CA−∣CB∣CB)=0
证明:充分性,如图,向量 A B → \overrightarrow{AB} AB、 A C → \overrightarrow{AC} AC的单位向量分别是 A E → \overrightarrow{AE} AE、 A D → \overrightarrow{AD} AD,
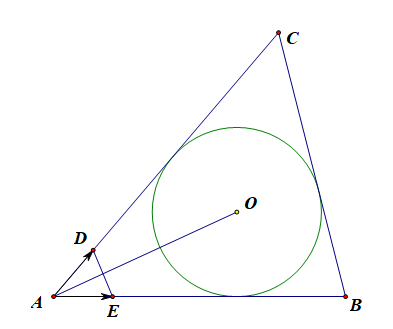
则 Δ A D E \Delta ADE ΔADE为等腰三角形,
由 O A → ⋅ ( A B → ∣ A B → ∣ − A C → ∣ A C → ∣ ) \overrightarrow{OA}\cdot (\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}) OA⋅(∣AB∣AB−∣AC∣AC) = O A → ⋅ ( A E → − A D → ) =\overrightarrow{OA}\cdot (\overrightarrow{AE}-\overrightarrow{AD}) =OA⋅(AE−AD) = O A → ⋅ D E → = 0 =\overrightarrow{OA}\cdot \overrightarrow{DE}=0 =OA⋅DE=0,
故 O A OA OA为 ∠ A \angle A ∠A的平分线;同理可得 O B OB OB、 O C OC OC分别为 ∠ B 、 ∠ C \angle B、\angle C ∠B、∠C的平分线;
故点 O O O是 △ A B C \triangle ABC △ABC的内心。
必要性,由点 O O O是 △ A B C \triangle ABC △ABC的内心,则可知 O A OA OA为 ∠ A \angle A ∠A的平分线,
故容易知道 O A → ⋅ D E → = 0 \overrightarrow{OA}\cdot \overrightarrow{DE}=0 OA⋅DE=0,
即 O A → ⋅ ( A B → ∣ A B → ∣ − A C → ∣ A C → ∣ ) = 0 \overrightarrow{OA}\cdot(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})=0 OA⋅(∣AB∣AB−∣AC∣AC)=0,
同理可知$ \overrightarrow{OB}\cdot(\cfrac{\overrightarrow{BA}}{|\overrightarrow{BA}|}-\cfrac{\overrightarrow{BC}}{|\overrightarrow{BC}|})$ = O C → ⋅ ( C A → ∣ C A → ∣ − C B → ∣ C B → ∣ ) = 0 =\overrightarrow{OC}\cdot(\cfrac{\overrightarrow{CA}}{|\overrightarrow{CA}|}-\cfrac{\overrightarrow{CB}}{|\overrightarrow{CB}|})=0 =OC⋅(∣CA∣CA−∣CB∣CB)=0,证毕。
典例剖析
【人教 2019 A 2019A 2019A 版教材 P 52 P_{52} P52 页习题 6.4 6.4 6.4 第 2 2 2 题】已知 O O O, N N N, P P P 在 △ A B C \triangle ABC △ABC 所在平面内,满足 ∣ O A → ∣ |\overrightarrow{OA}| ∣OA∣ = = = ∣ O B → ∣ |\overrightarrow{OB}| ∣OB∣ = = = ∣ O C → ∣ |\overrightarrow{OC}| ∣OC∣, N A → \overrightarrow{NA} NA + + + N B → \overrightarrow{NB} NB + + + N C → \overrightarrow{NC} NC = = = 0 ⃗ \vec{0} 0, 且 P A → \overrightarrow{PA} PA ⋅ \cdot ⋅ P B → \overrightarrow{PB} PB = = = P B → \overrightarrow{PB} PB ⋅ \cdot ⋅ P C → \overrightarrow{PC} PC = = = P C → \overrightarrow{PC} PC ⋅ \cdot ⋅ P A → \overrightarrow{PA} PA, 则点 O O O, N N N, P P P 依次是 △ A B C \triangle ABC △ABC 的 【 \qquad 】
解:若 ∣ O A → ∣ |\overrightarrow{OA}| ∣OA∣ = = = ∣ O B → ∣ |\overrightarrow{OB}| ∣OB∣ = = = ∣ O C → ∣ |\overrightarrow{OC}| ∣OC∣,则 O O O 为 △ A B C \triangle ABC △ABC 的外心; 若 N A → \overrightarrow{NA} NA + + + N B → \overrightarrow{NB} NB + + + N C → \overrightarrow{NC} NC = = = 0 ⃗ \vec{0} 0, 则 N N N 为 △ A B C \triangle ABC △ABC 的重心; 若 P A → \overrightarrow{PA} PA ⋅ \cdot ⋅ P B → \overrightarrow{PB} PB = = = P B → \overrightarrow{PB} PB ⋅ \cdot ⋅ P C → \overrightarrow{PC} PC = = = P C → \overrightarrow{PC} PC ⋅ \cdot ⋅ P A → \overrightarrow{PA} PA, 则 P P P 为 △ A B C \triangle ABC △ABC 的垂心,故选 C C C .
【网络上看到的题目】 已知 O O O 是平面上的一定点, A A A、 B B B、 C C C 是平面上不共线的三个点, 动点 P P P 满足以下的表达式: O P → \overrightarrow{OP} OP = = = O B → + O C → 2 \cfrac{\overrightarrow{OB}+\overrightarrow{OC}}{2} 2OB+OC + + + λ \lambda λ ( A B → ∣ A B → ∣ cos B \Big(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B} (∣AB∣cosBAB + + + A C → ∣ A C → ∣ cos C ) \cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}\Big) ∣AC∣cosCAC), λ ∈ [ 0 , + ∞ ) \lambda\in[0,+\infty) λ∈[0,+∞), 则动点 P P P 的轨迹一定通过 △ A B C \triangle ABC △ABC 的【 \qquad 】
解: 设 B C BC BC 的中点为 D D D,
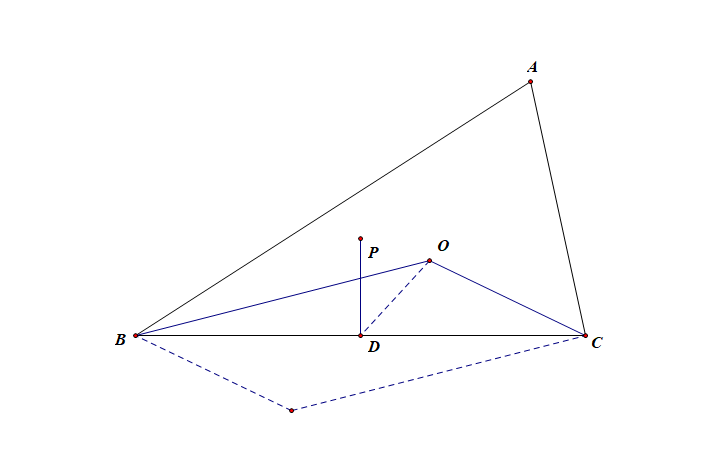
O P → = O B → + O C → 2 + λ ( A B → ∣ A B → ∣ cos B + A C → ∣ A C → ∣ cos C ) = O D → + λ ( A B → ∣ A B → ∣ cos B + A C → ∣ A C → ∣ cos C ) \overrightarrow{OP}=\cfrac{\overrightarrow{OB}+\overrightarrow{OC}}{2}+\lambda\Big(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}| \cos B}+\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}\Big)=\overrightarrow{OD}+\lambda\Big(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B}+\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}\Big) OP=2OB+OC+λ(∣AB∣cosBAB+∣AC∣cosCAC)=OD+λ(∣AB∣cosBAB+∣AC∣cosCAC)
即 D P → = λ ( A B → ∣ A B → ∣ cos B + A C → ∣ A C → ∣ cos C ) \overrightarrow{DP}=\lambda\Big(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B}+\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}\Big) DP=λ(∣AB∣cosBAB+∣AC∣cosCAC)
两端同时点乘向量 B C → \overrightarrow{BC} BC,得到
D P → ⋅ B C → \overrightarrow{DP}\cdot\overrightarrow{BC} DP⋅BC = = = λ ( A B → ⋅ B C → ∣ A B → ∣ cos B + A C → ⋅ B C → ∣ A C → ∣ cos C ) \lambda\Big(\cfrac{\overrightarrow{AB}\cdot\overrightarrow{BC}}{|\overrightarrow{AB}|\cos B}+\cfrac{\overrightarrow{AC}\cdot\overrightarrow{BC}}{|\overrightarrow{AC}|\cos C}\Big) λ(∣AB∣cosBAB⋅BC+∣AC∣cosCAC⋅BC)
= = = λ ( ∣ A B → ∣ ⋅ ∣ B C → ∣ cos ( π − B ) ∣ A B → ∣ cos B + ∣ A C → ∣ ⋅ ∣ B C → ∣ cos C ∣ A C → ∣ cos C ) \lambda\Big(\cfrac{|\overrightarrow{AB}|\cdot|\overrightarrow{BC}|\cos(\pi-B)}{|\overrightarrow{AB}|\cos B}+\cfrac{|\overrightarrow{AC}|\cdot|\overrightarrow{BC}|\cos C}{|\overrightarrow{AC}|\cos C}\Big) λ(∣AB∣cosB∣AB∣⋅∣BC∣cos(π−B)+∣AC∣cosC∣AC∣⋅∣BC∣cosC)
= = = λ ( − ∣ B C → ∣ + ∣ B C → ∣ ) = 0 \lambda(-|\overrightarrow{BC}|+|\overrightarrow{BC}|)=0 λ(−∣BC∣+∣BC∣)=0
所以 D P ⊥ B C DP\perp BC DP⊥BC,点 P P P 在 B C BC BC 的垂直平分线上, 即 P P P 经过 △ A B C \triangle ABC △ABC 的外心,故选 D D D .
【2024高一联考题】“奔驰定理” 因其对应的几何图形酷似某汽车品牌标志而得名,它是平面向量中一个非常优美的结论 . 该定理与三角形四心(重心、内心、外心、垂心)有着神秘的关联,定理的具体视频讲解内容是: 如图,已知 M M M 是 △ A B C \triangle ABC △ABC 内一点, △ B M C \triangle BMC △BMC, △ A M C \triangle AMC △AMC, △ A M B \triangle AMB △AMB 的面积分别为 S A S_A SA, S B S_B SB, S C S_C SC, 则有 S A ⋅ M A → S_A\cdot\overrightarrow{MA} SA⋅MA + + + S B ⋅ M B → S_B\cdot \overrightarrow{MB} SB⋅MB + + + S C ⋅ M C → S_C\cdot \overrightarrow{MC} SC⋅MC = = = 0 ⃗ \vec{0} 0 成立 . 根据题意, 以下命题中正确的有 【 \qquad 】
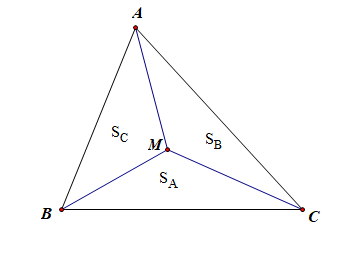
解析: 对于选项 A A A 而言,如图,由 S A ⋅ M A → S_A\cdot\overrightarrow{MA} SA⋅MA + + + S B ⋅ M B → S_B\cdot \overrightarrow{MB} SB⋅MB + + + S C ⋅ M C → S_C\cdot \overrightarrow{MC} SC⋅MC = = = 0 ⃗ \vec{0} 0 ,且 S A : S B : S C S_A:S_B:S_C SA:SB:SC= 1 : 1 : 1 1:1:1 1:1:1,令 S A = S B = S C = k S_A=S_B=S_C=k SA=SB=SC=k,代入已知条件,约分得到,
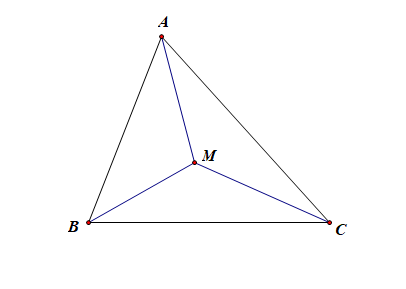
则 M A → \overrightarrow{MA} MA + + + M B → \overrightarrow{MB} MB + + + M C → \overrightarrow{MC} MC = = = 0 ⃗ \vec{0} 0 ,则 M M M 为三角形的重心。故 A A A 正确;
对于选项 B B B 而言,由于点 M M M 为 △ \triangle △ A B C ABC ABC的内心, 是三角形的三条角平分线的交点,如图,
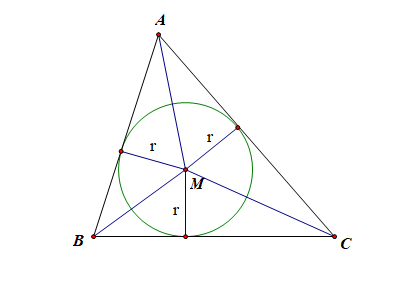
由 S A ⋅ M A → S_A\cdot\overrightarrow{MA} SA⋅MA + + + S B ⋅ M B → S_B\cdot \overrightarrow{MB} SB⋅MB + + + S C ⋅ M C → S_C\cdot \overrightarrow{MC} SC⋅MC = = = 0 ⃗ \vec{0} 0 ,
又 S A = 1 2 B C × r S_A=\cfrac{1}{2}BC\times r SA=21BC×r, S B = 1 2 A C × r S_B=\cfrac{1}{2}AC\times r SB=21AC×r, S C = 1 2 A B × r S_C=\cfrac{1}{2}AB\times r SC=21AB×r,
即 1 2 B C × r × ⋅ M A → \cfrac{1}{2}BC\times r\times\cdot\overrightarrow{MA} 21BC×r×⋅MA + + + 1 2 A C × r × ⋅ M B → \cfrac{1}{2}AC\times r\times\cdot \overrightarrow{MB} 21AC×r×⋅MB + + + 1 2 A B × r × ⋅ M C → \cfrac{1}{2}AB\times r\times\cdot \overrightarrow{MC} 21AB×r×⋅MC = = = 0 ⃗ \vec{0} 0 ,约分整理得到,
B C BC BC ⋅ \cdot ⋅ M A → \overrightarrow{MA} MA + + + A C AC AC ⋅ \cdot ⋅ M B → \overrightarrow{MB} MB + + + A B AB AB ⋅ \cdot ⋅ M C → \overrightarrow{MC} MC = = = O ⃗ \vec{O} O,故 B B B 正确;
对于选项 C C C 而言,由于点 M M M 为 △ \triangle △ A B C ABC ABC的外心,则点 M M M 为三条边的中垂线的交点,且 M A MA MA = = = M B MB MB = = = M C MC MC = = = R R R,如图由 ∠ 1 \angle1 ∠1 + + + ∠ 2 \angle2 ∠2 = = = 7 5 ∘ 75^{\circ} 75∘, ∠ 2 \angle2 ∠2 + + + ∠ 3 \angle3 ∠3 = = = 4 5 ∘ 45^{\circ} 45∘, ∠ 1 \angle1 ∠1 + + + ∠ 3 \angle3 ∠3 = = = 6 0 ∘ 60^{\circ} 60∘,可以求得 ∠ 1 \angle1 ∠1 = = = 4 5 ∘ 45^{\circ} 45∘, ∠ 2 \angle2 ∠2 = = = 3 0 ∘ 30^{\circ} 30∘, ∠ 3 \angle3 ∠3 = = = 1 5 ∘ 15^{\circ} 15∘,故 ∠ \angle ∠ B M C BMC BMC = = = 9 0 ∘ 90^{\circ} 90∘, ∠ \angle ∠ C M A CMA CMA = = = 12 0 ∘ 120^{\circ} 120∘, ∠ \angle ∠ A M B AMB AMB = = = 15 0 ∘ 150^{\circ} 150∘,
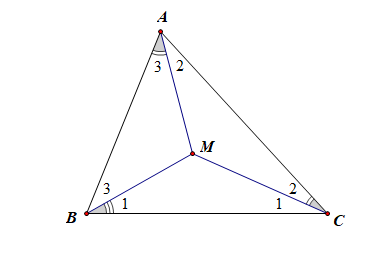
则由三角形面积公式可知, S A = 1 2 × R 2 × sin 9 0 ∘ S_{A}=\cfrac{1}{2}\times R^2\times\sin 90^{\circ} SA=21×R2×sin90∘,
S B = 1 2 × R 2 × sin 12 0 ∘ S_{B}=\cfrac{1}{2}\times R^2\times\sin 120^{\circ} SB=21×R2×sin120∘, S C = 1 2 × R 2 × sin 15 0 ∘ S_{C}=\cfrac{1}{2}\times R^2\times\sin 150^{\circ} SC=21×R2×sin150∘,
故 S A : S B : S C = sin 9 0 ∘ : sin 12 0 ∘ : sin 15 0 ∘ = 1 : 3 2 : 1 2 = 2 : 3 : 1 S_{A}:S_{B}:S_{C}=\sin 90^{\circ}:\sin 120^{\circ}:\sin 150^{\circ}=1:\cfrac{\sqrt{3}}{2}:\cfrac{1}{2}=2:\sqrt{3}:1 SA:SB:SC=sin90∘:sin120∘:sin150∘=1:23:21=2:3:1,故 C C C 错误;
对于选项 D D D 而言,由于点 M M M 为 △ \triangle △ A B C ABC ABC的垂心,是三角形的三条高线的交点,如图,
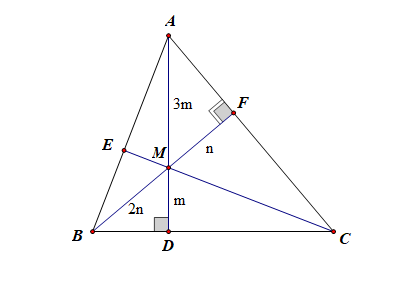
由题目 S A ⋅ M A → S_A\cdot\overrightarrow{MA} SA⋅MA + + + S B ⋅ M B → S_B\cdot \overrightarrow{MB} SB⋅MB + + + S C ⋅ M C → S_C\cdot\overrightarrow{MC} SC⋅MC = = = 0 ⃗ \vec{0} 0 ,又 3 M A → 3\overrightarrow{MA} 3MA + + + 4 M B → 4\overrightarrow{MB} 4MB + + + 5 M C → 5\overrightarrow{MC} 5MC = = = 0 ⃗ \vec{0} 0,则可知 S A : S B : S C S_A:S_B:S_C SA:SB:SC= 3 : 4 : 5 3:4:5 3:4:5,故 S A S A + S B + S C \cfrac{S_{A}}{S_A+S_B+S_C} SA+SB+SCSA = = = 3 3 + 4 + 5 \cfrac{3}{3+4+5} 3+4+53 = = = 1 4 \cfrac{1}{4} 41,故 M D A D \cfrac{MD}{AD} ADMD = = = 1 4 \cfrac{1}{4} 41,同理可得, M F B F \cfrac{MF}{BF} BFMF = = = 1 3 \cfrac{1}{3} 31,故可设, M D = m MD=m MD=m, A M = 3 m AM=3m AM=3m, M F = n MF=n MF=n, B M = 2 n BM=2n BM=2n,
在 R t △ B M D Rt\triangle BMD Rt△BMD 中,由 cos ∠ B M D = m 2 n = cos ∠ A M F = n 3 m \cos\angle BMD=\cfrac{m}{2n}=\cos\angle AMF=\cfrac{n}{3m} cos∠BMD=2nm=cos∠AMF=3mn,故得到 3 m 2 = 2 n 2 3m^2=2n^2 3m2=2n2,即 n = 6 2 m n=\cfrac{\sqrt{6}}{2}m n=26m,
则 cos ∠ B M D = m 2 n = 6 6 \cos\angle BMD=\cfrac{m}{2n}=\cfrac{\sqrt{6}}{6} cos∠BMD=2nm=66,故 cos ∠ A M B = cos ( π − ∠ B M D ) = − 6 6 \cos\angle AMB=\cos(\pi-\angle BMD)=-\cfrac{\sqrt{6}}{6} cos∠AMB=cos(π−∠BMD)=−66 . 故 D D D 正确;
综上所述,选 A B D ABD ABD;
【人教 2019A 版教材 P 152 P_{152} P152 页练习第4题】过 △ A B C \triangle ABC △ABC 所在平面 α \alpha α 外一点 P P P,作 P O ⊥ α PO\perp\alpha PO⊥α,垂足为 O O O, 连接 P A PA PA, P B PB PB, P C PC PC .
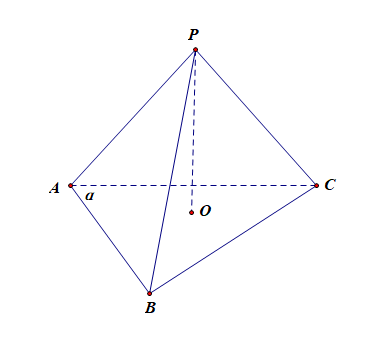
(1). 若 P A = P B = P C PA=PB=PC PA=PB=PC,则点 O O O 是 △ A B C \triangle ABC △ABC 的( 外 )心.
法1:连结 A O AO AO、 B O BO BO、 C O CO CO,由已知可得, ∠ P O A = ∠ P O B = ∠ P O C \angle POA=\angle POB=\angle POC ∠POA=∠POB=∠POC,
由于 P A = P B = P C PA=PB=PC PA=PB=PC 且 P O PO PO 公用, 由勾股定理可知, O A = O B = O C OA=OB=OC OA=OB=OC,故点 O O O 是 △ A B C \triangle ABC △ABC 的外心 .
法2:动态思维,让点 P P P 沿着线段 P O PO PO 运动,并保持线面垂直关系不变,最后点 P P P 和点 O O O 重合,即关系 P A PA PA = = = P B PB PB = = = P C PC PC 变为 O A OA OA = = = O B OB OB = = = O C OC OC,故点 O O O 是 △ A B C \triangle ABC △ABC 的外心 .
(2). 若 P A = P B = P C PA=PB=PC PA=PB=PC, ∠ C = 9 0 ∘ \angle C=90^{\circ} ∠C=90∘, 则点 O O O 是 A B AB AB 边的( 中 )点 .
解析:由 (1) 可知,由条件 P A = P B = P C PA=PB=PC PA=PB=PC 可以推知点 O O O 是 △ A B C \triangle ABC △ABC 的外心,再加上 条件 ∠ C = 9 0 ∘ \angle C=90^{\circ} ∠C=90∘,故此时外心就在直角三角形的斜边 A B AB AB 的中点处,故点 O O O 是 A B AB AB 边的中点 .
(3). 若 P A ⊥ P B PA\perp PB PA⊥PB, P B ⊥ P C PB\perp PC PB⊥PC, P C ⊥ P A PC \perp PA PC⊥PA, 垂足都为 P P P, 则点 O O O 是 △ A B C \triangle ABC △ABC 的( 垂 )心.

解析:连结 C O CO CO 并延长交 A B AB AB 于点 D D D,连结 A O AO AO 并延长交 B C BC BC 于点 E E E,
由于 P C ⊥ P A PC\perp PA PC⊥PA, P C ⊥ P B PC\perp PB PC⊥PB, P A ⊂ PA\subset PA⊂ 平面 P A B PAB PAB, P B ⊂ PB\subset PB⊂ 平面 P A B PAB PAB, P A ∩ P B = P PA\cap PB=P PA∩PB=P,
则可得 P C ⊥ PC\perp PC⊥ 平面 P A B PAB PAB,
又由于 A B ⊂ AB\subset AB⊂ 平面 P A B PAB PAB,则 P C ⊥ A B PC\perp AB PC⊥AB,即 A B ⊥ P C AB\perp PC AB⊥PC,
又由于 P O ⊥ PO\perp PO⊥ 平面 A B C ABC ABC,且 A B ⊂ AB\subset AB⊂ 平面 A B C ABC ABC,则 P O ⊥ A B PO\perp AB PO⊥AB,即 A B ⊥ P O AB\perp PO AB⊥PO,
即 A B ⊥ P C AB\perp PC AB⊥PC, A B ⊥ P O AB\perp PO AB⊥PO, P O ⊂ PO\subset PO⊂ 平面 P C D PCD PCD, P C ⊂ PC\subset PC⊂ 平面 P C D PCD PCD, P C ∩ P O = P PC\cap PO=P PC∩PO=P,
则可得 A B ⊥ C D AB\perp CD AB⊥CD,即 C D ⊥ A B CD\perp AB CD⊥AB,故 C D CD CD 为三角形的高线,
同理可证, A E ⊥ B C AE\perp BC AE⊥BC,故 A E AE AE 为三角形的高线,
即此时点 O O O 是三角形的高线的交点,故点 O O O 是 △ A B C \triangle ABC △ABC 的垂心.
解题经验
在具体的题目求解中,关于多个向量的线性表示形式,其难点往往是其系数的恰当拆分。
1、 若已知 A B → + A C → = 2 A E → \overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AE} AB+AC=2AE,或者 A E → = 1 2 ( A B → + A C → ) \overrightarrow{AE}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC}) AE=21(AB+AC),则可知点 E E E为 B C BC BC的中点;
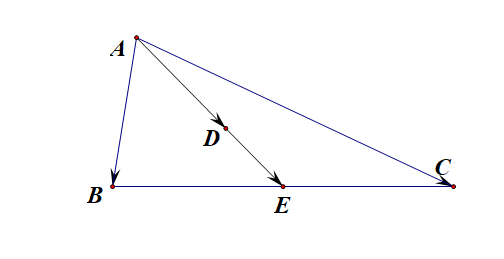
已知 A B → + A C → = 3 A D → \overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD} AB+AC=3AD,则 3 A D → = 2 A E → 3\overrightarrow{AD}=2\overrightarrow{AE} 3AD=2AE,则 A D → = 2 3 A E → \overrightarrow{AD}=\cfrac{2}{3}\overrightarrow{AE} AD=32AE,可知点 D D D为 △ A B C \triangle ABC △ABC的重心;
2、若由题目可知 O A → + 2 O B → + 3 O C → = 0 ⃗ \overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0} OA+2OB+3OC=0,将其系数做恰当的拆分得到, ( O A → (\overrightarrow{OA} (OA + + + O C → ) \overrightarrow{OC}) OC) + 2 ( O B → +2(\overrightarrow{OB} +2(OB + O C → ) +\overrightarrow{OC}) +OC) = = = 0 ⃗ \vec{0} 0,如图即 2 O D → 2\overrightarrow{OD} 2OD = = = − 4 O E → -4\overrightarrow{OE} −4OE,即 O D → \overrightarrow{OD} OD = = = − 2 O E → -2\overrightarrow{OE} −2OE,即可知点 O O O一定在 △ A B C \triangle ABC △ABC 的中位线 D E DE DE 上,且在中位线上靠近点 E E E 的三等分点处。
延申知识
已知 O O O 是 △ A B C \triangle ABC △ABC 所在平面上的一点, a a a, b b b, c c c 为 △ A B C \triangle ABC △ABC 的三边长,若 a a a ⋅ \cdot ⋅ O A → \overrightarrow{OA} OA + + + b b b ⋅ \cdot ⋅ O B → \overrightarrow{OB} OB + + + c c c ⋅ \cdot ⋅ O C → \overrightarrow{OC} OC = = = 0 0 0, 则 O O O 是 △ A B C \triangle ABC △ABC 的内心。
证明: O B → = O A → + A B → \overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB} OB=OA+AB , O C → = O A → + A C → \overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC} OC=OA+AC,
则 a ⋅ O A → a\cdot \overrightarrow{OA} a⋅OA + + + b ⋅ O B → b\cdot\overrightarrow{OB} b⋅OB + + + c ⋅ O C → c\cdot\overrightarrow{OC} c⋅OC = = = 0 0 0 ⇔ \Leftrightarrow ⇔ ( a + b + c ) ⋅ O A → (a+b+c)\cdot\overrightarrow{OA} (a+b+c)⋅OA + + + b ⋅ A B → b\cdot\overrightarrow{AB} b⋅AB + + + c ⋅ A C → = 0 c\cdot\overrightarrow{AC}=0 c⋅AC=0,
等式两边同时除以 b c bc bc 得, A O → = b c a + b + c ( A B → ∣ A B ∣ + A C → ∣ A C ∣ ) \overrightarrow{AO}=\cfrac{bc}{a+b+c}\left(\cfrac{\overrightarrow{AB}}{|AB|}+\cfrac{\overrightarrow{AC}}{|AC|}\right) AO=a+b+cbc ∣AB∣AB+∣AC∣AC ,则可知 A O AO AO 为 ∠ B A C \angle BAC ∠BAC 的角平分线,同理 B O BO BO 、 C O CO CO 分别为 ∠ A B C \angle ABC ∠ABC 、 ∠ A C B \angle ACB ∠ACB 的角平分线,所以 O O O 是 △ A B C \triangle ABC △ABC 的内心。
✍️ 命题四:平行四边形 A B C D ABCD ABCD的中心是 O O O, P P P为平面上任意一点,则 P O → = 1 4 ( P A → + P B → + P C → + P D → ) \overrightarrow{PO}=\cfrac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}) PO=41(PA+PB+PC+PD);
证明:平行四边形 A B C D ABCD ABCD的中心是 O O O, P P P为平面上任意一点,

则在 Δ P A C \Delta PAC ΔPAC中, P A → + P C → = 2 P O → \overrightarrow{PA}+\overrightarrow{PC}=2\overrightarrow{PO} PA+PC=2PO,在 Δ P B D \Delta PBD ΔPBD中, P B → + P D → = 2 P O → \overrightarrow{PB}+\overrightarrow{PD}=2\overrightarrow{PO} PB+PD=2PO,
故 P A → + P C → + P B → + P D → \overrightarrow{PA}+\overrightarrow{PC}+\overrightarrow{PB}+\overrightarrow{PD} PA+PC+PB+PD = 4 P O → =4\overrightarrow{PO} =4PO,
即 P O → = 1 4 ( P A → + P B → + P C → + P D → ) \overrightarrow{PO}=\cfrac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}) PO=41(PA+PB+PC+PD);
✍️ 已知 O O O为 △ A B C \triangle ABC △ABC的外心, H H H为其垂心,则 O H → = O A → + O B → + O C → \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} OH=OA+OB+OC.






















 1956
1956

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










