直线参数方程何时必须化为标准形式

前言

在求解直线与圆相交得到的弦的长度问题时，可以采用的思路很多：

①利用几何方法，即利用弦心距、半弦长、半径组成的$Rt△$来求解决；

②弦长公式，即$|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|$来求解；

③利用直线的参数方程的参数的几何意义来求解；

思路引申

当涉及到的是直线和圆时，此时思路①最简单快捷；但是从思路可移植的角度来思考[比如问题变化为直线和圆锥曲线相交得到的弦长问题]，思路③应该是最值得掌握的思路，此时思路①已经不能用了，思路②的运算量往往比较大，容易出错；

但思路③有个问题，在使用直线的参数方程时，必须要检验其是参数方程的标准形式，否则结果往往会出错；在此有两个问题：其一，为什么使用直线的参数方程的几何意义求弦长问题简单？其二，为什么必须将直线的参数方程的非标准形式转化为标准形式？

问题解析

预备知识：

• 借助一维数轴来理解$t$的几何意义

我们知道，一维数轴上的点和实数是一一对应的，如图所示，水平放置的数轴，其上的点$A$、$O$、$B$、$C$、$D$分别代表实数$-2$，$0$，$1$，$2$，$3$；动点对应的实数标记为$t$，那么$t=2$就对应点$C$，$t=-2$就对应点$A$，$t=0$就对应点$O$，$t=1$就对应点$B$，当变量$t$取遍所有的实数，那么动点就能代表数轴上所有的实数。这时候实数$t$就是数轴上的动点的一维坐标。

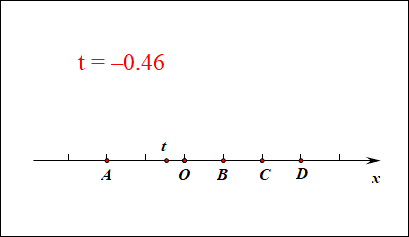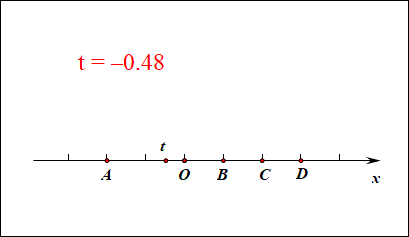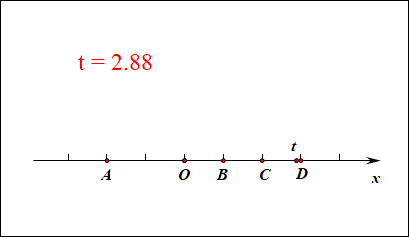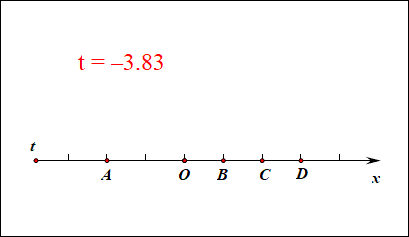
作用：此时若求线段的长度，则线段$AB=|t_A-t_B|=|-2-1|=3$;线段$BD=$$|t_B-t_D|$$=|1-3|$$=2$;

接下来，我们利用如下的参数方程[已经是标准形式]来求线段长或弦长；

在平面直角坐标系$xOy$中，直线$l$的参数方程为$\{\begin{array}{l}x=2+\frac{\sqrt{2}}{2}t\\ y=1+\frac{\sqrt{2}}{2}t\end{array}$($t$为参数)，

问题1：为什么使用直线的参数方程的几何意义求弦长问题简单？

当$t_0=0$时，其对于点$P_0(2，1)$；当$t_1=1$时，其对于点$P_1(2+\frac{\sqrt{2}}{2}，1+\frac{\sqrt{2}}{2})$；

此时求线段$|P_0{P}_1|$的长度，可以用如下的两个思路来求解：

思路①：$|P_0{P}_1|=\sqrt{(2+\frac{\sqrt{2}}{2}-2{)}^2+(1+\frac{\sqrt{2}}{2}-1{)}^2}=\sqrt{(\frac{\sqrt{2}}{2}{)}^2+(\frac{\sqrt{2}}{2}{)}^2}=1$；

思路②：$|P_0{P}_1|=|t_0-t_1|=|0-1|=1$；

很显然，思路②的运算简单的多，只是好些同学不懂得为什么要这样计算？

很显然，思路 ① 采用的是两个点的二维坐标来运算，而思路 ② 是利用两个点的一维坐标来计算，如上图所示，点$P_0$类似于数轴中的原点，那么点$P_1$是数轴右方的第一个单位点，点$P_2$是数轴右方的第二个单位点，故$|P_0{P}_1|$的长应该是一个单位。故利用一维坐标肯定比二维坐标计算量要小。

问题2：为什么必须将直线的参数方程的非标准形式转化为标准形式？

预备知识：在平面直角坐标系$xoy$中，直线$l$的参数方程为$\{\begin{array}{l}x=2+t\\ y=1+2t\end{array}$($t$为参数)，

如上图所示，当$t_0=0$时，对应上图中的点$A(2,1)$，当$t_1=1$时，对应上图中的点$B(3,3)$，

此时$|AB|=\sqrt{(2-3{)}^2+(1-3{)}^2}=\sqrt{5}$；其长度不是一个单位长，故其不是参数方程的标准形式，

在教学实践中，我们常用参数$t$前面的两个系数的平方和是否等于$1$来判断是否为标准形式；

如上，$1^2+2^2=5\ne 1$，故上述的参数方程不是标准形式。

如果直线的参数方程不是标准形式，则其参数$t$的几何意义就不是动点到定点的有向线段的数量，类似于我们不用标准的米尺测量人的身高，则测量的身高数据一定是不准确的；故使用前必须保证其为标准形式；

那么，如何将参数方程的非标准形式转化为标准形式呢，请参照下述例题中的具体解法来体会。

• 非标准形式化为标准形式的思路

$\{\begin{array}{l}x=x_0+at=x_0+\frac{a}{\sqrt{a^2+b^2}}\cdot \sqrt{a^2+b^2}t\\ y=y_0+bt=y_0+\frac{b}{\sqrt{a^2+b^2}}\cdot \sqrt{a^2+b^2}t\end{array}(t为参数)$，

再令$\sqrt{a^2+b^2}t=m$，则得到$\{\begin{array}{l}x=x_0+cos\theta m\\ y=y_0+sin\theta m\end{array}(m为参数)$，这才是标准形式；

此时的参数$m$的几何意义才是定点到动点的有向线段的数量。

举例，将非标准形式 $\{\begin{array}{l}x=-2-\sqrt{2}t\\ y=3+\sqrt{2}t\end{array}$ ($t$为参数)， 变形为直线的参数方程的标准形式 $\{\begin{array}{l}x=-2-\frac{\sqrt{2}}{2}(2t)\\ y=3+\frac{\sqrt{2}}{2}(2t)\end{array}$ ($2t$为参数)

案例分析

【北师大选修教材4-4 $P_{{}_{53}}$ $A$组第 $8$ 题】 求直线 $\{\begin{array}{l}x=-\frac{\sqrt{3}}{2}t\\ y=2+\frac{t}{2}\end{array},$ ( $t$ 为参数) 被曲线 $y^2-3x^2=0$ 截得的线段长.

解析：将直线的参数方程 $\{\begin{array}{l}x=-\frac{\sqrt{3}}{2}t\\ y=2+\frac{t}{2}\end{array}$ ($t$ 为参数)代人曲线方程 $y^2-3x^2=0$，

得 $t^2-t-2=0$，解得 $t_1=2$， $t_2=-1$，

由参数的儿何意义知，截得的线段长为 $|t_1-t_2|=|2-(-1)|=3$.

【2019届凤中高三理科月考1第22题】在平面直角坐标系$xoy$中，直线$l$的参数方程为$\{\begin{array}{l}x=2+t\\ y=1+2t\end{array}$($t$为参数)，以原点为极点，以$x$轴的非负半轴为极轴建立极坐标系，$\odot C$的极坐标方程为${\rho }^2$$-4\rho \cdot \sin \theta -12=0$，

(1)、 求$\odot C$的参数方程；

分析：将${\rho }^2=x^2+y^2$，$y=\rho \cdot sin\theta$，代入$\odot C$的极坐标方程${\rho }^2-4\rho sin\theta -12=0$，

得到$\odot C$的直角坐标方程为$x^2+y^2-4y-12=0$，即$x^2+(y-2{)}^2=16=4^2$，

故$\odot C$的参数方程为$\{\begin{array}{l}x=4cos\theta \\ y=2+4sin\theta \end{array}$ ($\theta$为参数，$\theta \in [0，2\pi )$)。

(2)、求直线$l$被$\odot C$截得的弦长。

【法1】几何方法，利用$Rt\Delta$求解，将直线$l$的参数方程消参，得到其普通方程为$2x-y-3=0$，

则圆心$(0，2)$到直线的距离为$d=\frac{|-2-3|}{\sqrt{2^2+1^2}}=\sqrt{5}$，

则直线$l$被$\odot C$截得的弦长为$2\sqrt{r^2-d^2}=2\sqrt{4^2-(\sqrt{5}{)}^2}=2\sqrt{11}$。

【法2】弦长公式，设直线和圆的交点为$A(x_1，y_1)，B(x_2，y_2)$，

联立得到方程组，$\{\begin{array}{l}2x-y-3=0\\ x^2+y^2-4y-12=0\end{array}$

消去$y$得到，$x^2+(2x-3{)}^2-4(2x-3)-12=0$，整理得到，$5x^2-20x+9=0$，

由韦达定理得到，$x_1+x_2=4$，$x_1{x}_2=\frac{9}{5}$，

由弦长公式得到，$|AB|=\sqrt{1+k^2}|x_1-x_2|$$=\sqrt{1+2^2}\sqrt{(x_1+x_2{)}^2-4x_1{x}_2}$

$=\sqrt{5}\sqrt{16-\frac{36}{5}}=2\sqrt{11}$。

【法3】利用直线的参数方程求解，需要先判断参数方程是否为标准形式；若不是，还需要转化为标准形式。

直线$l$的参数方程为$\{\begin{array}{l}x=2+t\\ y=1+2t\end{array}(t为参数)$，

(此时千万要注意，弦长$|AB|\ne |t_1-t_2|$，原因是这个参数方程不是标准形式的)

将其做如下的转化，

$\{\begin{array}{l}x=2+\frac{1}{\sqrt{5}}\cdot \sqrt{5}t\\ y=1+\frac{2}{\sqrt{5}}\cdot \sqrt{5}t\end{array}(t为参数)$，

令$\sqrt{5}t=m$，则其参数方程的标准形式为

$\{\begin{array}{l}x=2+\frac{1}{\sqrt{5}}\cdot m\\ y=1+\frac{2}{\sqrt{5}}\cdot m\end{array}(m为参数)$，

[此时参数$m$的几何意义才是动点到定点的距离的数量，千万要注意，即弦长$|AB|=|m_1-m_2|=\sqrt{1^2+2^2}|t_1-t_2|$]

将直线$l$的参数方程的标准形式代入圆的普通方程得到，

$(2+\frac{1}{\sqrt{5}}m{)}^2+(1+\frac{2}{\sqrt{5}}m{)}^2-4(1+\frac{2}{\sqrt{5}}m)-12=0$

整理为$m^2-11=0$，令直线和圆的两个交点$A，B$分别对应的参数为$m_1，m_2$，

则$m_1+m_2=0$，$m_1{m}_2=-11$，

此时弦长$|AB|=|m_1-m_2|=\sqrt{(m_1+m_2{)}^2-4m_1{m}_2}=\sqrt{4\times 11}=2\sqrt{11}$。

或者简单求解如下：

将直线$l$的参数方程$\{\begin{array}{l}x=2+t\\ y=1+2t\end{array}(t为参数)$，代入圆的普通方程$x^2+(y-2{)}^2=4^2$中，

得到 $(2+t{)}^2+(2t-1{)}^2=4^2$，整理得到$5t^2-11=0$，

解得$t_1=-\frac{\sqrt{11}}{\sqrt{5}}$，$t_2=\frac{\sqrt{11}}{\sqrt{5}}$，则$|t_1-t_2|=\frac{2\sqrt{11}}{\sqrt{5}}$

故$|AB|=\sqrt{1^2+2^2}|t_1-t_2|=\sqrt{5}\times \frac{2\sqrt{11}}{\sqrt{5}}=2\sqrt{11}$;

解后反思：

• 非标准形式化为标准形式的思路

$\{\begin{array}{l}x=x_0+at=x_0+\frac{a}{\sqrt{a^2+b^2}}\cdot \sqrt{a^2+b^2}t\\ y=y_0+bt=y_0+\frac{b}{\sqrt{a^2+b^2}}\cdot \sqrt{a^2+b^2}t\end{array}(t为参数)$，

再令$\sqrt{a^2+b^2}t=m$，则得到$\{\begin{array}{l}x=x_0+cos\theta m\\ y=y_0+sin\theta m\end{array}(m为参数)$，这才是标准形式；

此时的参数$m$的几何意义才是定点到动点的有向线段的数量。

【2021届高三文数三轮模拟检测题】已知极坐标系中，曲线 $C$ 的极坐标方程为 $\rho =r(r>4)$，以极点为原点，极轴为 $x$ 轴的非负半轴，建立平面直角坐标系 $xOy$ ，直线 $l$ 的参数方程为 $\{\begin{array}{l}x=4+t\\ y=t\end{array}$ ($t$ 为参数) .

(1). 求曲线 $C$ 的参数方程以及直线 $l$ 的极坐标方程.

解析：由 $\rho =r$，得到 ${\rho }^2=r^2$，则其普通方程为 $x^2+y^2=r^2$ ，

则其参数方程为 $\{\begin{array}{l}x=r\cos \theta \\ y=r\sin \theta \end{array}$ ($\theta$ 为参数) .

直线 $l$ 的参数方程消参后得到，$x-y=4$，将 $x=\rho \cos \theta$， $y=\rho \sin \theta$代入

得到 $\rho \cos \theta -\rho \sin \theta =4$，整理得到 $\rho \cos (\theta +\frac{\pi }{4})=2\sqrt{2}$，

即直线 $l$ 的极坐标方程为 $\rho \cos (\theta +\frac{\pi }{4})=2\sqrt{2}$ .

(2). 若点 $M(4,0)$，直线 $l$ 与曲线 $C$ 交于 $P$、 $Q$ 两点，且 $\frac{1}{|MP|}-\frac{1}{|MQ|}=\sqrt{2}$，求 $r$ 的值.

解析：将 直线 $l$ 的参数方程化为标准形式， $\{\begin{array}{l}x=4+\frac{\sqrt{2}}{2}n\\ y=\frac{\sqrt{2}}{2}n\end{array}$ ($n$ 为参数，且 $n=\sqrt{2}t$) .

将其代入曲线 $C$ 的普通方程 $x^2+y^2=r^2$中 ，整理得到 $n^2+4\sqrt{2}n+16-r^2=0$，

由于$r>4$，故$\Delta =(4\sqrt{2}{)}^2-4(16-r^2)>0$，

设点 $P$、 $Q$ 对应的参数分别为 $n_1$，$n_2$，则由韦达定理可得，

$n_1+n_2=-4\sqrt{2}<0$，$n_1{n}_2=16-r^2<0$，由于 $\frac{1}{|MP|}-\frac{1}{|MQ|}=\sqrt{2}$，

则 $|MP|<|MQ|$，即 $|MP|=|n_1|=n_1>0$， $|MQ|=|n_2|=n_2<0$，

$\frac{1}{|MP|}-\frac{1}{|MQ|}=\frac{|MQ|-|MP|}{|MP||MQ|}=\frac{-n_2-n_1}{|n_1{n}_2|}$

$=\frac{-(n_1+n_2)}{r^2-16}=\frac{4\sqrt{2}}{r^2-16}=\sqrt{2}$，

解得，$r=2\sqrt{5}$(舍去负值)，故$r=2\sqrt{5}$.