手写的高棉数字识别

手写识别 (Handwriting recognition)

Handwriting recognition is a task in categorizing given handwriting patterns into groups (categories). There are many methods to implement this task from a traditional machine learning approach to deep learning such as a convolutional neural network (CNN).

笔迹识别是将给定的笔迹模式分类为组(类别)的任务。 从传统的机器学习方法到深度学习(例如卷积神经网络(CNN))，有很多方法可以实现此任务。

In this article, we introduce a simple pattern recognition method, a linear discriminant analysis by maximum likelihood estimation for Gaussian. We are using a handwritten Khmer digit recognition task as an example.

在本文中，我们介绍了一种简单的模式识别方法，即通过最大似然估计对高斯进行线性判别分析。 我们以手写高棉语数字识别任务为例。

高棉数字 (Khmer Digit)

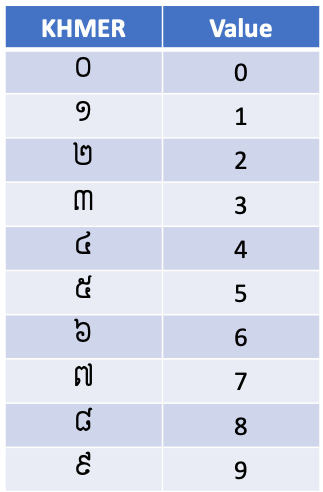
Khmer is the formal language of Cambodia. It is spoken by about 16 million speakers mainly in Cambodia and in a part of Vietnam and Thailand. In the Khmer language, a group of digits shown in Figure 2 is used in the numeral system.

高棉语是柬埔寨的正式语言。 大约有1600万发言人讲这种声音，主要是在柬埔寨以及越南和泰国的部分地区。 在高棉语中，数字系统使用图2所示的一组数字。

Figure 2Khmer digits

图2高棉数字

Figure 3Handwritten Khmer digits

图3手写的高棉数字

线性判别分析(LDA) (Linear Discriminant Analysis (LDA))

Suppose we have samples of pattern x and its category y, {(x_i ,y_i)} (i=1,…,n) where n is the number of the training samples. Let n_y be the number of patterns in the y-category.

假设我们有模式x及其类别y的样本{{x_i，y_i)}(i = 1，…，n)，其中n是训练样本的数量。 令n_y为y类别中的模式数。

To define the corresponding category of a given pattern x, we select a y with the largest value of a posteriori probability p(y|x). Here, p(y|x) is a conditional probability of y given x. This decision rule is called maximum a posteriori probability rule.

为了定义给定模式x的相应类别，我们选择后验概率p(y | x)最大值的ay。 在此，p(y | x)是给定x的y的条件概率。 该决策规则称为最大后验概率规则。

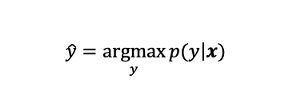
From Bayes’ theory, a posteriori probability can be calculated by

根据贝叶斯理论，可以通过以下公式计算后验概率：

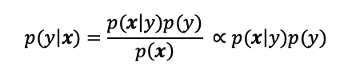
In the above expression, p(x) does not depend on y. Thus, we can ignore the denominator.

在以上表达式中，p(x)不依赖于y。 因此，我们可以忽略分母。

Now we need to estimate p(y) and p(x|y). For y, since it is a discrete probability variable (y is a category), we can simply estimate its probability by the ratio of the number of patterns in y-category to the total number of the samples.

现在我们需要估计p(y)和p(x | y)。 对于y，由于它是离散的概率变量(y是类别)，我们可以简单地通过y类中模式数量与样本总数之比来估计其概率。

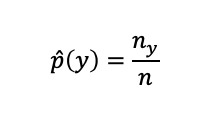
x is a continuous probability variable, we cannot apply the method used with y directly. Here, we will introduce a parametric method.

x是连续概率变量，我们不能直接应用与y一起使用的方法。 在这里，我们将介绍一个参数化方法。

Assuming pattern x is independently and identically distributed by a Gaussian distribution, we will apply maximum likelihood estimation on a Gaussian model to estimate its parameters and calculate the conditional probability p(x|y).

假设模式x由高斯分布独立且相同地分布，我们将对高斯模型应用最大似然估计以估计其参数并计算条件概率p(x | y)。

In general, a Gaussian model of x with d-dimension Gaussian distribution is given by

通常，具有x维高斯分布的x的高斯模型由下式给出：

With maximum likelihood estimation, the estimate of Gaussian model parameters are

对于最大似然估计，高斯模型参数的估计为

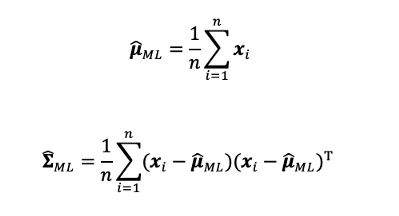
Now the estimate of p(x|y) can be calculated by

现在可以通过下式计算p(x | y)的估计值：

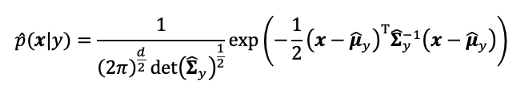
Substituting estimated p(x|y) and p(y) into p(y|x) expression, we can get the posteriori probability of a category y given a pattern x. However, to make it simpler, we use a log function in the following calculation. Since a log function is monotonically increasing, there are no differences between the relationship with p(y|x).

将估计的p(x | y)和p(y)代入p(y | x)表达式中，我们可以得到给定模式x的类别y的后验概率。 但是，为简化起见，我们在以下计算中使用了对数函数。 由于对数函数单调增加，因此与p(y | x)的关系之间没有差异。

To simplify this log-posteriori probability, in linear discriminant analysis, we make the following assumption: the variance-covariance matrix of each category is equal. In this case, the common variance-covariance matrix is

为了简化此对数后验概率，在线性判别分析中，我们做出以下假设：每个类别的方差-协方差矩阵相等。 在这种情况下，公共方差-协方差矩阵为

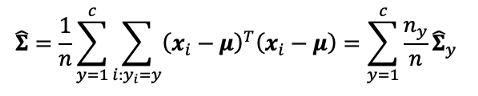
and log p(y|x) is

并且日志p(y | x)是

Therefore, the category y of a given pattern x can be predicted by selecting a y whose log p(y|x) holds the maximum value among all categories.

因此，可以通过在所有类别中选择log p(y | x)保持最大值的ay来预测给定模式x的类别y。

数据集 (Dataset)

Now let’s apply this LDA method on handwritten Khmer digit recognition.

现在让我们将此LDA方法应用于手写高棉数字识别。

In this case, the digital image of the handwritten digit is the pattern x, and0–9 is the category y. We use 1500 of 64x64 grayscaled images as a dataset. We separate this dataset into 1200 for training data and 300 for testing data.

在这种情况下，手写数字的数字图像是模式x，0-9是类别y。 我们使用1500张64x64灰度图像作为数据集。 我们将此数据集分为1200个训练数据和300个测试数据。

For the pattern x, we simply reshape 64x64 grayscaled images to 4096-dimension vectors. Therefore, we applying LDA on a Gaussian model with 4096-dimension Gaussian distribution.

对于模式x，我们只需将64x64灰度图像重塑为4096维矢量。 因此，我们将LDA应用于具有4096维高斯分布的高斯模型。

用Python实现 (Implementation with Python)

o将数据集分为训练和测试集 (o Split dataset into training and testing sets)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

o估计模型的参数(训练) (o Estimate the parameters of the model (training))

means = np.zeros((10, nD*nD))
cov = np.zeros((nD*nD, nD*nD))
count = [sum(map(lambda x : x == i, y_train)) for i in range(0,10)]for i in range(10):
    cov_array = []
    for j in range(len(y_train)):
        if int(y_train[j]) == i:
            means[i] = means[i] + X_train[j]
            cov_array.append(X_train[j])
    cov = cov + np.cov(np.array(cov_array).T) * (count[i]/len(y_train))means = means / len(y_train)
inv_cov = np.linalg.inv(cov + 0.00001*np.eye(nD*nD))

o评估 (o Evaluation)

ans = np.zeros((10, 10),dtype='int')
total = 0
errors = []for i in range(10):
    for j in range(len(y_test)):
        if int(y_test[j]) == i:
            p = np.zeros(10)
            for k in range(len(p)):
                p[k] = np.dot(np.dot(means[k].T, inv_cov), X_test[j]) - (np.dot(np.dot(means[k].T, inv_cov), means[k])) / 2 + np.log(count[i])m = p.argmax()
            if m!=y_test[j]:
                errors.append((j,m))
            ans[m][int(y_test[j])] = int(ans[m][int(y_test[j])] + 1)

码 (Code)

https://github.com/loem-ms/PatternRecognition.git

https://github.com/loem-ms/PatternRecognition.git

结果与讨论 (Result and Discussion)

o混淆矩阵 (o Confusion Matrix)

    0   1   2   3   4   5   6   7   8   90  28   0   0   0   0   0   0   0   0   01   2  27   0   0   0   0   0   0   0   02   0   0  37   0   0   0   0   0   0   03   0   0   0  29   0   0   0   0   0   04   0   0   0   0  33   0   0   0   1   05   0   0   0   0   0  25   0   0   0   06   0   0   0   0   0   0  26   0   0   07   0   0   0   0   0   0   0  28   0   08   0   0   0   0   0   0   0   0  38   09   0   0   0   0   0   0   0   0   0  26

o测试精度 (o Test Accuracy)

0.99

It works!

有用！

o错误情况 (o Error cases)

Category: ១ ; Predict: ០

类别：១； 预测：០

Category: ៤ ; Predict: ​​ ៨

类别：៤； 预测：៨

Different from a black box concept in other deep learning-based methods, using LDA we can simply understand the process of the learning using data’s statistical features.

与其他基于深度学习的方法中的黑盒概念不同，使用LDA，我们可以使用数据的统计特征简单地了解学习过程。

However, since it is a linear-based model, in some case which cannot be recognized by a linear discriminatory function, the performance will drop down noticeably.

但是，由于它是基于线性的模型，因此在某些情况下无法通过线性判别函数识别，因此性能会明显下降。

Another problem is the dimension of input pattern x. In this example, we are using 4096-dimension vectors(64x64) as input and it takes 7.17second(note PC)in estimating the model parameters. When increasing input images to 128x128 which means using 16384-dimension vectors as input, it takes 470.80second. Increasing the dimension of input vectors results in huge time complexity when calculating the inverse matrix of the variance-covariance matrix.

另一个问题是输入模式x的尺寸。 在此示例中，我们使用4096维矢量(64x64)作为输入，估计模型参数需要7.17秒(注意PC)。 将输入图像增加到128x128时，这意味着使用16384维矢量作为输入，这需要470.80秒。 在计算方差-协方差矩阵的逆矩阵时，增加输入矢量的维数会导致巨大的时间复杂度。

翻译自: https://towardsdatascience.com/handwritten-khmer-digit-recognition-860edf06cd57