三元赫尔德不等式_权方和不等式

大家好，我是此意难平。本人浙江高三学生，还处于网络萌新阶段，发现B乎是个学习知识的好地方，第一次写文章，所以(*￣m￣)呃呃呃，都加油啦

那么就进入正题

若

为实数，

,则：

当

时，等号成立。

此式是柯西不等式的推论，称权方和不等式

题目：已知对所有正实数a,b,c。

求证:

emmm乍一看，完全没什么思路

方法1：(原答案）

不妨记x=

y=

z=

那么

=

;

=

;

=

显然有:

所以(

)

假设

，则 显然

那么与假设矛盾，

所以假设

不成立。

因此

成立。命题得证。

方法2 (码字太累了，接下来用图片(~_~;))

函数的凹凸性以及琴生不等式

关于函数的凹凸性以及琴生不等式

知之子：函数的凹凸性漫谈｜高等数学漫步（二）​zhuanlan.zhihu.com

JetfiRex：不等式(4) - 琴生不等式和优超不等式​zhuanlan.zhihu.com

方法3：当然就是权方和不等式了( ´͈ ᵕ `͈ )◞♡

如果有其他的方法，欢迎补充

补充：感谢Old Zhang 提供另解

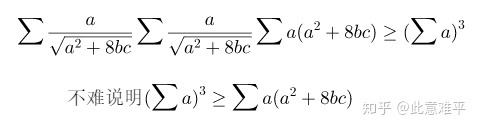
2020 4.9

之后会陆续的加一些例题，争取在开学前完成

关于评论补充

解题利器：权方和不等式及其应用​www.360doc.com

---

补充一下

从笔记里找了一些例题，如下

例2.0已知

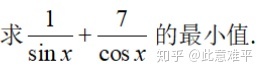
PS:其实是用赫尔德不等式

例2.1

总结：重点是分子的幂指数比分母高一次（敲黑板）

例3.

例题4.

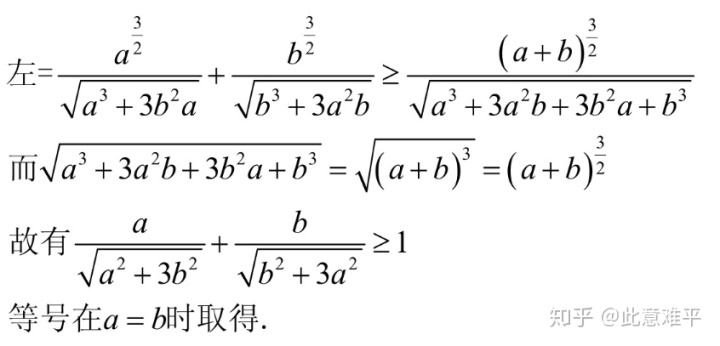
同时本题的三元形式就是例题1

例题5.

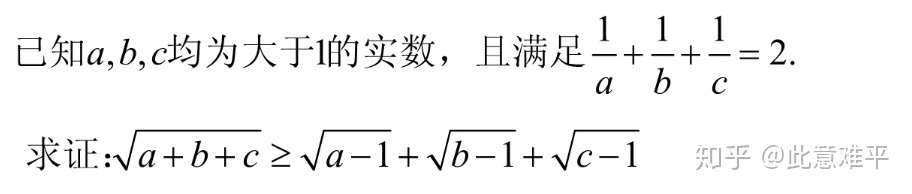
最后再来一题

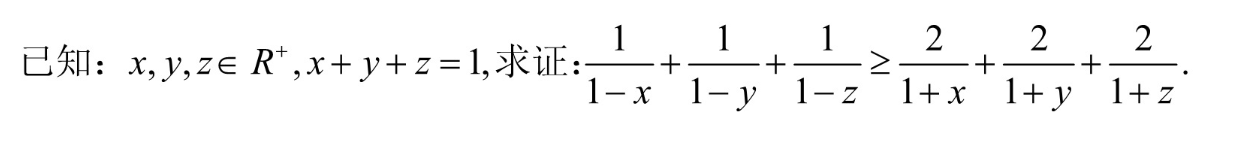
同时累加3式得到（当

)

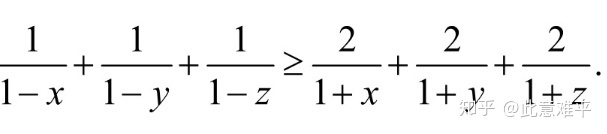
差不多就这样了emmmm

总结：

1. 如果细心的话，你们可能已经发现了，加权不等式核心就是权（未知式），而当它们地位相等时最小（x=y=z）（什么叫地位相等~(￣▽￣)~*，就是把x换做y形式也等价）
2. 它可以避免繁复的计算，小巧玲珑，可能这就是数学的美吧

可能讲的不清楚（仅为个人理解），

请多包涵

开学前，争取再写一篇关于极线的运用的例子
2020 /4.09 /21.33

---

PS:发现在专栏上的不等式例题很少，所以emmm

1. 希望对各位小可爱有帮助

柯西不等式

柯西不等式​mp.weixin.qq.com

赫尔德不等式

赫尔德不等式​mp.weixin.qq.com

n元基本不等式

n元基本不等式1​mp.weixin.qq.com n元基本不等式2​mp.weixin.qq.com

Aczel不等式

Aczel不等式​mp.weixin.qq.com

Aczel-闵科夫斯基不等式

Aczel-闵科夫斯基不等式​mp.weixin.qq.com